Бернулли теңдеуі.

нақты саны үшін

(9.14 )

түрінде берілген теңдеу Бернулли теңдеуі деп аталады, мұндағы - берілген үзіліссіз функциялар және .

Бернулли теңдеуін шешу үшін алмастыру арқылы сызықтық теңдеуге келтіруге болады, яғни (9.14) теңдеудің екі жағын да деп, шамасына көбейтеміз, сонда:

теңдеуінде деп, белгілеуін енгіземіз. Сонда . Демек, Бернулли теңдеуі осы функцияға қатысты сызықты дифференциалдық теңдеуге келтіріледі: . Бұл - ке қатысты сызықты дифференциалдық теңдеу, оны шешіп, функциясын тауып, белгілеуін ескеріп, белгісіз шешімін табамыз.

Толық дифференциалдық теңдеу.

Теорема. және функциялары бір байланысты D облысында бірінші ретті дербес туындыларымен қоса үзіліссіз функциялар болсын. Онда

(9.15)

дифференциалдық өрнегі кейбір функциясының толық дифференциалы болуы үшін, нүктесі үшін

(9.16)

шартының орындалуы қажетті және жеткілікті.

Дәлелдеуі. Қажеттілігі. өрнек функциясының толық дифференциалы болсын:

. (9.17)

Онда теңдігін ескерсек, бұдан

, (9.18)

теңдіктерін аламыз. (9.18) теңдіктерін сәйкесінше у және х бойынша дифференциалдап,

аламыз. Ал, аралас туындылар және өзара тең, онда (9.16) теңдікті аламыз, яғни .

Жеткіліктілігі. (9.16) шарт орындалсын. (9.15) дифференциалдық өрнек кейбір функциясының дифференциалы болатындай, функциясын табайық. Онда толық дифференциалдың анықтамасы бойынша (9.17), (9.18) теңдіктерін алып, (9.18) теңдіктердің біріншісін х бойынша интегралдасақ:

, (9.19)

мұнда ерікті тұрақты ретінде у - тен тәуелді дифференциалданатын функциясын аламыз. (9.18) теңдіктердің екіншісін ескере отырып, (9.19) теңдіктің екі жағын у бойынша дифференциалдасақ,

. (9.20)

Табылған функциясын (9.19) теңдікке апарып қойсақ,

ізделіп отырған функцияны аламыз. Теорема дәлелденді.

Сонымен, теңдік өрнек функциясының толық дифференциалы болу шарты деп аталады. Ал, сәйкес

(9.21)

теңдеу, толық дифференциалдық теңдеу деп аталады. Ендеше, өрнегі бұл теңдеудің жалпы интегралы деп аталады.

Егер болса, онда толық дифференциалдық теңдеу емес. Онда демеушілік көбейткіш функциясына берілген теңдеудің екі жағын да көбейту арқылы теңдеуді толық дифференциалдық теңдеуге келтіреміз. Бұл кезде (9.16) шарт мына түрге келеді:

. (9.22)

Бұл теңдеуді шешу қиынырақ, тек кейбір жағдайларын қарастырамыз.

а) - х –тен тәуелді функция болсын. Онда болады.

(9.22) теңдеу мына түрге келеді:

. (9.23)

(9.23) теңдікте өрнегі х – ке тәуелді болса, онда ол теңдеу айнымалылары ажыратылатын теңдеуге келеді, оның шешімі:

.

б) - у –тен тәуелді функция болсын. Онда болады.

(9.22) теңдеу мына түрге келеді:

. (9.24)

(9.24) теңдікте өрнегі у – ке тәуелді болса, онда ол теңдеу айнымалылары ажыратылатын теңдеуге келеді, оның шешімі:

.

Мысалдар. 1. теңдеуін Бернулли тәсілімен шешіңіз.

Шешуі. , , сонда , яғни . Алдымен теңдеуін шешеміз:

. Енді , . Сонымен, берілген теңдеудің жалпы шешімі , яғни .

2. теңдеуін Лагранж тәсілімен шешіңіз.

Шешуі. біртекті сызықты дифференциалдық теңдеуді шешеміз. . С – ны С(х) функциясына ауыстырамыз, яғни берілген теңдеудің шешімін түрінде іздейміз, . Сонда немесе , интегралдасақ . Сондықтан, - берілген теңдеудің жалпы шешімі.

3. теңдеуін демеушілік көбейткіш тәсілімен шешіңіз.

Шешуі. - демеушілік көбейткішті анықтаймыз: , яғни . Берілген теңдеуді көбейтеміз: . Теңдеудің сол жағы , интегралдасақ,

- берілген теңдеудің жалпы интегралы.

4. теңдеуін шешіңіз.

Шешуі. Бернулли теңдеуі берілген: . Бұл теңдеудің екі жағын у – ке көбейтеміз, сонда . белгілеуін енгізіп, аламыз. Демек, Бернулли теңдеуі - ке қатысты сызықты дифференциалдық теңдеуге келді: , . Бұл теңдеуді Бернулли тәсілімен шешейік: , , сонда , яғни . Алдымен теңдеуін шешеміз: .

Енді , . Бұдан , белгілеуін ескеріп, - берілген теңдеудің жалпы шешімі.

5. теңдеуін шешіңіз.

Шешуі. , . Берілген теңдеу толық дифференциалдық теңдеу болады, себебі , , яғни . Белгісіз функцияны арқылы белгілесек, онда , . Бірінші қатынастан: ; ; . Екінші қатынастан: , екінші жағынан . Алынған өрнектерді салыстырып, айнымалылары ажыратылатын теңдеу аламыз: . Интегралдасақ, , бұл мәнді теңдеуінің орнына қойсақ, . Ендеше, берілген теңдеудің жалпы шешімі: .

6. теңдеуін шешіңіз.

Шешуі. , , , , . Ендеше, берілген теңдеу толық дифференциалдық теңдеу болмайды, бірақ 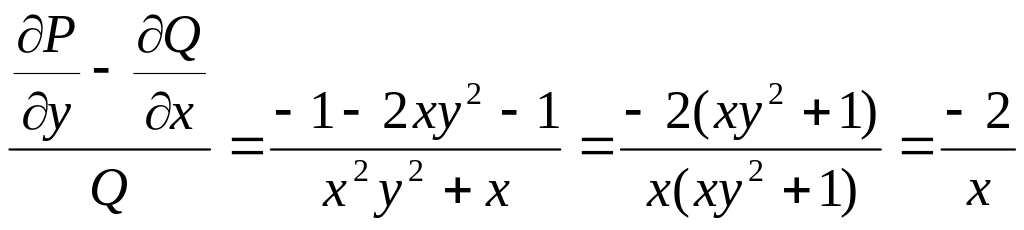теңдеуі х – тен ғана тәуелді, онда теңдеудің х –тен тәуелді демеушілік көбейткіші болады. формуласы бойынша С₁=1 десек, . Берілген теңдеуді көбейтсек,

, яғни теңдеу толық дифференциалдық теңдеуге келтіріледі. Оны шешсек, берілген теңдеудің жалпы шешімі мына түрде болады: .

Жоғарғы ретті дифференциалдық теңдеулер

Жалпы түсінік. Коши есебі.

Берілген

(9.1)

немесе ең жоғарғы туындысы арқылы шешілген

(9.2)

теңдеулер n – ші ретті дифференциалдық теңдеу деп аталады. n – ші ретті дифференциалдық теңдеудің жалпы шешімі n ерікті интегралдық тұрақтыдан тәуелді, яғни

(9.25)

n рет үзіліссіз дифференциалданатын функция болады. Ендеше, (9.1) немесе (9.2) дифференциалдық теңдеулердің жалпы интегралы

(9.26)

теңдігімен анықталады.

Геометриялық тұрғыдан қарасақ, берілген n – ші ретті дифференциалдық теңдеулердің жалпы шешімі Оху жазықтығында жатқан n ерікті интегралдық тұрақтыдан тәуелді қисықтар жиынтығын береді. Солардың ішінен біреуін бөліп алу, яғни оның дербес шешімін алу үшін, осы тұрақтыларды анықтайтын теңдеуден басқа қосымша шарт берілуі керек. Ол шарт (9.25) функциясының және (n-1) – ші ретті туындыларының аралығында жататын х=x₀ нүктесіндегі мәндері:

_{, (9.27)}

мұндағы алдын ала берілген сандар. Берілген (9.27) теңдіктер бастапқы шарттар немесе Коши шарттары деп аталады. Оларды қолдану арқылы (9.1) немесе (9.2) дифференциалдық теңдеудің дербес шешімін табу Коши есебін шешу деп аталады.

Теорема (Коши есебі шешімінің бар және оның жалғыз болуы жөнінде). (9.1) немесе (9.2) дифференциалдық теңдеу және (9.27) бастапқы шарттар берілсін. Егер функциясы нүктесінің белгілі бір маңайында үзіліссіз және үзіліссіз дербес туындылары болса, онда ол дифференциалдық теңдеудің х₀ нүктесінің белгілі бір маңайында анықталған және берілген бастапқы шарттарды қанағаттандыратын шешімі бар және ол шешім жалғыз болады.