Примеры решения задач 

1. На заряд Q = 16ּ10 ^–8 Кл действует сила F = 2,4ּ10 ^–3 Н. Найти напряженность электрического поля в данной точке. Определить заряд Q₀, создающей это поле, если он удален от этой точки на расстояние r = 0,3 м в вакууме.

Дано: Q = 16ּ10–8 Кл F = 2,4ּ10 –3 Н r = 0,3 м	Решение Напряженность поля в данной точке: Е = F / Q = 2,4ּ10 –3/ (16ּ10 –8) = 0,15ּ10 5 В/м Значение заряда при данной напряженности: Q0 = Е4nεε0r2 = 0,15ּ105ּ4ּ3,14ּ8,85ּ10-12ּ(0,3)2 = = 15ּ10 –8 Кл. Ответ: 0,15ּ10 5 В/м; 15ּ10 –8 Кл.
E, Q0 – ?

2. Два разнополярных заряда в стекле Q₁ = + 3,5ּ10 ^-9 Кл и Q₂ = -3,5ּ10^-9 Кл находятся на расстоянии r = l8 cм друг от друга. Заряд Q₃ = + 2ּ10^-8 Кл расположен на расстоянии r = 24 см от этих двух зарядов. Определить значение и направ­ление напряженности поля Е в точке, находящейся посередине между зарядами Q₁ и Q₂.

Дано: Q1 = + 3,5ּ10 -9 Кл Q2 = -3,5ּ10-9 Кл r = l8 cм Q3 = + 2ּ10-8 Кл r = 24 м	Решение Напряженность поля от действия заряда Q1 в искомой точке: Е1 = 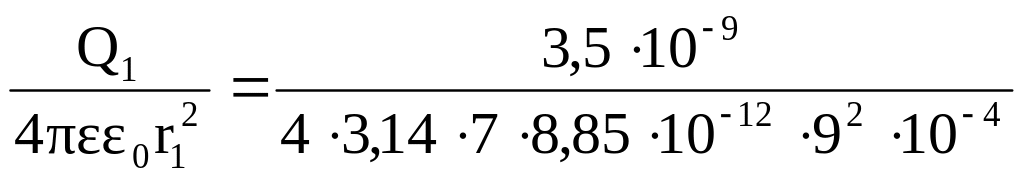= 550 В/м. Напряженность Е2 = 550 В/м, так как Q1 = Q2 и r1 = r1. Для определения напряженности в этой же точке от действия заряда Q3 необходимо найти расстояние r3 этой точки от заряда Q3: из прямоугольного треугольника имеем r3 = = 22,2 см.
E – ?

3. Найдем напряженность Е₃:

Е₃ = = 520 В/м.

4. Определим вектор напряженности поля в указанной точке: Е = Е₁ + Е₂ + Е₃.

Векторы Е₁ и Е₂ направлены в одну сторону (так как заряды Q₁ и Q₂ разноименные и Е₁₂ = Е₁ + Е₂ = 550 + 550 = 1100 В/м.

Вектор Е₃ направлен перпендикулярно вектору Е₁₂, и суммарный вектор напряженности:

E = = 1220 В/м.

При определении направления вектора Е необ­ходимо помнить, что оно совпадает с направлением силы, действующей на положительный заряд.

Ответ: 1220 В/м.

3. К выводам плоского воздушного конден­сатора приложено напряжение U = 800 В. Определить напряженность электрического поля конденсатора при расстоянии между пластинами d = 5 мм и силу, действующую в этом поле на единичный заряд Q = 1,5ּ10^-7 Кл. Определить емкость конденсатора, если площадь каждой пластины S = 24 см². Как изменится его емкость, если конденсатор поместить в спирт?

Дано: U = 800 В d = 5 мм Q = 1,5ּ10-7 Кл S = 24 см2	Решение Напряженность электрического поля плоского конденсатора Е = U / d = 800 / (5ּ10-3) = 16ּ104, В/м Если заряд помещен в электрическое поле конденсатора, то F = EQ = 16ּ104ּ1,5ּ10-7 = 0,024 Н. Емкость плоского воздушного конденсатора С = = 4,25ּ10-12 Ф = 4,25 пФ.
C' – ?

Если конденсатор помещен в спирт, диэлект­рическая проницаемость которого

ε = 33, емкость увеличивается в 33 раза при неизменных расстоянии между

пластинами и площади пластин:

С' = С ε = 4,25 пФ ּ33 = 140 пФ.

Ответ: 140 пФ.

4. Два плоских конденсатора емкостями С1 = 0,5 мкФ и С2 = 1,5 мкФ соединены последовате­льно и подключены к источнику питания. При этом на обкладках конденсаторов появился заряд Q = 4,5ּ10^-4 Кл. Оба конденсатора имеют одинако­вые площади пластин и одинаковый диэлектрик. Определить общую (эквивалентную) емкость соедине­ния, подведенное напряжение, падение напряжения на обоих конденсаторах и расстояние между пла­стинами первого конденсатора, если напряженность электрического поля второго конденсатора Е = 2000 В/см. Определить энергию электрического поля эквивалентного конденсатора.

Дано: С1 = 0,5 мкФ С2 = 1,5 мкФ Q = 4,5ּ10-4 Кл Е = 2000 В/см

Решение Определим напряжения U1 и U2, на конденсаторах: U1 = Q / C1 = 4,5ּ10-4 / (0,5ּ10-6) = 900 В; U2 = Q / C2 = 4,5ּ10-4 / (1,5ּ10-6) = 300 В. Напряжение, подведенное к зажимам цепи U = U1 + U2 = 900 + 300 = 1200 В. Общая, или эквивалентная, емкость последовате­льно соединенных конденсаторов C = C1C2 / (C1 + C2) = 0,5ּl,5 / (0,5 + l,5) = 0,375 мкФ, или С = Q / U = 4,5ּ10-4 / 1200 = 0,375ּ10-6 Ф = 0,375 мкФ.

С, U, d1, W – ?

4. Определим расстояние между пластинами второго конденсатора по (1.9):

d₂ = U₂ / E =300 / 2000 = 0,15 см.

5. Если конденсаторы имеют одинаковые площади пластин и один и тот же диэлектрик, то С₁ / С₂ = d₂ / d₁,

откуда d₁ = = 0,45 см.

6. Энергию электрического поля найдем по (1.12)

W = CU² / 2 = 0,375ּ10^-6ּ1200² / 2 = 0,29 Дж.

Ответ: 0,375 мкФ, 1200В, 0,45см, 0,29 Дж.

Контрольные вопросы 

1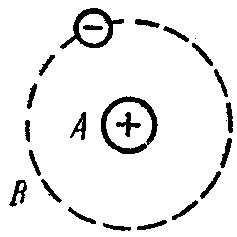 . На рисунке показана модель атома водорода. В какой области пространства действует электрическое поле

а) в области А;

б) в области В?

2. Какое из приведённых утверждений вы считаете правильным?

а) поле и силовые линии существуют реально;

б) поле существует реально, а силовые линии условно;

в) поле и силовые линии существуют условно.

3. Какой величиной является потенциал электрического поля?

а) векторной;

б) скалярной.

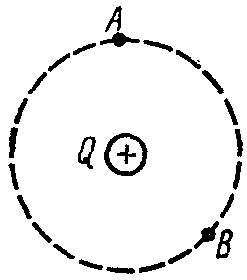
4. Какого соотношение между потенциалами точек А и В?

а) V_A = V_B;

б) V_A  V_B.

5. При параллельном соединении трёх конденсаторов, подключенных к источнику питания, один из них (С₃) оказался пробитым. Как изменится напряжение на конденсаторах и какой станет их общая ёмкость?

а) U = const; С_общ = С₁ +С₂;

б) U = 0; С_общ = .

6. Три конденсатора подключенные к источнику питания, соединены последовательно. Как будет распределяться напряжение на конденсаторах?

а) U₁ > U₂ > U₃;

б) U₃ > U₂ > U₁;

в) недостаточно данных для ответа на вопрос.

7.Три конденсатора можно соединить последовательно, параллельно и по схемам смешанного соединения. Сколько схем соединения можно построить из трех конденсаторов одинаковой емкости С и какая из них имеет наименьшую эквивалентную емкость?

Задачи для самостоятельного решения 

1. Два заряда Q₁ = 5ּ10^-8 Кл и Q₂ = 12ּ10^-8 Кл, находящиеся на расстоянии r = 20 см друг от друга, разделены диэлектриком, в качестве которого использована парафинированная бумага. Определить силу взаимодействия этих за­рядов. Как она изменится, если убрать диэлектрик?

2. Определить силу взаимодействия двух заря­дов Q = 3,5ּ10^-7 Кл и Q₂ = 6ּ10^-7 Кл, находящихся на расстоянии r = 5 см друг от друга и помещенных в воду.

3. Два заряда Q₁ и Q₂, находящиеся на рас­стоянии r = 10 см в воздухе, взаимодействуют с силой F = 1,2 H. Определить заряд Q₂, если известно, что Q₁ = 6ּ10^-7 Кл.

4. Между двумя зарядами Q₁ = 22ּ10^-7 Кл и Q₂ = 5ּ10^-7 Кл помещен электрокартон. Сила взаимодействия этих зарядов F = 0,8 H. Определить расстояние между ними.

   5. Два заряда Q₁ и Q₂, находящиеся на расстоянии r = 25 см в воздухе, взаимодействуют с силой F = 0,l H. Определить заряд Q₂, если Q = l,5ּ10^-6 Кл.

   6. Сила взаимодействия двух зарядов, нахо­дящихся в воздухе, F = 3 Н; Q₁ = 3ּ10^-5 Кл и Q₂ = 0,6ּ10^-5 Кл. Определить расстояние между ними.

   7. Определить напряженность электрического поля, действующего с силой F = 5,4ּ10^-4 Н на заряд Q = 1,8ּ10^-3 Кл.

   8. Электрическое поле с напряженностью Е = 0,8 В/м действует на заряд с силой F = 9,6ּ10^-4 Н. Определить этот заряд.

   9. Определить силу, с которой действует элек­трическое поле, имеющее напряженность Е = 1,4 В/м, на заряд Q = 4ּ10^-6 Кл.

   10. На расстоянии r = 1,5 см от заряда Q, на­ходящегося в воздухе, напряженность электрического поля Е = 650 кВ/м. Определить заряд Q.

   11. Определить заряд, перемещенный в точку поля с потенциалом φ = 10В, если при этом совер­шена работа А = 0,5ּ10^-6 Дж.

   12. Потенциал электрического поля φ = 20 В. Определить работу, совершаемую силами этого поля, при внесении в него заряда Q = 5,5ּ10^-4 Кл.

   13. Напряженность электрического поля Е = 5ּ10^-2 В/м. Определить силу, с которой дей­ствует это поле на заряд Q = 1,6ּ10^-3 Кл, и работу по перемещению этого заряда в точку поля с потен­циалом φ = 45 В.

   14. Определить разность потенциалов между двумя точками электрического поля, если при перемещении заряда Q = 0,5ּ10^-6 Кл совершена работа А = 18ּ10^-5 Дж.

   15. Определить емкость конденсатора, если он был заряжен до напряжения U = 250 В. При этом заряд конденсатора Q = l0^-4 Кл.

   16. Определить напряженность электрического поля между пластинами плоского конденсатора, находящимися на расстоянии d = 3 мм, если напряже­ние, приложенное к ним, U = 450 В. Определить емкость этого конденсатора при условии, что заряд на его пластинах Q = 3ּ10^-4 Kл.

   17. Плоский воздушный конденсатор емкостью С = 1мкФ заряжен от источника постоянного тока напряжением 27 В. Определить заряд и напряжен­ность электричес-кого поля заряженного конденсатора при расстоянии между его пластинами d = 1,5 мм. Определить также энергию электрического поля.

   18. Емкость конденсатора С = 1,5 мкФ, заряд на его обкладках Q = 45ּ10^-5 Кл. Определить напряже­ние на зажимах конденсатора.

   19. Конденсатор заряжен от источника питания напряжением U = 100 В. Энергия электрического поля конденсатора W = 6·10^-3 Дж. Определить его ем­кость.

   20. К конденсатору емкостью С = 0,25 мкФ под­ведено напряжение U = 400 В. Определить энергию электрического поля конденсатора.

   21. Определить эквивалентную (общую) емкость С двух последовательно включенных конденсаторов С1 = С2 = 0,7 мкФ.

   22. Общая емкость двух последовательно вклю­ченных конденсаторов С = 1,2 мкФ. Емкость одного конденсатора С1 = 3 мкФ. Определить емкость второ­го конденсатора.

   23. Конденсаторы емкостями С1 = 10 мкФ и С2 = 15 мкФ соединены последовательно. Опреде­лить их эквивалентную емкость.

   24. Три конденсатора одинаковой емкости С1 = С2 = СЗ = 12 мкФ соединены последо-вательно. Определить их эквивалентную емкость.

   25. Общая емкость трех последовательно со­единенных конденсаторов С = 0,08 мкФ. Определить емкость одного из конденсаторов, если емкости С1 = 0,2 мкФ, С2 = 0,4 мкФ. Определить их эквива­лентную емкость при параллельном соединении конденсаторов.

   26. Четыре конденсатора емкостями С7 = 0,18 мкФ, С2 = 0,7 мкФ, C3 = 0,12 мкФ и С4 = 0,5 мкФ соединены параллельно. Определить их эквивалентную емкость.

   27. Три конденсатора емкостями С1 = 47 пФ, С2 = 18 пФ, С3 = 75 пФ соединены параллельно, и к ним последовательно подключен конденсатор С4 = 75 пФ. Определить общую емкость цепи и эк­вивалентную емкость конденсаторов, если конден­сатор С4 подсоединить параллельно.

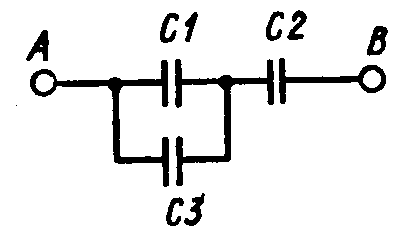
   28. На рис. представлена схема соединения конденсаторов, где С1 = С2 = 1 мкФ, С3 = 2 мкФ. Определить эквивалентную ем­кость.

5. Общая емкость двух последовательно со­единенных конденсаторов С_об = 18 мкФ. Определить емкость каждого конденсатора, если напряжение на зажимах цепи U = 450 В, а на конденсаторе С1 U₁ = 150 В.