2. Электрическое поле

1. Основные свойства и характеристики электрического поля …………………. 13

2. Проводники и диэлектрики в электрическом поле …………………………… 17

3. Электрическая емкость. Конденсаторы ………………………………………… 22

Основные формулы …………………………………………………………… 26

Обозначения ……………………………………………………………………. 27

Примеры решения задач ……………………………………………………… 28

Контрольные вопросы ………………………………………………………… 30

Задачи для самостоятельного решения ………………………………….….. 31

Представление об электрическом поле сложилось в результате изучения электрических явлений — притяжения и отталкивания наэлектризованных тел, электростатической индукции и др.

Большие заслуги в этом принадлежат родоначальнику русской науки М. В. Ломоносову, который вместе с Г. В. Рихманом проводил количественные исследования атмосферного электричества.

1. Основные свойства и характеристики электрического поля

Электрическое поле обнаруживается в пространстве, окружающем заряженные частицы и тела, с которыми это поле связано.

Главным свойством электрического поля является силовое действие на электрически заряженную частицу, причем сила воздействия пропорциональна заряду частицы и не зависит от ее скорости.

Электрическое поле неподвижных заряженных тел при отсутствии в них электрических токов называется электростатическим.

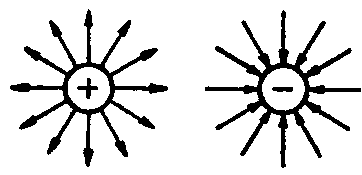
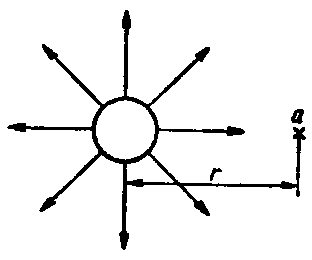
Закон Кулона. В результате опытов французский физик Кулон в 1785 г. установил закон, выражающий силу взаимодействия двух наэлектризованных тел (рис.2.1).

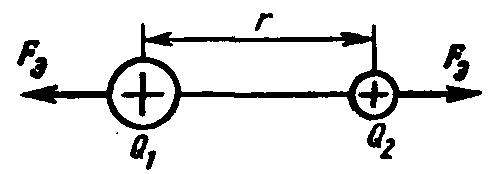
Рис. 2.1

Далее формулировка и математическое выражение закона Кулона приведены для случая взаимодействия точечных заряженных тел, т. е. тел, линейные размеры которых бесконечно малы.

Сила взаимодействия двух точечных заряженных тел прямо пропорциональна произведению зарядов этих тел и обратно пропорциональна квадрату расстояния между ними:

, ( 2.1)

где F_э — электрическая сила, Н (ньютон); Q₁, Q₂ — электрические заряды, Кл (кулон); r — расстояние между заряженными телами, м (метр); ₀ = 8,8510^-12 Ф/м (фарад/метр) —электрическая постоянная, величина, которая определяется выбором системы единиц.

Электрическое поле создается заряженными частицами и телами и вместе с тем действует на заряженные частицы и тела с некоторой силой. Учитывая это, отметим два важных обстоятельства: каждое из двух взаимодействующих тел (с зарядами Q₁ и Q₂) создает свое электрическое поле, а в окружающем их пространстве одно поле накладывается на другое и образуется общее электрическое поле (в данном случае действует принцип наложения полей); силовое взаимодействие двух заряженных тел следует рассматривать как результат действия на каждое из них общего электрического поля, созданного этими телами.

Напряженность электрического поля.

Силовой характеристикой электрического поля является напряженность электрического поля.

Напряженность электрического поля — векторная величина, численно равная отношению силы, действующей на положительно заряженную частицу, к ее заряду:

Е = F_э / Q₂ , (2.2)

где Е — напряженность электрического поля, В/м (вольт/метр). Разделив обе части формулы (2.1) на Q₂, получим выражение напряженности электрического поля точечного заряженного тела и в любой точке, отстоящей от него на расстоянии r:

Е = Q / (4₀ r²). (2.3)

Для наглядного изображения электрического поля проводят линии напряженности (силовые линии). В каждой точке такой линии направление вектора напряженности электрического поля совпадает с касательной к этой линии (рис. 2.2, а – г).

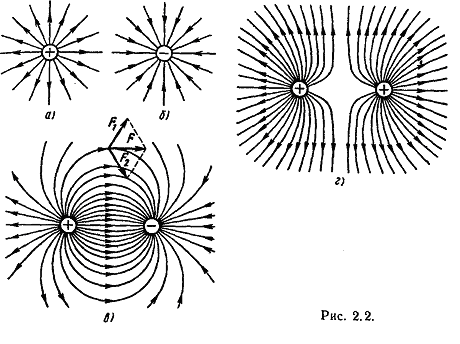
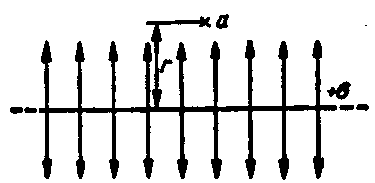
Электрическое поле называют однородным (или равномерным), если во всех его точках напряженность поля одинакова по величине и направлению.

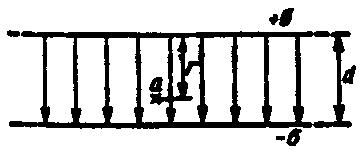
Равномерное поле имеется между двумя параллельными заряженными пластинами, линейные размеры которых значительно больше расстояния между ними (рис. 2.9, а), а у краев пластин поле неравномерно.

Электрическое напряжение. Свободная частица с положительным зарядом Q в электрическом поле будет перемещаться в направлении действующей на нее электрической силы F_э.

Рис. 2.3

При перемещении частицы на расстояние l между точками 1 и 2 совершается работа А_1.2 = f_э l , которую можно выразить через напряженность электрического поля, учитывая формулу (2.2):

А_1.2 = Е Q l.

Работа зависит не только от величин, относящихся к полю (Е, l), но и от заряда частицы Q. Поэтому энергетической характеристикой электрического поля служит не сама величина работы, а отношение ее к величине заряда перемещенной частицы:

U = A_1.2 /Q , (2.4)

U – электрическое напряжение, В (вольт);

A_1.2 – работа, Дж (джоуль).

Отношение работы сил электрического поля по перемещению заряженной частицы между двумя точками к величине заряда частицы называется электрическим напряжением между этими точками.

В равенство (2.4) подставим выражение работы, получим формулу, в которой энергетическая характеристика электрического поля (U) связана с силовой характеристикой (Е):

U = Е l. (2.5)

Для расчета применяется также энергетическая характеристика электрического поля в каждой точке — электрический потенциал (V). Предположим, что пробная частица, обладающая зарядом Q, расположена в точке 1. Частица обладает потенциальной энергией A₁.

Отношение потенциальной энергии заряженной частицы, находящейся в некоторой точке электрического поля, к величине ее заряда выражает потенциал поля в этой точке: V₁ = А₁ /Q; V₂ = А₂ / Q.

Потенциальная энергия заряженной частицы в электрическом поле уменьшается при переходе от точки к точке по направлению линий напряженности. Она становится равной нулю за пределами электрического поля, где сила F_э = 0.

При перемещении заряженной частицы из точки 1 в точку 2 под действием силы F_э, совершается работа А_1.2. На эту величину потенциальная энергия частицы в точке 2 меньше, чем в точке 1: А_1.2 = А₁ – А₂. Разделив это выражение на величину заряда, получим U_1.2 = A_1.2 / Q = A₁ / Q – A₂ / Q или

U_1.2 = V₁ – V₂. (2.6)

Обычно потенциальную энергию и потенциал определяют относительно какого-либо уровня, принятого за начальный.

При решении практических задач, относящихся к электрическим установкам, начальным обычно полагают потенциал земли, который принимают равным нулю.

Определение характеристик электрического поля. Определение напряженности электрического поля, потенциалов, напряжений является одной из задач расчета электрических полей.

Напряженность электрического поля уединенного точечного заряженного тела в любой точке определяют по формуле (2.3), используя которую можно получить выражение для определения величины потенциала.

В практике чаще встречаются случаи, когда заряд тела распределен по его поверхности с некоторой плотностью. Расчет электрических полей в этих случаях осуществляется по формулам, которые получены на основе теоремы Гаусса, и приведены в табл. 2.1 без доказательств.

Таблица 2.1

Заряженное тело, образующее электрическое поле	Напряженность электрического поля	Потенциал	Величины, входящие в формулы
Уединенное точечное тело	Е =	V =	Q – заряд (Кл);  = Q / S – поверхностная плотность (Кл/м2);  – линейная плотность заряда (Кл/м); r – расстояние от положи-тельной пластины, от центра сферы, от оси про-вода до данной точки (м); rх – расстояние от центра сферы, от оси провода до точки, потенциал которой равен нулю (Vх = 0); R – радиус сферы (м); d – расстояние между плас-тинами (м); l – длина провода (м).
Плоскость бесконечной протяженности	Е =	V = (rх – r)
Две параллельные плоскости	Е =	V = (d – r)
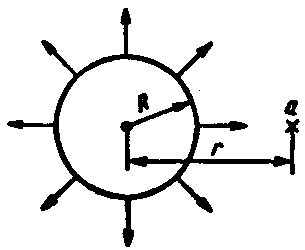
Сфера	Е = = =	V = = =
Прямой провод бесконечной длины	Е = = =	V =