5. Однофазные электрические цепи переменного тока

1. Векторные диаграммы, их обоснование. Активное, индуктивное

и ёмкостное сопротивления в цепи переменного тока. Сдвиг фаз между

током и напряжением……………………………………………………………….. 70

2. Последовательное соединение (неразветвленная цепь) с активными

и реактивными элементами ………………………………………………………… 72

3. Треугольники сопротивлений, мощностей ……………………………………….. 73

4. Разветвленная цепь (параллельное соединение) с активными и

реактивными элементами …………………………………………………………. 73

5. Резонанс токов и напряжений в цепях переменного тока………………………... 74

6. Коэффициент мощности, его значение и способы повышения………………….. 75

Основные формулы……………………………………………………….. 76

Обозначения……………………………………………………………….. 77

Примеры решения задач …………………………………………………. 78

Контрольные вопросы…………………………………………………….. 80

Задачи для самостоятельного решения………………………………….. 80

1. Векторные диаграммы, их обоснование. Активное, индуктивное и емкостное сопротивления в цепи переменного тока. Сдвиг фаз между током и напряжением.

Электрический ток, изменяющийся с течением времени, называют переменным током.

Ц

епь с активным сопротивлением.

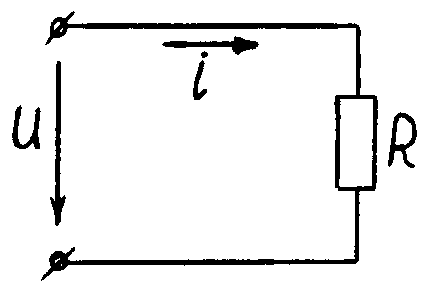
На зажимах цепи переменного тока действует напряжение

u = U_m sin ωt. (5.1)

Так как цепь обладает только активным сопротивлением, то по закону Ома для участка цепи:

i = = = I_m sin ωt, (5.2)

где – закон Ома для амплитудных значений.

Разделив левую и правую части этого выражения на , получим

– закон Ома для действующих значений,

где I = , U = .

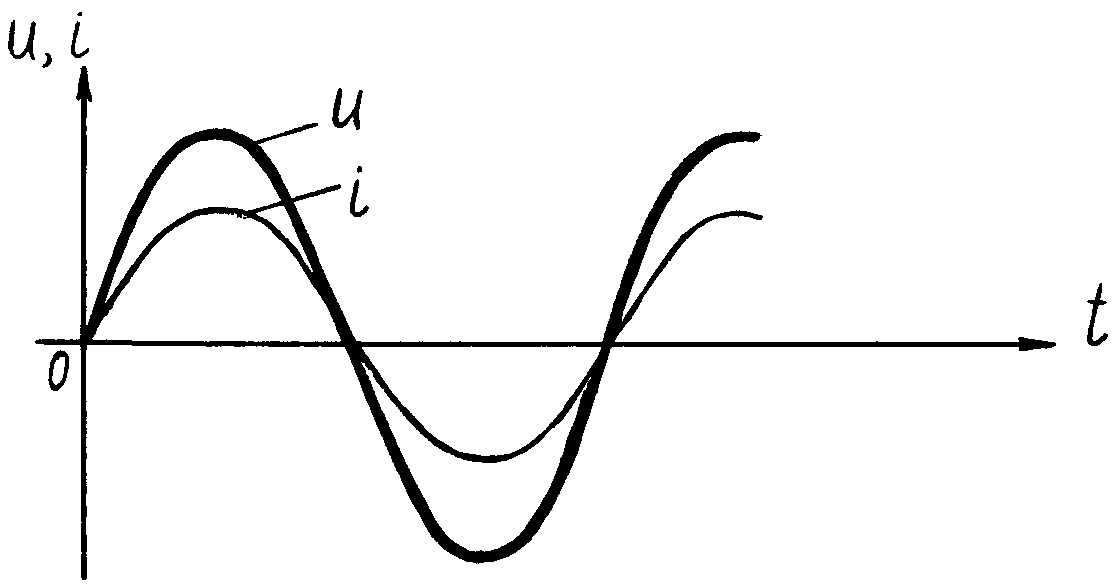
Сравнив выражения для мгновенных значений тока и напряжения (5.1) и (5.2), приходим к выводу, что ток и напряжение в цепи с активным сопротивлением совпадают по фазе.

Рис. 5.1 Временные диаграммы тока Рис. 5.2 Векторные диаграммы тока

и напряжения для цепи с активным и напряжения для цепи с активным

сопротивлением. сопротивлением.

Цепь с индуктивным сопротивлением.

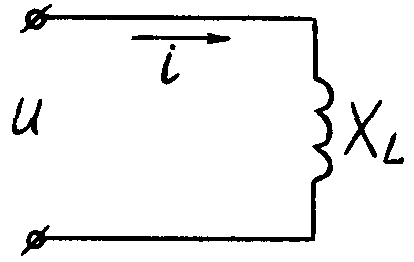
Под действием синусоидального напряжения в цепи с индуктивной катушкой протекает синусоидальный ток

i = I_m sin ωt (5.3)

В результате этого вокруг катушки возникает переменное магнитное поле и в катушке наводится ЭДС самоиндукции.

При r = 0 напряжение источника u целиком идет на уравновешивание этой ЭДС, следовательно, u = – ℮ _L.

Т. к. ℮ _L = – L , то u = L = L = L I_m ּ ω cos ωt,

где L ּ I_m ּ ω = U_m , то (5.4)

u = U_m sin (ωt + ) (5.5)

Сравним выражения для мгновенных значений тока и напряжения (5.3) и (5.5), и видим, что ток в цепи с индуктивной катушкой отстает по фазе от напряжения на угол .

Выведем закон Ома для этой цепи.

Из уравнения (5.4) следует .

Пусть L ּ ω = X_L = 2 π L f – индуктивное сопротивление цепи.

Тогда – закон Ома для амплитудных значений.

Разделив обе части этого уравнения на , получим

– закон Ома для действующих значений.

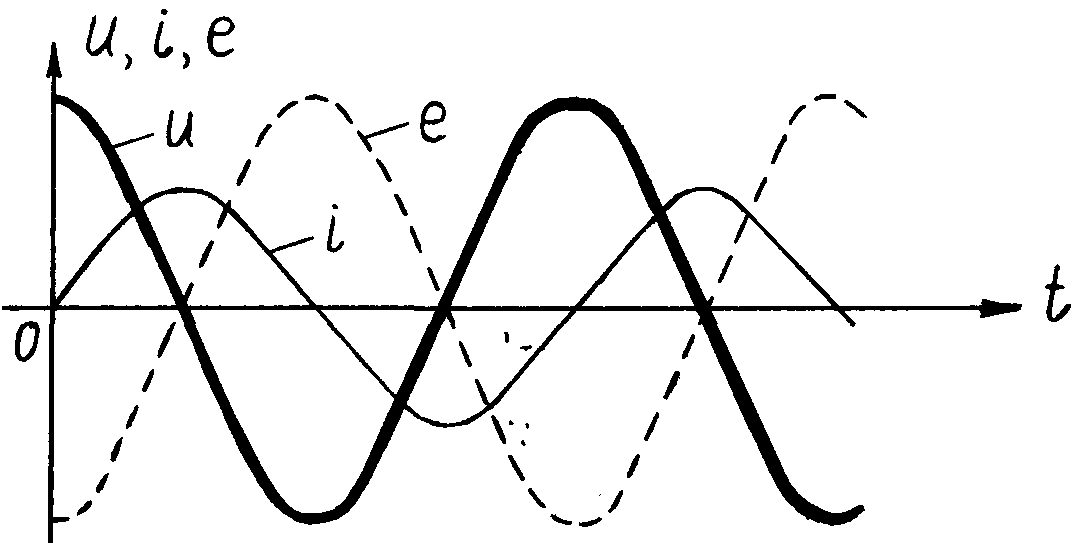
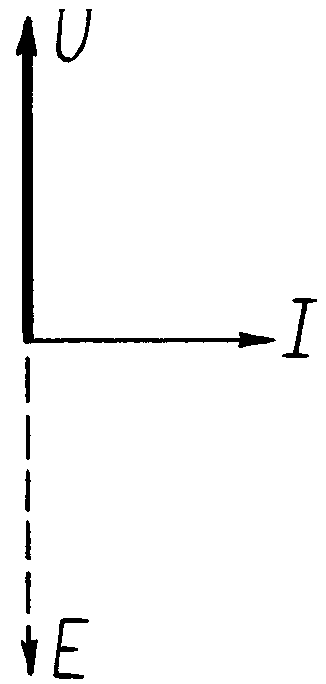
Рис. 5.3 Временные диаграммы тока, Рис. 5.4 Векторные диаграммы тока,

напряжения и ЭДС для цепи напряжения и ЭДС для цепи

с индуктивной катушкой. с индуктивной катушкой

Ц

епь с емкостным сопротивлением

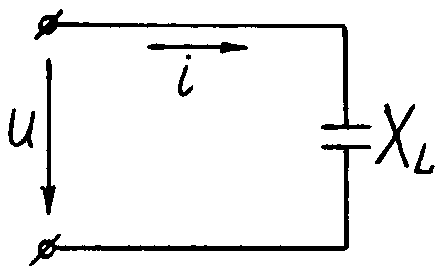
Пусть u = U_m sin ωt (5.6),

тогда ток в цепи будет меняться по синусоидальному закону.

Используя определение тока i = , если q = C ּ u.

Следовательно,

i = = U_m ω C cos ω t = U_m ω C sin (ω t + ),

где U_m ω C = I_m , тогда (5.7)

i =I_m sin (ω t + ) (5.8)

Таким образом, ток в цепи с емкостью опережает по фазе напряжение на угол .

Выведем закон Ома для этой цепи.

Представим уравнение (5.7) в виде I_m = .

Пусть – емкостное сопротивление.

Тогда I_m = – закон Ома для амплитудных значений,

I = – закон Ома для действующих значений.

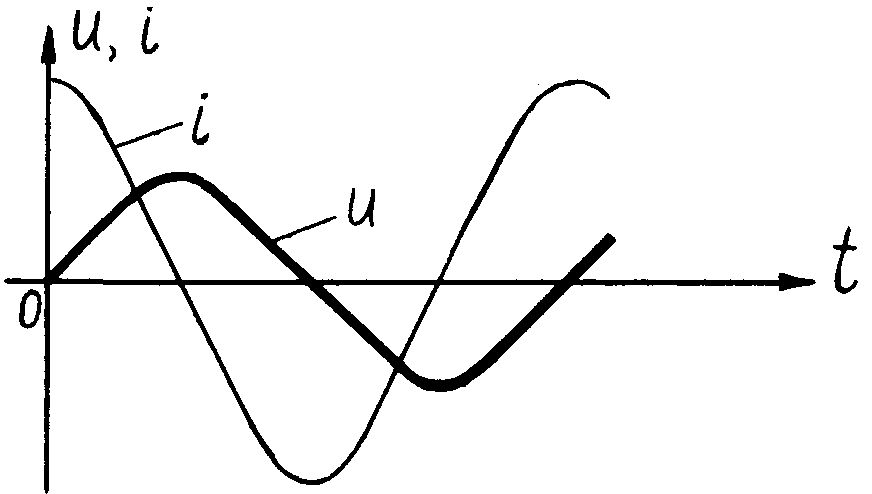
Рис. 5.5 Временные диаграммы тока и Рис. 5.6 Векторные диаграммы тока и

напряжения для цепи с емкостью напряжения для цепи с емкостью