4. Магнитные цепи

Магнитные цепи служат для формирования рабочего магнитного потока в электрических машинах, трансформаторах, электроизмерительных приборах и других электромагнитных устройствах.

Часть электромагнитного устройства, содержащую ферромагнитные тела, в которой при наличии намагничивающей силы возникает и вдоль которой замыкается магнитный поток, называют магнитной цепью.

Намагничивающую силу создают обмотки с электрическим током или постоянные магниты. Часть магнитной цепи, по которой замыкается магнитный поток, изготовляют в основном из ферромагнитных материалов и называют магнитопроводом.

Магнитные цепи бывают неразветвленными (рис. 4.10, 4.11) и разветвленными (рис. 4.12). Различают также магнитные, цепи однородные и неоднородные. Магнитопровод однородной цепи на всем его протяжении выполнен из одного материала и имеет одинаковое по форме и размерам поперечное сечение (рис. 4.10); в неоднородной цепи магнитопровод состоит из нескольких участков, отличающихся в общем случае по длине, поперечному сечению, материалам (рис. 4.11).

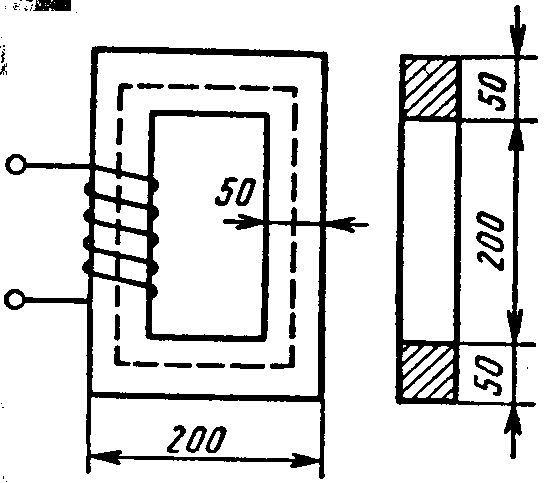
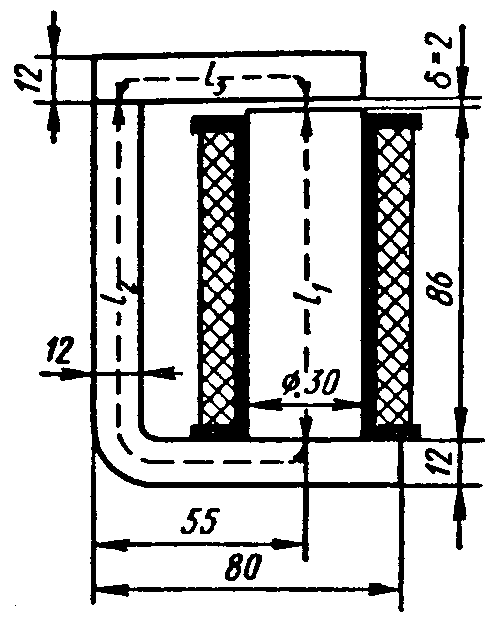
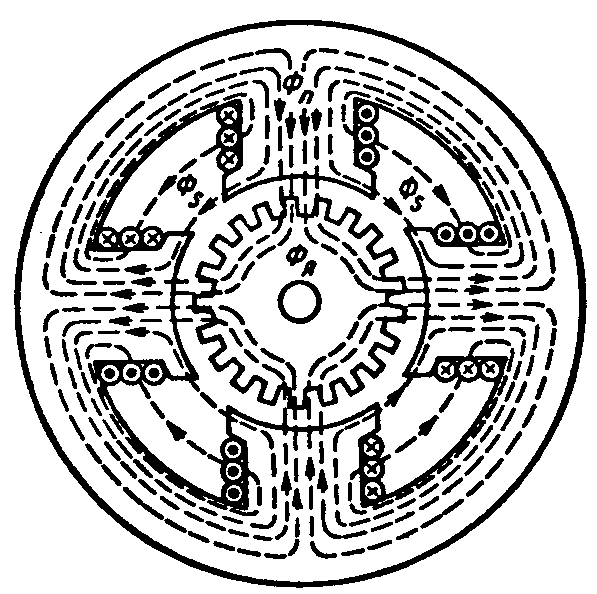
Рис. 4.10 Рис. 4.11 Рис. 4.12

Неразветвленные магнитные цепи. При расчете и конструировании магнитных цепей выбирают их формы, размеры, материалы, расположение источников намагничивающей силы (обмоток с токами, постоянных магнитов). Полагая, что конструкция магнитной цепи известна, рассмотрим прямую и обратную задачи расчета сначала в простейшем случае для однородной цепи (рис. 4.10) без учета потоков рассеяния.

В прямой задаче задан магнитный поток Ф, требуется определить намагничивающую силу, необходимую для создания этого потока.

Задачу решают следующим образом: 1) магнитная индукция В = Ф / S; 2) напряжен-ность магнитного поля Н в сердечнике определяют по кривой намагничивания В = f (H) материала сердечника (рис. 4.8); 3) намагничивающая сила IN = Hl, где l — длина магнитопровода по средней линии без учета закруглений.

Обратную задачу, в которой по заданной намагничивающей силе определяют магнитный поток, решают в обратной последовательности: 1) напряженность магнитного поля H = IN / l; 2) магнитная индукция — по кривой намагничивания; 3) магнитный поток Ф = ВS.

Для конкретных величин В и Н, найденных при решении задачи, можно подсчитать статическую магнитную проницаемость данного материала сердечника по формуле (4.19)

μ_а = В / Н. Тогда магнитная индукция B = μ_аIN / l, а магнитный поток Ф = μ_аINS / l = = IN / (l / μ_аS). Обозначив знаменатель этого выражения l / μ_аS = R_м, получим для магнитного потока

Ф = IN / R_м = F / R_м, (4.22)

где F = IN — намагничивающая сила.

Формула (4.22) похожа на выражение закона Ома для электрической цепи.

По аналогии с э.д.с. Е в электрической цепи намагничивающую силу F в магнитной цепи называют магнитодвижущей силой м.д.с., а R_м — магнитным сопротивлением.

Расчет магнитных цепей обычно проводят без определения магнитного сопротивления R_м. Это понятие используют в некоторых случаях при качественном рассмотрении явлений в магнитных цепях. Согласно формуле (4.21), намагничивающая сила для однородной магнитной цепи численно равна произведению напряженности магнитного поля и длины магнитопровода Hl. Эту величину называют магнитным напряжением и обозначают U_m (U_m = Н l).

Отмеченная ранее аналогия между магнитными и электрическими цепями распространяется и на цепи с неоднородными магнитопроводами. Доказано, что для магнитной цепи можно составить уравнение по закону полного тока, по форме аналогичное контурному уравнению, составленному для электрической цепи согласно второму закону Кирхгофа.

В левую часть такого уравнения записывают алгебраическую сумму намагничивающих сил, встречающихся при обходе данного магнитного контура (намагничивающую силу считают положительной, если ее направление совпадает с направлением обхода); в правую часть уравнения записывают алгебраическую сумму магнитных напряжений участков магнитопровода (Н_n l_n = U_mn), называют магнитным напряжением данного участка магнитной цепи, по аналогии с напряжением на участке электрической цепи, и считают его положительным, если направление магнитного потока на этом участке совпадает с направлением обхода

. (4.23)

Это уравнение применяют для решения прямой задачи расчета неоднородной магнитной цепи. Неразветвленную цепь в этом случае делят на однородные участки и для каждого из них определяют магнитную индукцию В_n, а затем находят значения напряженности магнитного поля Н_n и магнитного напряжения U_mn. По уравнению (4.23) определяют намагничивающую силу F, необходимую для получения заданного магнитного потока.

Обратную задачу — определение магнитного потока по заданным намагничивающим силам — нельзя решить так же просто, как для однородной цепи, так как неизвестно распределение магнитных напряжений между участками. Для решения обратной задачи применяют графоаналитические методы, которые здесь не рассматриваются.

Разветвленные магнитные цепи. В разветвленной магнитной цепи, по аналогии с электрической цепью, можно выделить контуры, ветви и отметить узлы. Магнитные потоки в общем случае различны в различных ветвях (рис. 4.12).

Для разветвленных магнитных цепей можно составить узловые уравнения (ΣФ = 0) и контурные уравнения (ΣФ = ΣНl). Алгебраическое решение системы узловых и контурных уравнений магнитной цепи обычными способами невозможно, так как эта система нелинейная. Поэтому в практике применяют графические и графоаналитические методы расчета разветвленных магнитных цепей.

Однако симметричную разветвленную магнитную цепь (рис. 4.12) условно можно разделить на контуры так, что во всех Участках выделенного контура магнитный поток будет один и тот жe. Кроме того, предполагается симметричное расположение обмоток с токами. Расчет симметричной магнитной цепи можно свести к расчету одного контура в том порядке, в котором рассчитывают неразветвленные цепи.