4. Электромагнетизм

1. Основные свойства и характеристики магнитного поля ………………………… 46

2. Индуктивность ……………………………………………………………………….… 49

3. Магнитные свойства веществ ……………………………………………………….. 50

4. Магнитные цепи……………………………………………………………………….. 54

5. Электромагнитные силы. Энергия магнитного поля …………………………….. 56

6. Электромагнитная индукция ………………………………………………………… 59

Основные формулы.………………………………………………………. 63

Обозначения.……………………………………………………………….. 63

Примеры решения задач.…………………………………………………. 64

Контрольные вопросы ……………………………………………………. 67

Задачи для самостоятельного решения ………………………………... 68

1. Основные свойства и характеристики магнитного поля.

Магнитное поле обнаруживается в пространстве, окружающем движущиеся заряженные частицы, с которыми это поле связано. В проводнике и пространстве вокруг него магнитное поле обусловлено этим током, а внутри и вокруг намагниченного тела — внутриатомным и внутримолекулярным движением заряженных частиц (например, вращением электронов вокруг своих осей и вокруг ядра атома).

Главным свойством магнитного поля является силовое действие на движущуюся электрически заряженную частицу, причем сила воздействия пропорциональна заряду частицы и ее скорости.

Это свойство магнитного поля положено в основу для определения его количественных характеристик, без которых невозможны изучение магнитных явлений и расчеты, связанные с их практическим использованием.

З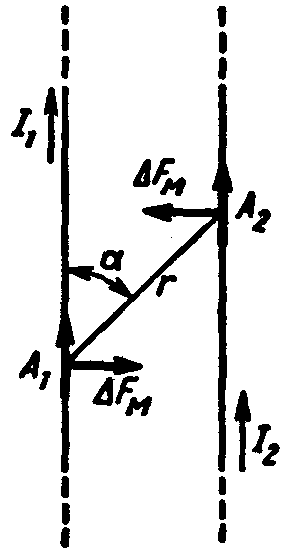 акон Ампера. В 1820 г. Ампер установил закон, выражающий силу взаимодействия электрических токов.

Величина, численно равная произведению тока проводимости (I) вдоль линейного проводника и бесконечно малого отрезка этого проводника (Δ l): А = I Δ l называется элементом тока.

Сила взаимодействия двух элементов тока прямо пропорциональна произведению этих элементов тока и обратно пропорциональна квадрату расстояния между ними:

Δ F_м = , (4.1)

г

Рис. 4.1

де Δ F_м – элементарная магнитная сила, Н;

А – элемент тока, Аּм;

r – расстояние между элементами тока;

α – угол между направлениями А₁ и r;

μ₀ = 4π ּl0^-7 (Гн/м) – магнитная постоянная.

Предположим, что источником магнитного поля является провод с током I₁, а ток I₂ настолько мал, что не изменяет характеристик этого поля. В данном случае элемент тока А₂ является пробным, с помощью которого можно обнаружить силу F_м и исследовать магнитное поле в различных точках пространства.

Каждый из двух элементов тока (A₁ и А₂) создает свое магнитное поле; в окружающем их пространстве одно поле накладывается на другое и образуется общее магнитное поле (принцип наложения полей). Силовое взаимодействие двух токов следует рассматривать как результат действия на каждый из них общего магнитного поля, созданного этими токами.

Магнитная индукция. Важные для практики свойства и характеристики магнитного поля зависят от формы проводника, значения и направления тока в нем, от взаимного расположения проводников (если поле создается группой проводников), свойств среды и т. д. Поэтому магнитные поля, созданные при различных условиях, отличаются одно от другого по форме и количественным показателям.

Для того чтобы сопоставлять магнитные поля, оценивать возможности их использования и вести соответствующие расчеты, установлены и применяются их силовые и энергетические характеристики.

Из выражения (4.1) видно, что сила F_м зависит от величины пробного элемента тока А₂, поэтому в качестве характеристик магнитного поля служить не может. Силовой характеристикой магнитного поля является вектор магнитной индукции В.

Магнитная индукция — векторная величина, численно равная отношению силы, действующей на заряженную частицу к произведению заряда и скорости частицы, если направление скорости таково, что эта сила максимальна.

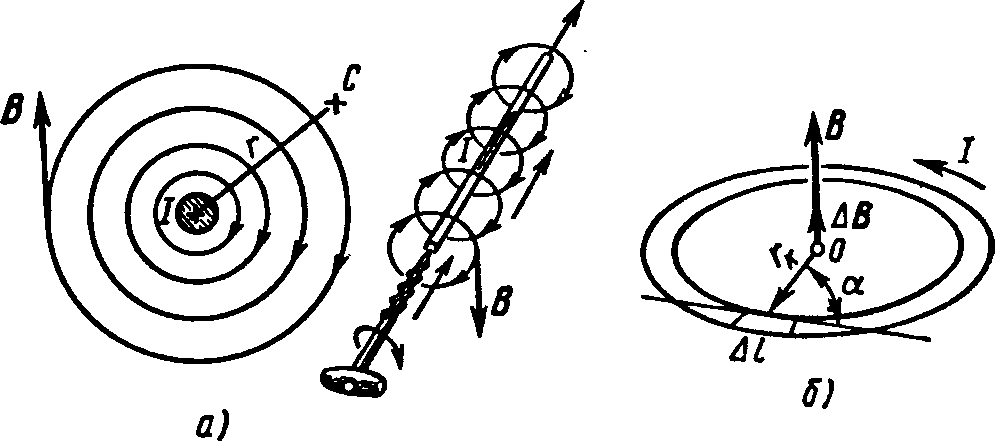
Рис. 4.2

Направление магнитной индукции перпендикулярно векторам силы и скорости v частицы.

На основе этого определения получим выражение элементарной магнитной индукции:

ΔВ = = = .

Из формулы (4.1) следует ΔВ = = ,

отсюда ΔВ = , (4.2)

где ΔВ — магнитная индукция, Тл (тесла); I Δl — пробный элемент тока, А·м.

Формула (4.2) выражает закон Био–Савара и определяет элементарную магнитную индукцию в любой точке С пространства на расстоянии r от оси провода с током.

Провод конечных размеров состоит из множества элементов, поэтому магнитную индукцию в заданной точке можно найти как векторную сумму элементарных величин ΔВ, взятую по всей длине провода.

Для длинного прямого провода с током I (рис. 4.2, а) такое решение приводит к формуле В = µ₀I/2πr, а магнитная индукция в центре кольцевого витка провода с током I (рис. 4.2, б) В = µ₀I / 2 r_к, где r_к — радиус кольцевого витка.

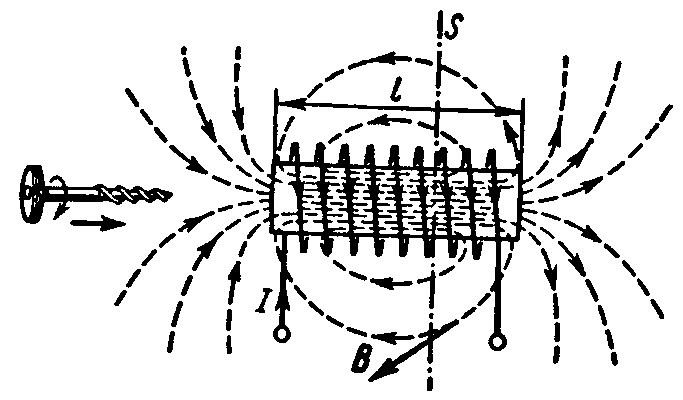
Внутри катушки (рис. 4.3, а) длиной l, имеющей N витков при токе в них I, магнитная индукция

B = µ₀I N / l. (4.3)

a) б)

Рис. 4.3

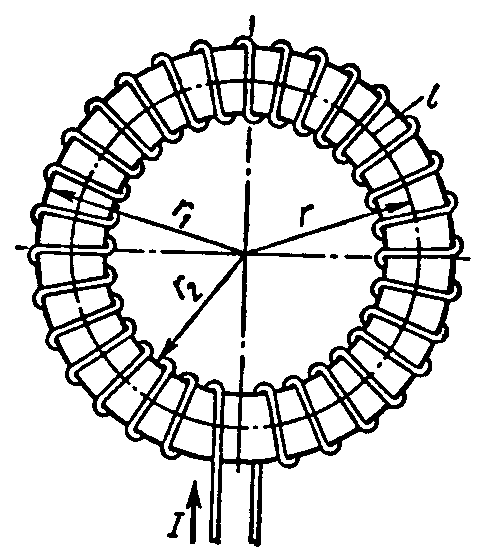
Для катушки с кольцевым неферромагнитным сердечником (рис. 4.3, б) l = 2πr, где r – радиус сердечника.

Наглядное изображение магнитного поля выполняют с помощью линий магнитной индукции (силовых линий). В каждой точке такой линии направление вектора магнитной индукции совпадает с касательной к этой линии (рис. 4.2, а, 4.3, a).

Из формулы (4.3) и рис. 4.3, а видно, что магнитная индукция внутри длинной цилиндрической катушки одинакова по величине и направлению во всех точках. Такое магнитное поле называю однородным (или равномерным).

Магнитный поток и потокосцепление. На рис. 4.3, а перпендикулярно оси катушки расположена плоскость S (след ее показан штрих-пунктирной линией). В данном случае линии магнитной индукции равномерного поля пронизывают эту плоскость под прямым углом (между направлением линий магнитной индукции и нормалью к поверхности S угол α = 0).

В качестве характеристики магнитного поля катушки, кроме величины магнитной индукции, определяют поток магнитной индукции (магнитный поток), который при заданных условий (В = const, α = 0°) выражается произведением

Ф = В S, (4.4)

где Ф — магнитный поток, Вб (вебер).

Предположим, что число линий магнитной индукции, приходящееся на единицу площади (плотность линий), численно равно величине магнитной индукции В. Тогда общее число линий внутри катушки составляет BS (S — площадь поперечного сечения катушки или площадь, ограниченная витком), т. е. численно равно потоку магнитной индукции катушки.

Если линии магнитной индукции пронизывают поверхность при α ≠ 0, то магнитный поток определяют по формуле

Ф = ВS соs α. (4.5)

Подставим в формулу (4.4) выражение магнитной индукции (4.3), получим

Ф = (4.6)

В магнитном поле катушки рис. 4.3, б рассмотрим некоторый замкнутый контур l, сцепленный с ее N витками. Полный ток, охватываемый этим контуром, выражается произведением IN. От значения полного тока прямо пропорционально зависит магнитный поток катушки [см. формулу (4.6)], поэтому величину IN называют также намагничивающей силой

F = IN, (4.7)

где F — намагничивающая сила, А.

Направление намагничивающей силы связано с направлением тока в витках катушки и его можно определить по правилу буравчика: если ручку правоходового буравчика вращать по направлению тока в витках, то поступательное движение буравчика покажет направление намагничивающей силы катушки с током (рис. 4.3, а).

Рис. 4.3, а дает наглядное представление о том, что линии магнитной индукции окружены витками катушки и замыкаются, охватывая витки. Говорят, что магнитный поток сцеплен с витками катушки, а для расчетов введена величина потокосцепления.

Сумма магнитных потоков, сцепленных с отдельными витками катушки, называется потокосцеплением.

Потокосцепление катушки, все N витков которой сцеплены с магнитным потоком Ф, выражается произведением

Ψ = ФN, (4.8)

где Ψ — потокосцепление, Вб.

Потокосцепление катушки называют собственным или потокосцеплением самоиндукции, если оно обусловлено током этой катушки. На рис. 4.4, а, б потокосцепление катушки N₁ собственное Ψ_1.1 = Ф₁N₁. Потокосцепление некоторой катушки, обусловленное электрическим током другой катушки, называют взаимным или потокосцеплением взаимной индукции.

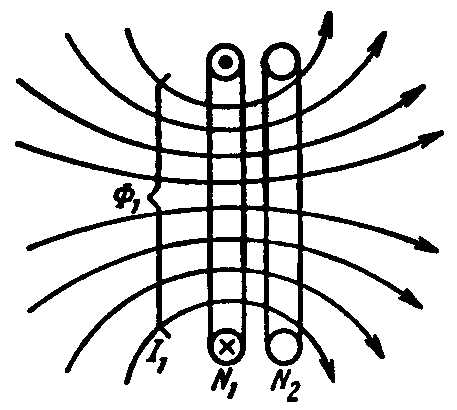
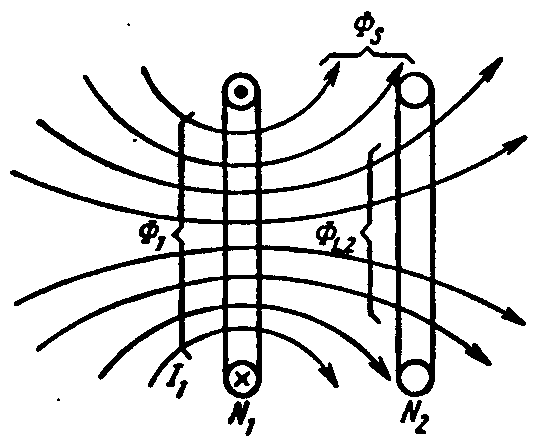
а) б)

Рис. 4.4

Катушка N₂ на рис. 4.4, а, б имеет взаимное потокосцепление Ψ_1.2 = Ф_1.2N₂, причем на рис.4.4, а Ф_1.2 = Ф₁, а на рис.4.4, б Ф_1.2 < Ф₁, так как имеется некоторый магнитный поток рассеяния Ф_s.