1.1 Характеристики математических моделей

Эффективность математической модели определяется следующими характеристиками:

1) Адекватность;

2) Степень целенаправленности поведения;

3) Сложность;

4) Целостность;

5) Поведенческая стратегия;

6) Адаптивность;

7) Управляемость;

8) Возможность развития.

Адекватность модели – соответствие математической модели объекту в отношении отображения его заданных свойств (нам выполнить эту характеристику сложно, так как нет экспериментов для определения этой характеристики);

В зависимости от степени целенаправленности модели могут быть разделены на одноцелевые и многоцелевые.

Сложность – можно оценить по общему числу элементов в системе и связей между ними.

Целенаправленность – указывает на то, что создаваемая модель является одной общей системой, включает большое количество составных частей, находящихся в сложной взаимосвязи друг с другом.

Поведенческая стратегия – дает возможность оценить эффективность достижения системы поставленной цели. Для количественной оценки эффективность управления используются критерии качества.

Адаптивность – приспосабливаемость к различным внешне -возмущенным факторам в широком диапазоне изменения воздействия внешней среды.

Управляемость модели – позволяет обеспечивать управление при экспериментах для получения возможности рассмотрения протекания процесса в различных условиях, имитирующие реальные.

Возможность развития модели – позволяет создавать мощные системы моделирования для исследования многих сторон функционирования реального объекта. Модель должна быть открытой: обеспечивать включение в ее состав новых подмоделей или подсистем управления.

Математическая модель процесса или явления представляется в следующем, общем виде:

Y (t) = φ {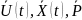 } (1.1)

где φ – вектор-функция, зависящая от управляющих воздействий, входных переменных и внутренних параметров;

Y = (Y₁, Y₂, …, Y_m) – вектор выходных переменных;

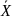= (Х₁, Х₂, …, Х_n) – вектор входных переменных;

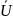= (U₁, U₂, …, U_k) – вектор управляющих воздействий;

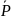= (P₁, P₂, …, P_l) – вектор внутренних параметров.

Наиболее полное отображение процессов в реальных объектах дают системы алгебраических (статистика процессов) и дифференциальных уравнений (динамика процессов), которые широко используются в математическом моделировании [1].

1.2 Модели случайных процессов

В основе методологии построения математической модели случайных процессов и зависимостей, отражающих взаимосвязи между данными, полученными экспериментальным путем, лежит теория случайных величин и регрессионный анализ.

Случайной называется величина, которая в результате одного и того же опыта может принять заранее неизвестное значение. Случайные величины могут быть: дискретными и непрерывными.

Дискретные случайные величины принимают числовые определенные значения, например – число слябов, количество приборов (могут быть перечисленными), а значение непрерывных случайных величин не могут быть заранее перечислены и непрерывно заполняют следующий промежуток, т.е. определенный промежуток, например – ошибка измерения, вес, температура, масса. Всякое соответствие между возможными значениями случайных величин и вероятностями, с которыми эти значения принимаются, называются - законом распределения случайной величины.

При решении большинства практических задач закон распределения, т.е. полная характеристика случайной величины, неудобен для использования, поэтому чаще применяют числовые характеристики случайной величины, определяющие основные показатели закона распределения. Наиболее распространенными являются математические ожидания, дисперсия и среднее квадратичное отклонение:

Математическое ожидание непрерывной случайной величины находится следующим образом:

М(Х) = 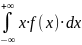(1.2)

Дисперсия D[X] (1.3) и среднее квадратическое отклонение (1.4) определяют рассеяние случайной величины около её математического ожидания и вычисляются по формулам:

D(X) = M[X – M[X]²] (1.3)

σ(X) = 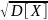(1.4)

На практике очень часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной, а двумя и более случайными величинами, образующими комплекс или систему.

Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих, они включают так же взаимные связи (зависимости) между случайными величинами – корреляциями.

Корреляция–это связь между двумя или несколькими величинами или исследуемыми объектами.

Корреляция бывает двух видов:

1) Детерминированная (определяется строгими закономерностями и обычно описывается физико-химическими формулами);

2) Стохастическая (случайная, вероятностная) – проявляется в том, что одна из величин влияет на изменение другой изменениями своего закона распределения [1].