Поляков А.С. Методическое руководство по электропрофилированию. Л., Недра. – 1969.- 200 с.

7 Электрическое профилирование (эп)

К электропрофилированию относится ряд геофизических методов основанных на применении искусственных электрических полей постоянного или переменного тока низкой частоты. Характерной особенностью методов электропрофилирования следует считать тот факт, что работы на площади изучаемого, района проводятся по линиям (профилям) для некоторой заданной глубины исследований (при постоянных размерах питающей и измерительной линий).

Промышленное применение методы электропрофилирования получили в конце 20-х годов прошлого века. В настоящее время по разнообразию решаемых задач, объемам работ и числу разновидностей они занимают ведущее место среди других методов электроразведки. Электропрофилирование широко привлекается при решении задач геологического картирования, при поисках и разведке хорошо проводящих (рудных залежей, антрацита, графита и др.) и плохо проводящих объектов (кварцевых, баритовых, пегматитовых тел и др.), карста, а также при определении мощности рыхлых образований по площади (в сочетании с ВЭЗ), при инженерно-геологических и гидрогеологических исследованиях.

7.1 Физико-математические основы методов электропрофилирования

В методах электропрофилирования изучается электрическое поле, создаваемое в земле источниками постоянного тока с помощью спе­циальных электродов (заземлителей). Электроды, с помощью которых ток вводится в землю, называются питающими или токовыми, а с по­мощью которых производится измерение электрического поля - приемными или измерительными. При электропрофилировании то­ковые и приемные электроды располагаются на дневной поверхности, на границе раздела земля - воздух.

Электрическое поле тока в любой точке проводящей среды, при отсутствии в ней объемных и поверхностных зарядов, определяется следующими уравнениями электродинамики:

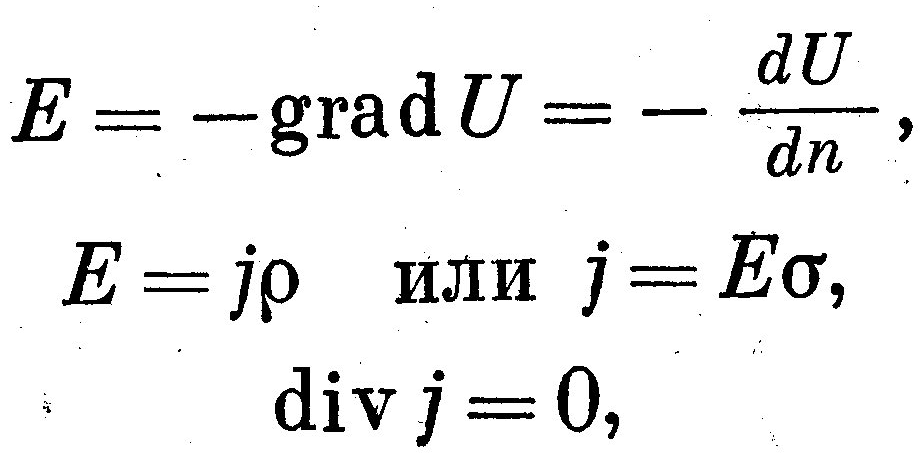
где U и Е - потенциал и напряженность электрического поля в рас­сматриваемой точке пространства; ρ и σ - удельное сопротивление и удельная электропроводность среды в данной точке; j - плотность тока в той же точке; п — направление нормали к поверхности рав­ного потенциала.

Первое уравнение выражает связь между потенциалом электри­ческого поля U и его напряженностью Е. Второе уравнение является выражением закона Ома в дифференциальной форме. Оно указы­вает, что напряженность электрического поля Е в любой точке про­странства при отсутствии в ней объемных и поверхностных зарядов пропорциональна плотности тока и удельному сопротивлению среды в данной точке. Это уравнение позволяет понять физический смысл измеряемых величин при работах в сложных геологических условиях и является основой для качественной интерпретации получаемых графиков.

Третье уравнение является первым законом Кирхгофа в дифферен­циальной форме, который выражает то факт, что алгебраическая сумма токов, вытекающих из любого объема, равна нулю если в нем нет электрических зарядов.

Для рассмотрения электрического поля в горных породах эту систему уравнений необходимо дополнить граничными условиями. Горные породы по удельному сопротивлению являются неоднородными средами. Однако для решения практических задач можно предположить, что горные породы состоят из отдельных соприкаса­ющихся участков, однородных внутри участка, но различных между собою. Электрическое поле на контакте участков характеризуется следующими граничными условиями. При отсутствии объемных и поверхностных зарядов нор­мальная составляющая плотности тока на границе двух сред непре­рывна:

где 1 и 2 — индексы сред.

Из последнего уравнения следует, что в проводящей среде на границе раздела с изолятором нормальная составляющая вектора плотности тока отсутствует, т. е. ток течет параллельно границе раздела.

Следующее условие может быть сформулировано так. При отсутствии контактных э. д. с. тангенциальные составляющие напряженности электрического поля на границе раздела двух сред не­прерывны:

где индекс l рассматривается как любое направление в плоскости, касательной к поверхности раздела. Последнее граничное условие равнозначно непрерывности потенциала на границе двух сред.

В связи с рассмотрением граничных условий необходимо отметить, что при прохождении тока через контакт двух сред на контакте могут появляться и изменяться во времени электродвижущие силы поляризации. Эти электродвижущие силы в методах электроразведки постоянного тока могут оказывать существенное влияние на измеря­емые величины.

При решении практических задач методами постоянного тока учёт границы раздела земля - воздух производится при следующих предположениях. Поверхность земли на участка растекания тока считается плоской. Источники тока располагаются непосредственно у дневной поверхности. Принимается, что над поверхностью вместо воздуха находится точно такая же среда, как и в нижнем полупро­странстве, и поверхность является плоскостью симметрии (рис. 7.1).

Рисунок 7.1 - Схема удвоения проводящей среды для учета границы раздела земля - воз­дух при решении задач электроразведки.

Распределение тока в такой неограниченной заполненной среде будет таково, что нормальная составляющая плотности тока у плоскости симметрии будет равна нулю, а распределение тока в нижнем полупространстве будет таким же, как и до заполнения средой верх­него полупространства, если силу тока, текущего в неограниченном пространстве, считать удвоенной по сравнению с силой тока, которая применяется в действительности. Таким образом, для учета гранич­ных условий задачи электроразведки решаются для неограничен­ного пространства с удвоенной силой тока. Полученное при этом решение будет действительно для нижнего полупространства.