Распределение Гаусса
Изучение случайных явлений показывает, что многие случайные величины имеют плотность распределения вероятности, выраженную формулой:
(7.14)
где
-
среднее значение случайной величины
Х,
-
среднее квадратичное отклонение.
Р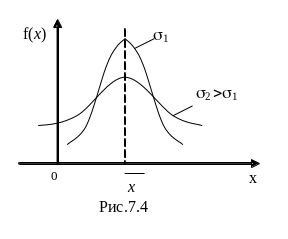
аспределение,
описываемое формулой (7.14) для множества
значений случайной величины Х, называется
распределением Гаусса или нормальным
распределением в дифференциальной
форме. Дифференциальное распределение
Гаусса при различных среднеквадратичных
отклонениях приведено на рис.7.4. Если
максимум f(x)
приходится на х=0, то распределение
называется центрированным. Для
распределения Гаусса характерно
следующее: во-первых, симметрия
относительно среднего значения случайной
величины, во-вторых, вероятность
нахождения случайной величины в интервале
от
до
равна 0,68. Это означает, что площадь
криволинейной трапеции в указанном
интервале, составляет 68% от всей площади.
Примерами распределения Гаусса являются:
распределение молекул идеального газа
по компонентам скоростей, распределение
частиц по потенциальным энергиям в поле
силы тяжести, распределение атмосферного
давления по высоте при неизменной
температуре.
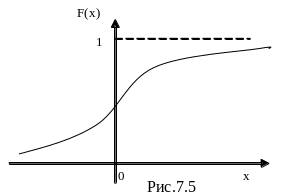
Интегральное распределение Гаусса для центрированного распределения имеет вид, представленный на рис. 7.5.
