1.4. Кінематичний розрахунок кермового приводу

Під час кінематичного розрахунку кермового приводу визначають параметричні розміри кермової трапеції, за яких забезпечується рух автомобіля на повороті без бокового ковзання коліс. Теоретично для випадку жорстких коліс бокове ковзання буде повністю відсутнім, коли при будь-яких кутах повороту керованих коліс рух автомобіля здійснюватиметься навколо єдиного центра повороту, що лежить на продовженні задньої осі.

Ця умова визначається теоретичною залежністю

(1.4.1)

де – необхідні теоретичні значення кутів повороту відповідно зовнішнього та внутрішнього по відношенню до центра повороту коліс; В – шворнева колія керованого моста; L – база автомобіля.

З достатньою для практики точністю дотримання вимоги (1.4.1) забезпечується шляхом використання кермової трапеції, схема якої показана на рис. 1.4.1.

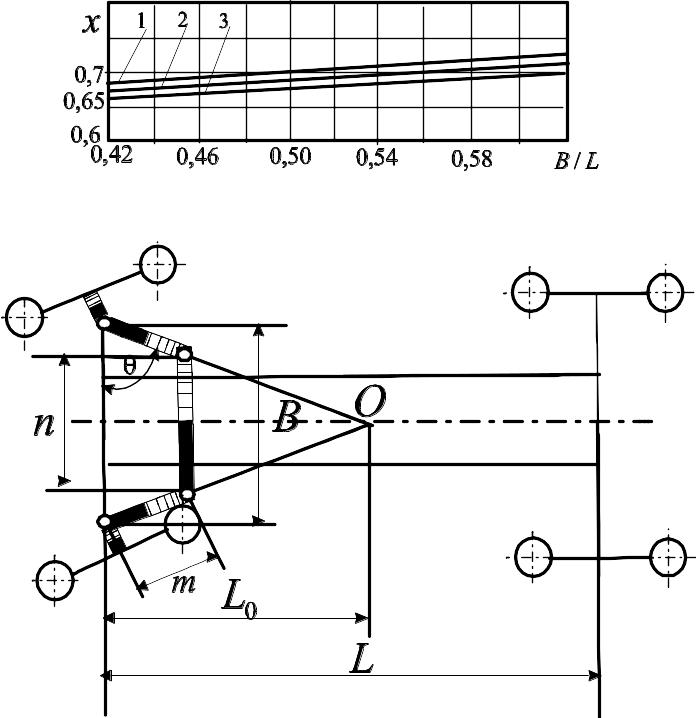
а б

Рис. 1.4.1. Схема кермової трапеції (а) і залежність х від B/L (б): 1-3 при рівному відповідно 0,12; 0,14; 0,16

Параметричними розмірами кермової трапеції є шворнева колія В, відстань n між центрами кульових шарнірів важелів трапеції, довжина m і кут нахилу важелів.

Шворнева колія В визначається компонуванням керованого моста, інші розміри, враховуючи такі міркування. В існуючих конструкціях точка О перетину осей бокових важелів трапеції віддалена на від передньої осі, якщо трапеція задня, і на якщо трапеція передня. Розміри , п і m визначають за формулами:

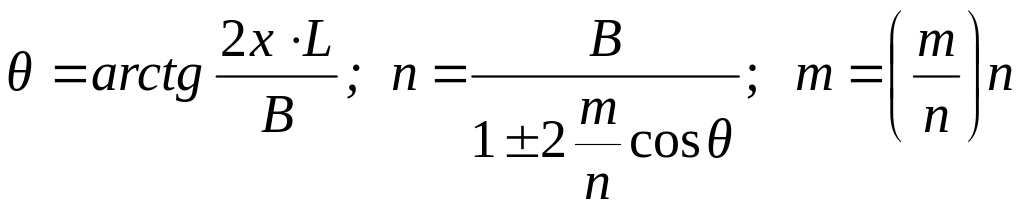(1.4.2)

де m – довжина бокового важеля кермової трапеції.

У знаменнику середньої формули знак " +" беруть при розрахунку розміру n задньої трапеції, знак "-" – передньої. Значення x визначається із графіка (рис. 1.4.1, б) для трьох значень відношення .

Формулами (1.4.2) можна користуватись, задавшись відношенням довжини m бокового важеля до довжини n поперечної тяги. Здебільшого вказане відношення лежить у межах = 0,12...0,16. Задавшись мінімум трьома значеннями відношення із вказаного діапазону, розраховують за формулами (1.4.2) розміри трьох варіантів кермової трапеції. За отриманими даними виконують у мінімально можливому масштабі графічну побудову кожної схеми кермової трапеції (чим менший масштаб, тим більша точність побудови). Потім, побудувавши через рівні кути повороту (наприклад, ) положення поворотного кулака зовнішнього колеса, графічно знаходять відповідний кут повороту поворотного кулака внутрішнього колеса.

Необхідне значення максимального кута повороту зовнішнього колеса визначається із умови забезпечення мінімального радіуса повороту автомобіля R_min, тобто радіуса середини сліду цього колеса при повороті з максимальною кривизною, за формулою

Виконавши побудову, для прийнятих схем кермової трапеції розраховують для всіх значень кутів повороту керованих коліс величину

(1.4.3)

К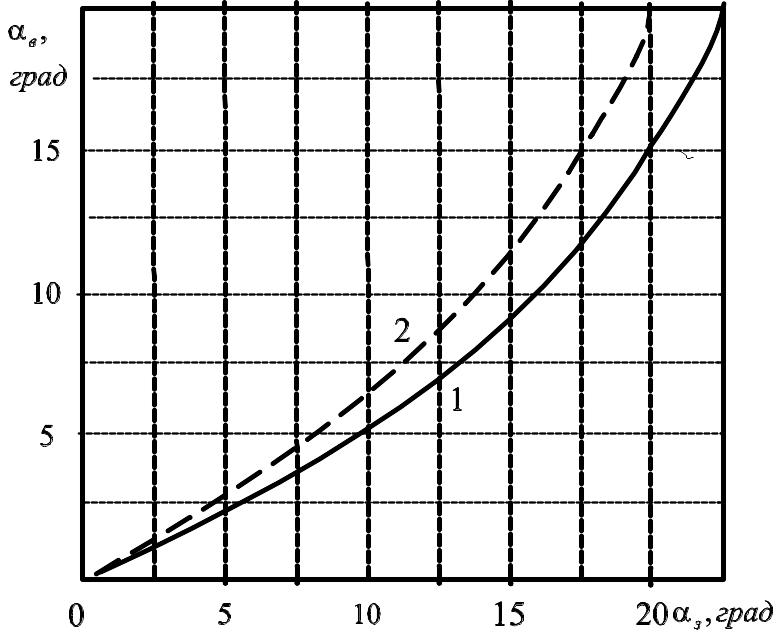 ращим буде той варіант кермової трапеції, за якого величина в найменшому ступені відхиляється від 1 при найбільш вживаних значеннях кутів повороту керованих коліс. Така кермова трапеція забезпечує співвідношення між кутами повороту внутрішнього та зовнішнього керованих коліс, за якого поворот здійснюється з найменшим боковим ковзанням. Для вибраного варіанта кермової трапеції будують графік фактичної залежності , вигляд якого зображений на рис.1.4.2. Потім за формулою (1.4.1) розраховують та будують графік теоретичної залежності .

Рис. 1.4.2. Графік залежності кутів повороту керованих коліс: 1 – фактична залежність; 2 – теоретична залежність

Якщо максимальна розбіжність між фактичним та теоретичним значеннями не перевищує при максимальному куті повороту зовнішнього колеса, то вважають, що трапеція забезпечує правильну кінематику повороту керованих коліс.

У разі невиконання цієї умови необхідно будувати та розраховувати наступний (четвертий і т.д.) варіант кермової трапеції.