3. Маркування мереж Петрі

Маркуванням є присвоєння фішок позиціям мережі Петрі. Фішка - це примітивне поняття мереж Петрі (подібно позиціям і переходам). Фішки привласнюються (можна вважати, що вони належать) позиціям. Кількість і положення фішок при виконанні мережі Петрі можуть змінюватися. Фішки використаються для визначення виконання мережі Петрі.

Визначення 5. Маркування мережі Петрі С = (Р, Т, I, О) є функція, що відображає множину позицій Р у множині ненегативних цілих чисел N.

: Р N.

Маркування може бути також визначена як n-вектор = = ( ₁, ₂, ...., _n). де п= і кожне N, i = 1, ..., п.

Рис. 11. Маркірована мережа Петрі. Структура мережі Петрі збігається зі структурами на рис. 1 і 4. Маркування - (1, 2, 0, 0, 1)

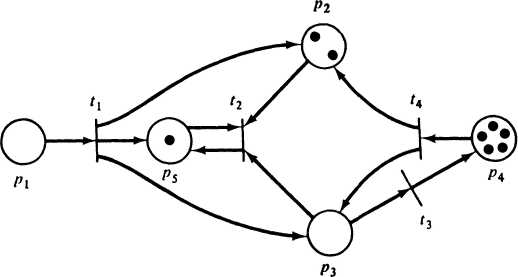
Рис. 12. Маркірована мережа Петрі. Структура аналогічна структурі, зображеної на рис. 11, але маркування відрізняється

Вектор визначає для кожної позиції p_i мережі Петрі кількість фішок у цій позиції. Кількість фішок у позиції р_i є _i, i = 1, ..., n. Зв'язок між визначеннями маркування як функції і як вектора очевидним образом установлюється співвідношенням (p_i)= _i. Позначення її у вигляді функції є трохи більше загальним і тому вживається набагато частіше.

Маркірована мережа Петрі М = (З, ) є сукупність структури мережі Петрі З = (Р, Т, I, О) і маркування і може бути записана у вигляді М = (Р, Т, I, О, ).

На графі мережі Петрі фішки зображуються маленькою крапкою в кружку, що представляє позицію мережі Петрі. На рис. 11 і 12 наведені приклади графічного подання маркірованої мережі Петрі.

Тому що кількість фішок, що може бути визначене для кожної позиції, необмежено, те в цілому для мережі Петрі існує нескінченно багато маркувань. Множина всіх маркувань мережі Петрі, що володіє n позиціями, є множина всіх n-векторів, Nⁿ. Це множина, хоча і нескінченно, є рахунковим.

Рис. 13. Граф мережі Петрі з дуже великим маркуванням (47, 13, 7, 42)

Вправи

1. Для маркірованої мережі Петрі (рис. 12) представте маркування як функцію і як вектор.

2. Для структури мережі Петрі (рис. 2) зобразите граф мережі Петрі і укажіть на графі маркування = (1, 0, 1, 1, 0, 0).

3. Кількість фішок у мережі Петрі рідко перевищує 5 або 6. У цьому випадку їх малюють. Однак, коли маркування має 10, 20 або сотні фішок, приписаних позиції, у кружках зручніше не малювати фішки, а вказувати їхня загальна кількість, як на рис. 2.13. Використовуючи цей спосіб, зобразіть маркування = (137, 22, 2, 0, 14) для мережі Петрі на рис. 12.

4. Правила виконання мереж Петрі

Виконанням мережі Петрі управляють кількість і розподіл фішок у мережі. Фішки перебувають у кружках і управляють виконанням переходів мережі. Мережа Петрі виконується за допомогою запусків переходів. Перехід запускається видаленням фішок з його вхідних позицій і утворенням нових фішок, що поміщають у його вихідні позиції.

Перехід може запускатися тільки в тому випадку, коли він дозволений. Перехід називається дозволеним, якщо кожна з його вхідних позицій має число фішок принаймні рівне числу дуг з позиції в перехід. Кратні фішки необхідні для кратних вхідних дуг. Фішки у вхідній позиції, які дозволяють перехід, називаються його розв'язними фішками. Наприклад, якщо позиції p₁ і р₂ служать входами для переходу t₄, тоді t₄ дозволений, якщо p₁ і р₂ мають хоча б по одній фішці. Для переходу t₇ із вхідним комплектом {р₆, р₆, р₆} позиція р₆ повинна володіти принаймні трьома фішками, для того щоб t₇ був дозволений.

Визначення 6. Перехід t_j Т у маркірованої мережі Петрі С = {Р, Т, I, О) з маркуванням , дозволений, якщо для всіх p_i P

(p_i) #(p_i, I(t_j)).

Перехід запускається видаленням всіх розв'язних фішок з його вхідних позицій і наступним приміщенням у кожну з його вихідних позицій по одній фішці для кожної дуги. Кратні фішки створюються для кратних вихідних дуг. Перехід t₃ з I(t₃) = {р₂} і O(t₃) = {р₇, р₁₃} дозволений щораз, коли в р₂ буде хоча б одна фішка. Перехід t₃ запускається видаленням однієї фішки з позиції р₂ і приміщенням однієї фішки в позицію р₇ і в p₁₃ (його виходи). Додаткові фішки в позиції р₂ не впливають на запуск t₃ (хоча вони можуть дозволяти додаткові запуски t₃). Перехід t₂, у якому I(t₂) = {p₂₁, р₂₃} і O(t₂) = {р₂₃, р₂₅, р₂₅}, запускається видаленням однієї фішки з p₂₁ і однієї фішки з р₂₃, при цьому одна фішка міститься в р₂₃ і дві в — р₂₅ (тому що р₂₅ має кратність, рівну двом).

Запуск переходу в цілому заміняє маркування мережі Петрі на нове маркування '. Помітимо також, що тому що можна запустити тільки дозволений перехід, то при запуску переходу кількість фішок у кожній позиції завжди залишається ненегативним. Запуск переходу ніколи не видалить фішку, відсутню у вхідній позиції. Якщо яка-небудь вхідна позиція переходу не має достатню кількість фішок, то перехід не дозволений і не може бути запущений.

Визначення 7. Перехід t_j у маркірованій мережі Петрі з маркуванням може бути запущений щораз, коли він дозволений. У результаті запуску дозволеного переходу t_j утвориться нове маркування ', обумовлена наступним співвідношенням: '(p_i) = (p_i) - #(p_i, I(t_j)) + #(p_i, O(t_j)).

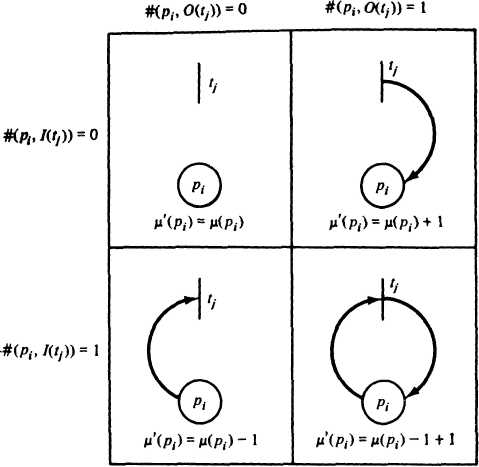
Рис. 14. Ілюстрація того, як міняється маркування позицій, коли запущений перехід t_j. Кожна позиція може або не може бути входом або виходом переходу. Тут показаний випадок для кратності 0 або 1.

Запуски можуть здійснюватися доти, поки існує хоча б один дозволений перехід. Коли не залишиться жодного дозволеного переходу, виконання припиняється.

Вправи

1. Які переходи дозволені в маркірованій мережі Петрі на рис. 11, 12?

2. Яке маркування вийде при запуску переходу t₁ (рис. 11)? Яке маркування вийде при запуску переходу t₄ (рис. 12)? Яке маркування вийде в результаті виконання наступних операцій: спочатку — запуск t₄, потім — запуск t₂ (рис. 12)?

3. Які переходи дозволені в мережі Петрі на рис. 13? Які маркування утворяться при запуску кожного із цих переходів?