2.4. Основные параметры переводной кривой

Радиус переводной кривой соответствует радиусу в корне остряка, т.е.

м

Длина прямой вставки перед крестовиной определяется по формуле:

м

2.5. Основные разбивочные размеры сп

К разбивочным размерам стрелочного перевода относятся (рис. 2.5):

– теоретическая длина СП, т.е. расстояние от начала остряка до математического центра крестовины, м

– полная длина стрелочного перевода, м

– расстояние от центра Ц до начала рамного рельса, м

– расстояние между началом остряка и центром Ц, м

– расстояние от центра Ц до конца крестовины, м

– расстояние между центром Ц и математическим центром крестовины, м

– расстояние между центром Ц и предельным столбиком, м

– расстояние от математического центра до предельного столбика, м

Теоретическая длина стрелочного перевода определяется проекцией расчетного контура ABCD на горизонталь:

, где g=2.05 м – расстояние от оси прямого направления до предельного столбика.

2.6. Расчет длины остряков и тяговых усилий для их перевода

Определение геометрических параметров гибких остряков и тяговых усилий для их перевода сводится к выбору целесообразной длины остряков при выполнении ряда ограничивающих условий. В качестве ограничений, налагаемых на результаты расчета, приняты:

• величина желоба t между рамным рельсом и отведенным остряком; на всем протяжении остряка величина t должна быть не менее минимально допустимого значения hmin= 6,7 см.

• длина остряка не должна быть более длины нормального рельса (25 м).

• напряжение σ от изгиба остряка, находящегося в отведенном состоянии, не должно быть в самом опасном сечении (в заделке) более допустимого значения [σ].

• расчетное усилие на приводе Р не должно превышать допустимой величины [Ркр] для принятого в проекте электропривода.

С математической точки зрения задачу определения длины остряков и тяговых усилий можно представить как задачу на отыскание условного экстремума, в которой в качестве целевой функции как раз и выступает длина остряка. При этом переменными, от которых зависит длина, являются:

• изгибная жесткость остряка EI;

• сила трения подошвы острякового рельса по стрелочным подушкам

, где

р – погонная масса острякового рельса;

μ – коэффициент трения;

• расположение первой тяги Lo относительно принятого начала координат;

• расположение второй тяги L1 относительно принятого начала координат при числе тяг, равное 2;

• величина желоба Ш (шаг остряка) – расстояние в свету на расчетном уровне между рамным рельсом и отведенным остряком, измеренное против первой тяги.

При построении расчетного алгоритма принимается, что остряк представляет собой консольную балку, заделанную в корневой части, на балку действуют усилия в переводных тягах, а также по всей длине равномерно распределенная нагрузка, отражающая влияние сил трения q по стрелочным подушкам. Расчетная схема приведена на рис. 2.6.1:

Рис.2.6.1. Расчетная схема определения деформаций гибкого остряка

Для расчета остряков используем программу.

Принимаем:

Ш = 15,2 см – ход остряка против первой тяги;

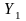= 7,2 см – ход остряка против первой тяги;

= 0,2 – коэффициент трения остряка по подушкам.

Полную длину остряка получим:

, где

а = 400 мм – расстояние от острия остряка до оси первой тяги;

b – длина корневой заделки, может быть найдена по формуле:

bi = 0,5 м – расстояние между брусьями;

ni– количество брусьев. При N >18 принимается n=5.

Результат расчета представлен на рисунке 2.6.2.

Рис. 2.6.2

Окончательно получим полную длину остряка: