1. Особливості розрахунку кіл змінного струму

Змінними називаються ЕРС, напруги і струми, які періодично змінюються в часі.

В сучасному електроустаткуванні найбільше застосування отримали змінні струми, величина (і напрямок) яких змінюються за синусоїдальним законом – синусоїдальні струми.

Значення змінних величин (ЕРС, напруг, струмів, потужностей) в будь-який момент часу називаються миттєвими і позначаються буквами е, u, i, p.

Для синусоїдальних струмів миттєве значення визначається виразом i = I_m sin(t + ), де I_m – найбільше миттєве значення періодично змінюваних величин, що називається амплітудним значенням. Аналогічно визначаються і напруги та ЕРС.

Час Т, за який струм (напруга, ЕРС) здійснює повний цикл своїх змін називають періодом змінного струму (напруги, ЕРС), а число періодів за секунду – його циклічною частотою f = 1/T. Одиниця частоти – Гц. Частота дорівнює 1 Гц, якщо повний цикл зміни струму здійснюється за 1 секунду.

Синусоїдальний характер змінного струму зумовлений характером змінної ЕРС, що утворюється в статорі генератора. Ротор обертається з кутовою швидкістю  =  / t. Якщо покласти  = 2 (повний оберт), а це буде за час t = Т, за який струм здійснить повний цикл своїх змін, то  = 2 / Т = 2 f. Ця величина () називається круговою частотою.

В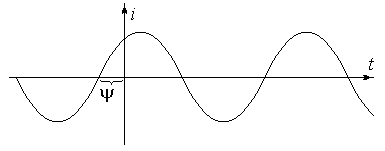 ід спостерігача залежить з якого моменту почати спостереження за зміною струму. Тому у виразі i = I_m sin(t + ) присутня величина , що називається початковою фазою, і яка визначає відставання моменту початку спостереження від початку поточного періоду⁵. Якщо  = 0, то i = I_m sin t.

Між двома синусоїдальними величинами, що мають різні ₁ і ₂, існує зсув фаз  = ₂ – ₁. Ця величина більш цікава, оскільки при дослідженні двох синусоїдальних величин завжди початкову фазу однієї можна взяти нульовою, тоді початкова фаза іншої становитиме  і вже не залежатиме від суб’єктивного вибору початку спостереження.

Діюче значення змінного струму дорівнює значенню еквівалентного постійного струму, який утворює на незмінному опорі стільки ж теплоти, як і змінний струм.

Діюче значення змінного синусоїдального струму менше його амплітудного значення в раз. Таке ж співвідношення між діючими і амплітудними значеннями для напруг і ЕРС. Діючі значення позначаються I, U, E.

Отже для аналізу синусоїдального струму необхідно знати: амплітудне (І_m, U_m, E_m) або діюче (І, U, E) значення; частоту коливань (, f або Т :  = 2f, f = 1/T) і початкову фазу .

Для розрахунків кіл змінного струму використовується зображення синусоїдальних величин за допомогою векторів, що обертаються.

Нехай маємо струм i = I_m sin(t +).

Для того, щоб зобразити його вектором, що обертається візьмемо прямокутну систему координат хОу. Із початку координат О під кутом  проведемо вектор , довжина якого в масштабі відповідає I_m . Якщо вектор обертати проти годинникової стрілки з кутовою швидкістю  = 2f, то його проекція на вісь ординат Оу буде змінюватись за синусоїдальним законом , тобто відображати миттєве значення струму і.

Сукупність векторів, що зображують на одному кресленні кілька синусоїдальних величин однієї частоти має назву векторна діаграма.

Вектори, що зображені на такій діаграмі мають однакову кутову частоту . Тому при обертанні їх взаємне розміщення не змінюється. Отже при побудові векторних діаграм один вектор можна направити довільно (наприклад, вздовж Ох), а інші розташовувати по відношенню до першого під різними кутами, що дорівнюють відповідним кутам зсуву фаз, і осі координат не креслити.

В більшості випадків векторні діаграми кіл змінного струму призначені для визначення співвідношень між діючими значеннями напруг і струмів. Тому діаграми звичайно будують не для амплітудних значень, а для діючих, що зумовлює лише зменшення довжини векторів в разів.

Таким чином вже можна передбачити, що при розрахунках кіл змінного струму треба буде використовувати складні перетворення з величинами, до яких входять тригонометричні функції, або виконувати графічні дії над векторами.

Ефективним методом розрахунку кіл змінного струму є символічний метод, оснований на зображенні електричних величин (струм, напруга, ЕРС, опори, провідності, потужності) комплексними числами. В цьому випадку для розрахунку кіл змінного струму можна використовувати закони Кірхгофа і всі методи розрахунку складних кіл постійного струму.

Форми запису комплексних чисел:

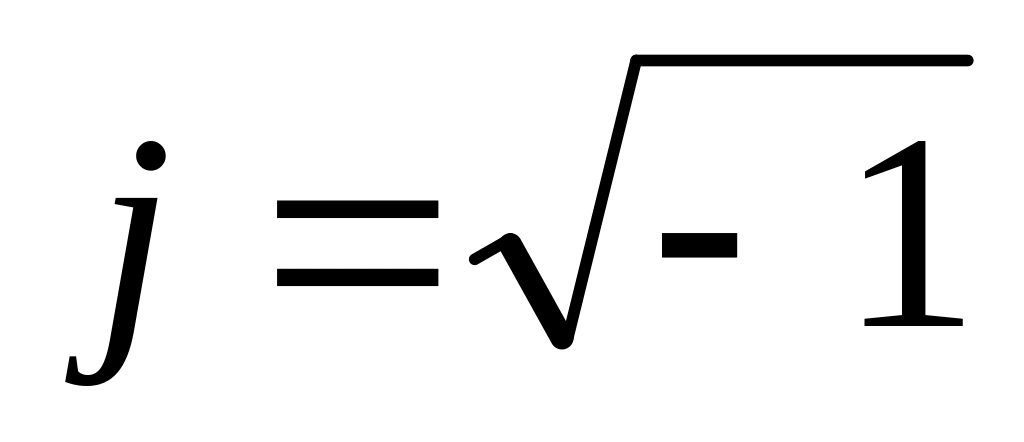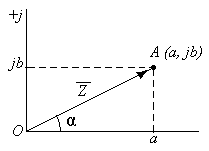
• В алгебраїчній формі комплексне число Z є сума дійсного числа a і уявного числа jb, тобто Z = a + jb. Уявне число jb є добуток уявної одиниці і коефіцієнта при ній b.

• Для зображення комплексного числа в графічній формі в прямокутній системі координат по горизонтальній осі відкладаються дійсні частини комплексного числа а, а по вертикальній осі – уявні частини jb. Комплексне число на такій комплексній площині зображується:

• точкою з координатами А(a; jb);

• вектором ОА, що починається в початку координат О, а закінчується в точці А з координатами (a; jb).

• Щоб записати комплексне число в показовій формі треба знати його модуль і аргумент. Модуль є довжина вектора ОА на комплексній площині: . Аргумент – це кут  між додатним напрямком дійсної осі і вектором ОА. Ясно, що b/a = tg , звідки  = arctg b/a.

а	b	чверть	 =
+	+	І	arctg b/a
–	+	ІІ	180 – arctg b/a
–	–	ІІІ	180 + arctg b/a
+	–	IV	– arctg b/a

При визначенні  треба мати на увазі, що обчислювальні засоби дають значення arctg b/a в межах 0   90. Тому отримане значення треба відкоригувати згідно таблиці:

Комплексне число в показовій формі є добуток модуля і множника е ^j, тобто Z = |Z| е ^j.

• Тригонометрична форма. При розрахунках із використанням комплексних чисел виникає потреба перейти від показової форми до алгебраїчної. Вихідними є модуль і аргумент. Необхідно визначити дійсну та уявну частини і представити число в алгебраїчній формі.

З трикутника a = |Z|cos , b =|Z|sin .

В комплексній формі Z = a + jb = |Z|cos  + j|Z|sin 

Отриманий запис є тригонометричною формою комплексного числа.

Для додавання або віднімання двох комплексних величин зручніше використовувати алгебраїчну форму:

Z₁  Z₂ = a₁ + jb₁  a₂ + jb₂ = (a₁  a₂) + j(b₁  b₂).

Для множення і ділення – зручніше використовувати показову форму:

Z₁  Z₂ = |Z₁| e ^j  |Z₂| e ^j = |Z₁||Z₂| e ^{j( + )};

Z₁ / Z₂ = |Z₁| e ^j / |Z₂| e ^j = |Z₁| / |Z₂| e ^{j( – )} ,

але можна і алгебраїчну:

Z₁  Z₂ = (a₁ a₂ – b₁ b₂) + j(a₁ b₂ + b₁ a₂); .

Два комплексних числа називаються спряженими, якщо відрізняються тільки знаками уявної частини (в алгебраїчній формі), або знаками аргументів (в показовій формі), наприклад:

a + jb та a – jb;

|Z| e ^j та |Z| e ^–j .

Повертаючись до електричних величин можна провести аналогію між векторами, що обертаються і комплексними векторами, якщо перші будувати на комплексній площині. Ця аналогія дозволяє синусоїдальні величини відображувати комплексними числами. Комплексні значення струмів, напруг і ЕРС прийнято позначати .

П обудуємо для кіл з активним опором, індуктивністю і ємкістю векторні діаграми, але вже на комплексній площині, вважаючи, що розташування вектора величини з нульовою початковою фазою співпадає з дійсною додатною піввіссю.

В усіх випадках вектор напруги направлений по осі дійсних чисел. Тому комплекс напруги , де U – модуль комплексу напруги, а 0 – його початкова фаза. Комплекс струму:

у першому випадку –

у другому випадку –

у третьому випадку –

Отже комплексне зображення синусоїдальних величин визначає її діюче (або амплітудне) значення і зсув фаз відносно вихідної величини, початкова фаза якої вважається рівною нулю.

При розрахунку кіл синусоїдального змінного струму використовуються закони Кірхгофа, що справедливі для миттєвих, амплітудних та діючих значень:

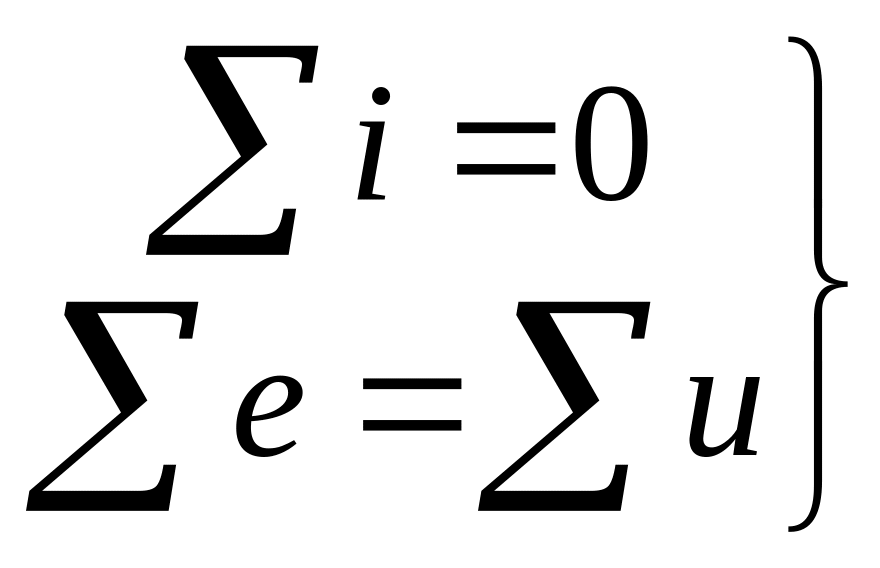для миттєвих значень – суми алгебраїчні.

Ці рівняння справедливі у векторній формі, тобто суми не алгебраїчні, а геометричні.

Суми алгебраїчні завдяки зображенню електричних величин комплексними числами.

Р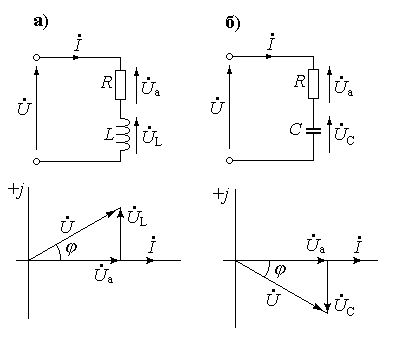 озглянемо кола:

В обох випадках вектор струму направлений по осі дійсних чисел. Комплекс напруги на клемах кола :

для випадку а) , де U_a і jU_L – дійсна і уявна частини; U і  — модуль і початкова фаза комплексу напруги.

для випадку б) .

В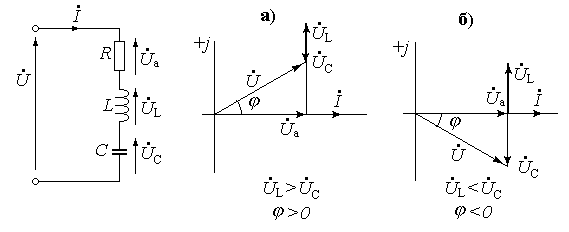 загальному виразі комплексу напруги “+” перед уявною частиною свідчить, що навантаження має індуктивний характер, “–“ — характер навантаження ємнісний.

Розглянемо електричне коло, що складається з трьох елементів:

, де

, а аргумент .

 > 0, якщо U_L > U_C

 < 0, якщо U_L < U_C.

Розрізняють повний опір Z, реактивний опір X і активний опір R, а також відповідні їм провідності: повна провідність – y = 1/Z, реактивна провідність – b = X / Z ² і активна провідність – g = R / Z ².

З розглянутих трикутників напруг (наприклад, а) і б)) = .

Це відношення є законом Ома. – повний опір кола і позначається Z. . Тобто I = U / Z .

А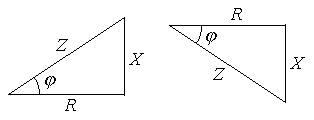 ктивний, реактивний і повний опір пов’язані між собою як сторони трикутника.

Ці трикутники також можна побудувати на комплексній площині і тоді опори виражатимуться комплексними числами:

= R + jX = R + j(X_L – X_C),

де .

Аналогічно визначаються провідності: .

При записі повної провідності в показовій формі:

модуль комплексу опору – ; аргумент – .

Я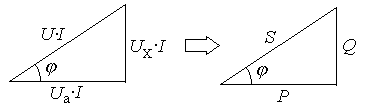 кщо сторони трикутника напруг помножити на струм І, то отримаємо трикутник потужностей:

Активна потужність – P = U_aI = UI cos  [вт];

Реактивна потужність – Q = U_ХI = UI sіn  [вар];

Повна потужність – S = UI [ва].

Формули законів Ома і Кірхгофа для кіл змінного струму в комплексній формі мають таку ж структуру, як і для кіл постійного струму. Тому методи розрахунку лінійних кіл постійного струму, що були вже розглянуті (метод безпосереднього використання законів Кірхгофа, метод суперпозиції, метод контурних струмів, метод вузлових потенціалів, метод еквівалентного генератора), можна застосовувати для розрахунку складних лінійних кіл синусоїдального змінного струму. В цьому випадку всі ЕРС, напруги, струми, опори і провідності ділянок кола визначаються так же , як і в колах постійного струму, але в комплексній формі.

2. Аналіз електричного стану трифазного кола.

ЕРС, що утворюються в трьохфазному генераторі будуть однакові за амплітудним значенням і частоті, але зсунуті за фазою відносно одна одної на 1/3 періоду. Виводи початків обмоток трифазного генератора прийнято позначати буквами А, В, С. Маркіровка виводів виконується з таким розрахунком, щоб індуковані в обмотках ЕРС E_A, E_B, E_C відставали на третину періоду E_B від E_A, E_C від E_B.

Б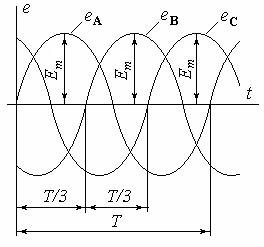 еручи за початок відліку момент часу, коли ЕРС е_А в обмотці А дорівнює нулю і змінює свої значення з від’ємних на додатні, можна записати такі вирази:

е_А = Е_m sin  t;

е_B = Е_m sin ( t – 120);

е_C = Е_m sin ( t – 240) = Е_m sin ( t + 120).

Графіки цих ЕРС мають вид:

При символічній формі запису, якщо ЕРС фази А дорівнює , то ЕРС фаз В і С відповідно складають:

В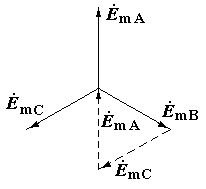 екторна діаграма для амплітудних значень ЕРС буде уявляти собою симетричну трипроменеву зірку. Для такої системи справедливе співвідношення . Таке ж співвідношення справедливе і для діючих значень .

Дійсно, з діаграми видно, що геометрична сума трьох векторів, рівних за величиною і зсунутих за фазою на третину періоду (120) дорівнює нулю. Сума миттєвих значень ЕРС трифазного генератора в будь–який момент часу також дорівнює нулю е_А + е_В + е_С = 0.

Якщо об’єднати кінці обмоток генератора в спільну точку О, а кінцеві зажими навантажень в спільну точку О, то для з’єднання генератора і трьох навантажень потрібно буде чотири проводи.

Точки О, О’ називають відповідно нульовою (або нейтральною) точкою генератора і нульовою (нейтральною) точкою навантаження.

Проводи А–А, В–В, С–С називають лінійними, а провод О–О’ – нульовим або нейтральним. Отримана схема має назву чотирипроводна система трифазного струму, або з’єднання зіркою з нульовим проводом.

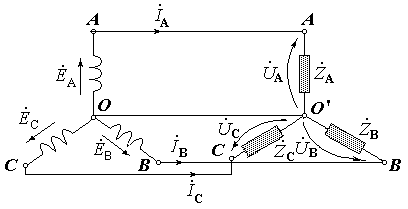
Н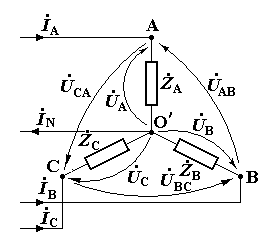 апруга між лінійним проводом і нульовим має назву фазна напруга і позначається U_A, U_B, U_C.

Напруга між лінійними проводами називається лінійною напругою і позначається U_AВ, U_BС, U_СА.

До навантажень Z_A, Z_B, Z_C прикладені фазні напруги.

В трифазних колах розрізняють лінійні І_л і фазні І_Ф струми.

Лінійними називають струми І_А, І_В, І_С, що протікають по лінійних проводах.

Струми, що протікають по обмотках генератора, або по опорах навантаження називають фазними.

При з’єднанні зіркою лінійний струм рівний фазному І_л = І_Ф.

Струм, що протікає по нульовому проводі, позначають І_N.

Для чотирипроводної системи:

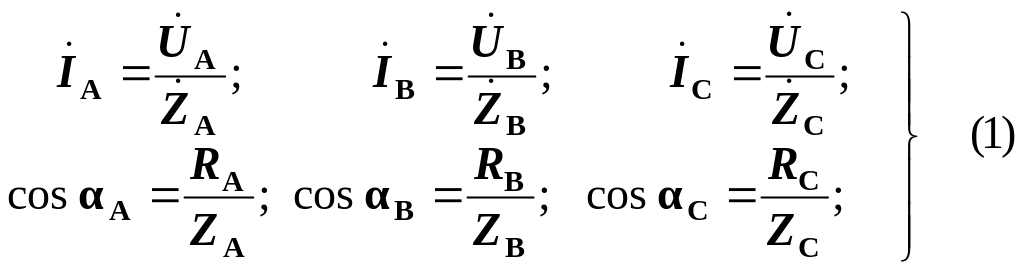
Застосувавши до нульової точки О’ перший закон Кірхгофа і прийнявши позначені на схемі додатні напрямки струмів отримаємо:

або

тобто струм в нульовому проводі визначається сумуванням лінійних струмів в комплексній формі, або геометричним сумуванням векторів І_А, І_В, І_С.

На малюнку стрілками показані додатні напрямки фазних напруг на опорах навантаження. Миттєва напруга, наприклад напруга u_AB, між лінійними проводами А і В дорівнює алгебраїчній сумі миттєвих напруг на дільниці кола між точками А і В: u_AB = u_A + (–u_B)

В цьому виразі напругу u_B взято із знаком “–“ оскільки напрям дії цієї напруги протилежний прийнятому напряму обходу кола від точки А до точки В.

Теж саме в діючих значеннях:

.

Аналогічно для лінійних напруг: і :

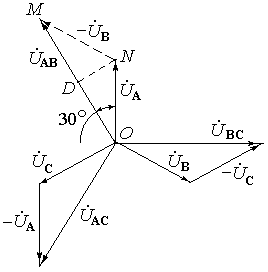В екторна діаграма напруг буде мати вид:

З діаграми видно, що всі три лінійні напруги рівні між собою за величиною і зсунуті по фазі відносно одна одної на 120.

З трикутника OMN маємо:

OM = 2OD = 2ONcos 30 = ON.

Оскільки ОМ = U_AB = U_л; ON = U_A = U_Ф, то U_л =  U_Ф, тобто лінійна напруга при з’єднанні зіркою в разів більша за фазну.

В трифазних установках навантаження окремих фаз прагнуть зробити більш-менш однаковим. При цьому струм в нульовому проводі виявляється меншим кожного з лінійних струмів. Виходячи з цього перетин нульового проводу приймають рівним приблизно половині перетину лінійного проводу.

Потужність трифазного кола при з’єднанні зіркою. Активні і реактивні потужності в кожній з фаз трифазної системи можна знайти за формулами:

P_A = U_A I_A cos _A P_B = U_B I_B cos _B P_C = U_C I_C cos _C

Q_A = U_A I_A sin _A Q_B = U_B I_B sin _B Q_C = U_C I_C sin _C

Загальна потужність трифазної системи (активна і реактивна) визначається сумою потужностей окремих фаз: P = P_A + P_B + P_C; Q = Q_A + Q_B + Q_C.

При симетричному навантаженні: P_A = P_B = P_C = P_ф; Q_A = Q_B = Q_C = Q_ф; _A = _B = _C = . Тоді:

P = 3P_ф = 3 U_ф I_ф cos ; Q = 3Q_ф = 3 U_ф I_ф sin  ; S = 3U_ф I_ф.

Ці формули визначають потужність трифазної системи через фазні струми і напруги.

Іноді буває зручніше вираховувати потужність через лінійні величини струмів і напруг. Враховуючи, що при з’єднанні зіркою І_л = І_Ф і U_л = U_Ф, отримаємо

P =  U_л I_л cos 

Q =  U_л I_л sin 

S = U_л I_л

Т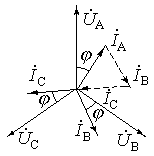 рипровідна система. При симетричному (рівномірному) навантаженні фаз, тобто, коли опори навантажень однакові Z_A = Z_B = Z_C вектори струмів в усіх фазах рівні за величиною і зсунуті відносно своїх напруг на один і той же кут .

Векторна діаграма в цьому випадку має вид:

Сума лінійних струмів дорівнює нулю, а отже струм в нульовому проводі відсутній (І_N = 0).

При симетричному навантаженні відпадає необхідність в нульовому проводі і передачу енергії від генератора до споживачів можна здійснювати по трьом проводам.

Схема трипровідної передачі має вид, наведений нижче.

Електричні мережі виконуються трипровідними тільки для живлення таких споживачів, кожний з яких створює симетричне навантаження всіх трьох фаз.

Напруги між лінійними проводами практично залишається рівними за величиною (U_AВ = U_BС = U_СА) і взаємно зсунуті по фазі на 120 як при симетричному так і при несиметричному навантаженні фаз. Фазні ж напруги в трипровідній мережі однакові за величиною тільки у випадку симетричного навантаження фаз.

Якщо в цій мережі через будь-які обставини порушується рівномірність навантаження окремих фаз, то напруга між нульовою точкою навантаження і лінійними проводами, тобто фазні напруги споживачів U_A, U_B, U_C будуть неоднакові. У зв’язку з цим встановлене раніше співвідношення U_л =  U_Ф для трипровідної системи справедливе тільки при симетричному навантаженні фаз.

При симетричному навантаженні фаз (Z_A = Z_B = Z_C = Z) розрахунок трифазного кола зводиться до розрахунку однофазного кола.

За заданим U_л визначають фазну напругу U_ф = U_л / , а потім за відомим опором навантаження Z визначають струм в проводах живлення . Зсув фаз між струмом і фазною напругою визначають за формулою cos  = R / Z.

Методика розрахунку з використанням комплексних чисел. При значній нерівномірності навантаження окремих фаз і особливо при відсутності нульового проводу симетрія напруг у споживачів порушується. В таких випадках, коли розрахунок трифазної системи не можна звести до розрахунку кіл окремих фаз з однаковими за величиною напругами, використовують символічний метод. Розглянемо схему чотирипровідної системи з урахуванням опорів проводів:

Ч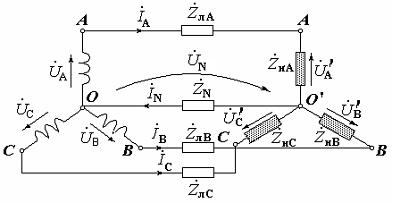 отирипровідну систему можна розглядати як складне коло з двома вузлами О і О’ і для розрахунку застосувати метод вузлових напруг.

Позначимо:

– фазні напруги на клемах генератора;

– фазні напруги на клемах навантаження;

– повні опори окремих фаз, включаючи опори лінійних проводів;

– повні провідності окремих фаз;

– опір нульового проводу;

– провідність нульового проводу.

Вважаємо, що вузловий потенціал в вузлі О дорівнює нулю. Тоді рівняння для вузла О', складене за методом вузлових напруг буде мати вид:

Вузлова напруга, тобто напруга між нульовою точкою навантаження О’ і нульовою точкою генератора О, визначається за формулою:

Далі, за методом вузлових напруг визначаються струми в вітках, тобто струми в нульовому і лінійних проводах:

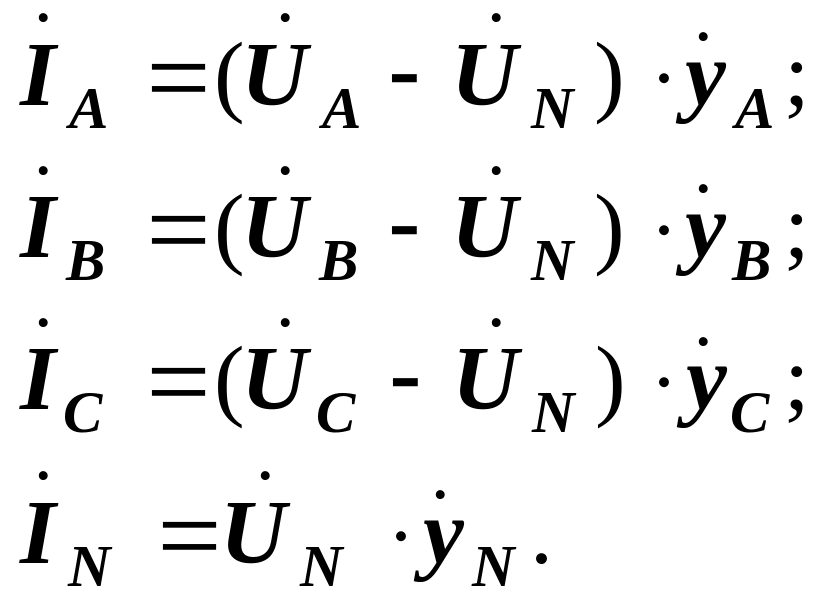
Напруги на опорах навантаження:

Нехтуючи опором лінійних проводів за попередніми формулами отримуємо співвідношення між фазними напругами генератора і навантаження:

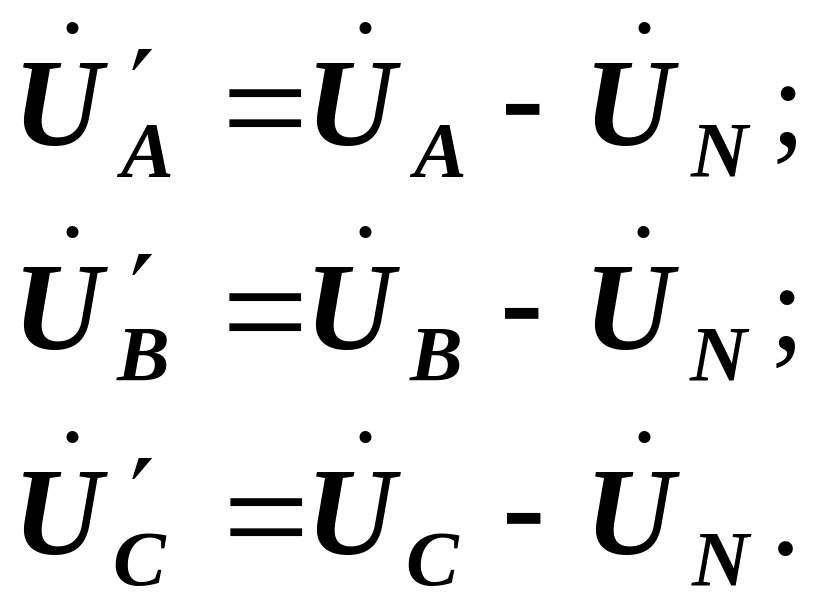
Нагадуємо, що при симетричному навантаженні напруга U_N між нульовими точками генератора і навантаження дорівнює нулю, оскільки діючі напруги U_А, U_В, U_С на клемах навантаження рівні за величиною і зсунуті по фазі на третину періоду.

Приклад. В 4–провідну мережу 3–фазного струму з лінійною напругою U_л = 220 в включені зіркою три групи ламп з опором R_А = 10 Ом, R_В = 5 Ом, R_С = 7,5 Ом. Визначити фактичні напруги на клемах ламп, що включені в фази А, В, С при обриві нульового проводу.

Розв’язання:

Оскільки опір лінійних проводів малий в порівнянні з опором ламп, можна вважати Z_A  R_А = 10 Ом; Z_B  R_В = 5 Ом; Z_С  R_С = 7,5 Ом.

Нехай вектор спрямований по дійсній осі. Тоді для фазних напруг джерела можна записати :

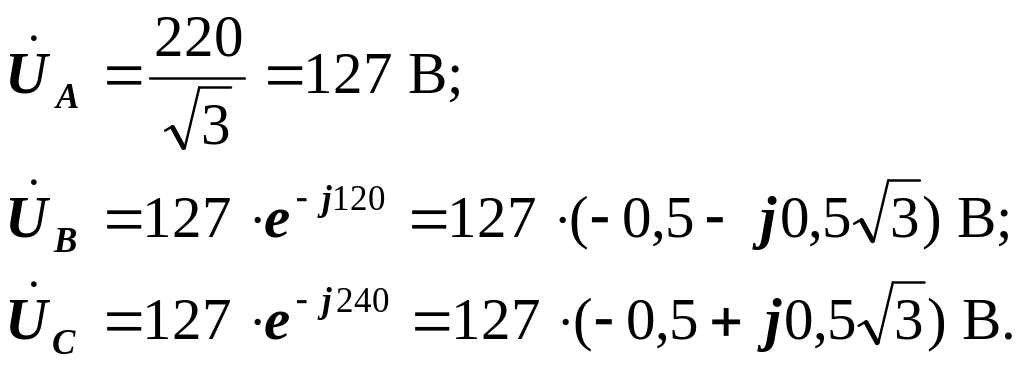
провідність окремих фаз:

При відсутності нульового проводу .

Напруга між точками О і О’:

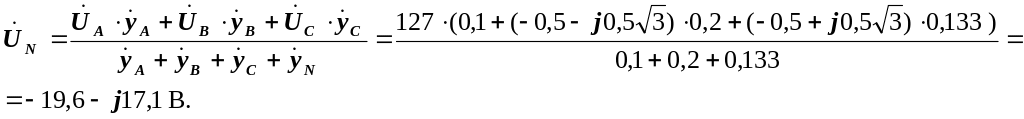
Фазні напруги на клемах навантаження:

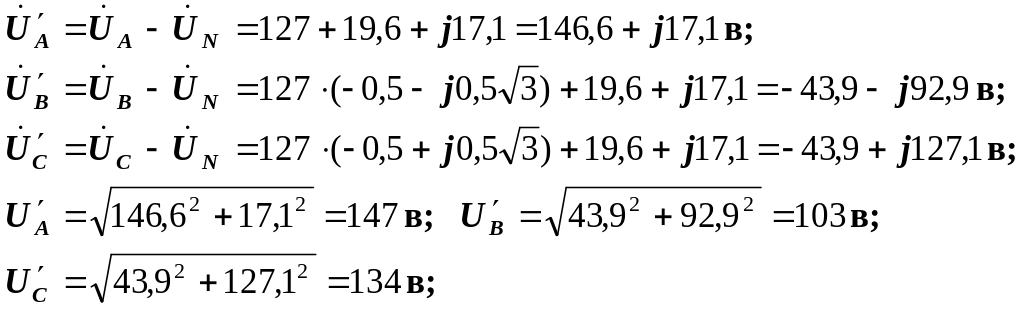
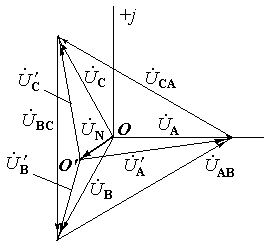
Напруги U_A' і U_В' на менш завантажених фазах перевищують номінальну напругу ламп, тому лампи, включені в фази А і С, можуть швидко перегоріти.

Векторна діаграма має вид:

Вихідна точка О відповідає нульовій точці генератора, а кінці векторів – точкам А, В, С кола. Від точки О відкладаємо вектор , кінець якого О' відповідає нульовій точці О' навантаження. Відрізки, що з’єднують на діаграмі точку О' з кінцями векторів уявляють собою вектори напруг . Вектори зображують лінійні напруги кола.

При симетричному навантаженні точка О' співпадає на діаграмі з початком векторів О. При порушенні симетрії навантаження точка О' зміщується відносно початку векторів О. Це явище має назву зміщення нейтралі.

Опір нульового проводу, як правило в багато разів менше опору навантаження будь–якої з фаз, тобто провідність нульового проводу y_N значно перевищує провідність окремих фаз y_А, y_В, y_С. Це означає, що при наявності нульового проводу величина зменшується в кілька разів, і фазні напруги в цих умовах утворюють трифазну систему, достатньо близьку до симетричної.

З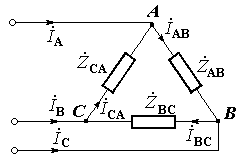 ’єднання споживачів за схемою “трикутник”. Якщо в мережу трифазного струму між кожною парою лінійних проводів А–В, В–С, С–А включити три опори Z_AB, Z_BC, Z_CA, то під дією лінійних напруг в кожному з цих опорів буде протікати струм. Такий спосіб включення навантажень в трифазну мережу має назву включення трикутником.

При з’єднанні навантажень “трикутником” по їх опорам протікають струми I_AB, I_ВC, I_CA. Ці струми називають фазними. Струми I_A, I_В, I_C, що протікають в лінійних проводах мережі називають лінійними. Показані на малюнку напрямки струмів є загальноприйнятими позитивними напрямками.

Напруга, що прикладена до опорів навантажень Z_AB, Z_BC, Z_CA прийнято називати фазними напругами U_ф. В наведеній схемі фазна напруга дорівнює напрузі між лінійними проводами, тобто лінійній напрузі U_л. Тому при з’єднанні “трикутником” U_л = U_ф .

Вибір схеми з’єднання споживачів вирішується в залежності від величини лінійної напруги мережі і номінальної напруги споживачів. В трифазних установках можливі випадки, коли одна частина споживачів з’єднана “зіркою”, а інша – “трикутником”.

З’єднання обмоток генератора за схемою “трикутник”. З’єднання “трикутником” – це коли початок кожної фазної обмотки з’єднується з кінцем наступної по порядку фазної обмотки так, що всі три обмотки утворюють замкнутий контур. В цьому контурі напрямки фазних ЕРС е_АВ, е_ВС, е_СА співпадають.

Д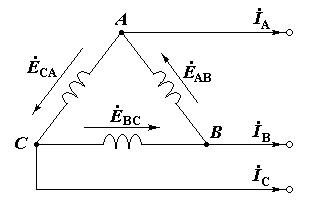 о клем А, В, С приєднується трифазна мережа, що живить навантаження. Лінійні напруги між кожною парою клем дорівнює фазній напрузі джерела (U_л = U_ф).

При відсутності навантаження струм в контурі генератора АВСА не виникає, оскільки результуюча (сумарна) ЕРС в контурі в будь–який момент часу дорівнює нулю (е_АВ + е_ВС + е_СА = 0).

Звичайно, обмотки електромашинних генераторів з’єднують зіркою. Обмотки трифазних трансформаторів, від яких живляться споживачі, прийнято з’єднувати як “зіркою”, так і “трикутником”.

Фазні і лінійні струми при з’єднанні “трикутником”. При заданій величині лінійної напруги U_л = U_ф, відомих значеннях опорів навантаження можна розрахувати фазні струми і коефіцієнти потужності окремих фаз:

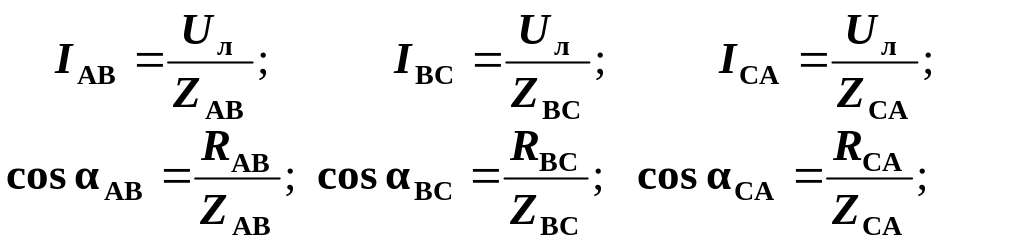
Для встановлення співвідношень між лінійними і фазними струмами складаються рівняння за першим законом Кірхгофа для точок розгалуження А, В, С, враховуючи вибрані додатні напрямки струмів:

Звідки

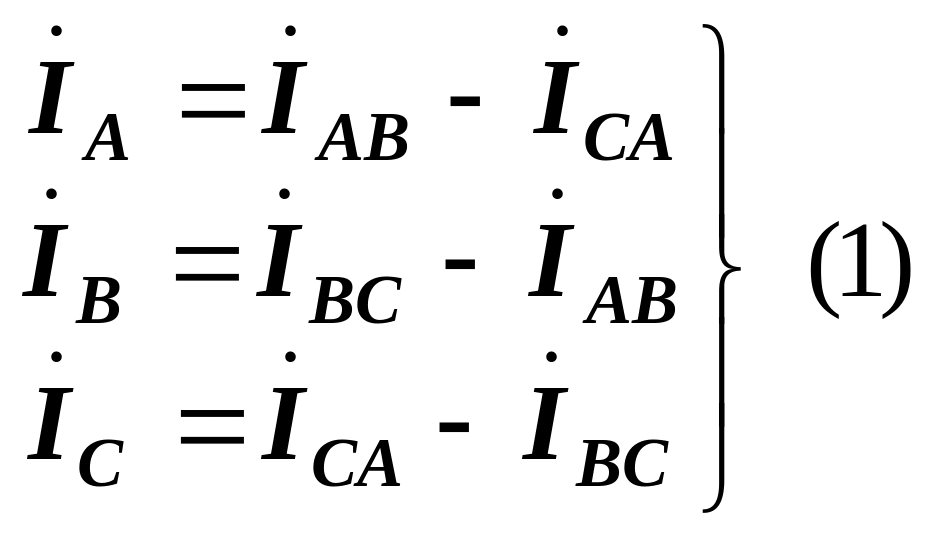
З отриманих виразів випливає, що кожний вектор лінійного струму дорівнює різниці векторів відповідних фазних струмів.

В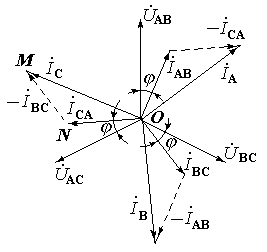 екторна діаграма напруг , фазних струмів і лінійних струмів має вид:

Складаючи праві і ліві частини рівнянь (1) отримаємо , тобто сума лінійних струмів дорівнює нулю як при симетричному, так і при несиметричному навантаженні.

При симетричному навантаженні ;  _AB =  _BC =  _CA = .

В цьому випадку лінійні струми рівні між собою і утворюють правильну трипроменеву зірку. Із рівнобедреного трикутника OMN можна знайти співвідношення між величинами лінійного і фазного струмів. При симетричному навантаженні .

Потужність трифазного кола при з’єднанні навантажень “трикутником”. В цьому випадку потужність визначається за тими же формулами, що і при з’єднані “зіркою”.

Потужність окремих фаз:

P_AB = U_ABI_ABcos _AB Q_AB = U_ABI_ABsin _AB

P_BC = U_BCI_BCcos _BC Q_BC = U_BCI_BCsin _BC

P_CA = U_CAI_CAcos _CA Q_CA = U_CAI_CAsin _CA

Загальна потужність трифазної системи визначається сумою потужностей окремих фаз

Р = P_AB + P_BC + P_CA

Q = Q_AB + Q_BC + Q_CA

При симетричному навантаженні потужності окремих фаз рівні між собою, отже

Р = 3Р_ф = 3 U_фI_фcos  ; Q = 3Q_ф = 3 U_фI_ф sin  ; S = 3 U_фI_ф

Враховуючи, що при з’єднанні “трикутником” U_л = U_ф і , можна отримати вирази потужностей через величини лінійних струму і напруги:

Р =  U_лI_лcos 

Q =  U_лI_л sin 

S =  U_лI_л

На практиці буває необхідно переключити опори навантаження із схеми “трикутник” на схему “зірка”, наприклад, переключення трифазних електропечей з метою регулювання їх потужності, а, відповідно і температури. Потужність, що споживається при з’єднанні “трикутником”, буде при тій же напрузі мережі в тричі більшою за потужність, що споживається цими ж опорами при з’єднанні “зіркою”. Дійсно, при з’єднанні “зіркою”

,

а при з’єднанні “трикутником”

,

звідки .

Приклади виконання розрахункових завдань

Приклад 1. Визначити розподіл струмів і напруг в простому колі змінного струму. Побудувати векторну діаграму.

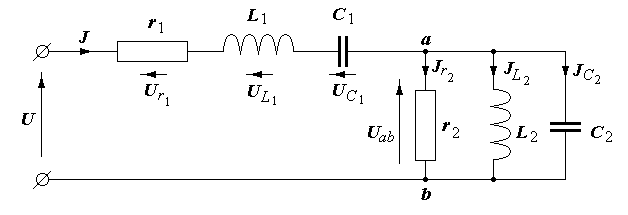
Вихідні дані:

r₁ = 6 Ом; L₁ = 25,5 мГ; С₁ = 1590 мкф; r₂ = 5 Ом; L₂ = 5 мГ; С₂ = 1000 мкф; U = 127 В; f = 50 Гц.

Розрахунок:

1. Визначаємо Z₁ – повний опір з’єднаних послідовно елементів r₁, L₁, С₁:

X_L1 = 2π f·L₁ = 2·3,14·50·25,5·10^–3 = 8 Ом;

Х_C1 = 1/(2π f·С₁) = 1/(2·3,14·50·1590·10^–6) = 2 Ом;

2. Визначаємо y₂ – повну провідність⁶ паралельної частини схеми:

X_L2 = 2π f·L₂ = 2·3,14·50·5·10^–3 = 1,57 Ом;

Х_С2 = 1/(2π f·С₂) = 1/(2·3,14·50·1000·10^–6) = 3,18 Ом;

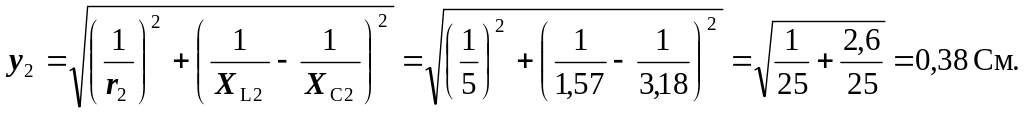
3. Знаходимо повний опір схеми (Z), струм (J) і напруги (U_r1, U_L1, U_C1, U_аb):

Z = Z_l + Z₂ = Z_l + l / y₂ = 8,5 + 2,63 = 11,13 Ом;

J= U / Z= 127 / 11,13 = 11,4 А;

U_r1= J·r₁ = 11,4·6 = 67,3 В;

U_L1 =J·X_L1 = 11,4·8 = 91 B;

U_C1 = J·X_C1= 11,4·2 = 22,8 В;

U_ab = J·Z₂= 11,4·2,63 = 30 В;

4. Визначаємо струми у вітках розгалуженої частини схеми:

J_r2 = U_ab /r₂ = 30 / 5 = 6 А;

J_L2 = U_ab / X_L2 = 30 /1,57 = 19,1 А;

J_C2 = U_ab / X_C2 = 30 / 3,18 = 9,4 А;

5. Визначаємо зсув фаз між напругою U_ab і струмом J:

b_L2 = 1/ Х_L2 = 1 / 1,57 = 0,64; b_С2 = 1 / Х_С2 = 1 /3,18 = 0,315;

φ = arcsin (b / y) = arcsin ((b_L2 – b_C2) / y₂) = arcsin (0,335 / 0,38) = arcsin 0,885  φ = 62°.

6. Будуємо векторну діаграму струмів і напруг схеми, для чого обираємо масштаби струмів і напруг: т_j = 0,4:1 А/мм; т_U= 4:1 В/мм.

За базовий обираємо вектор струму J, оскільки він є спільним для послідовної і паралельної частин схеми, і відкладаємо його у відповідному масштабі по горизонталі⁷.

В 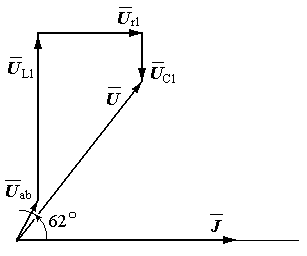раховуючи індуктивний характер розгалуженої частини кола (b_L2 > b_C2), відкладаємо під кутом φ = 62° вектор напруги .

У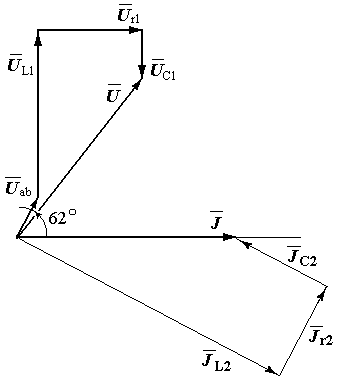 відповідності з рівнянням будується векторна діаграма напруг з урахуванням кутів зсуву фаз між струмом i напругами на елементах. Вектор напруги випереджає вектор струму на 90°, вектор напруги співпадає за напрямком з вектором струму , а вектор напруги відстає від вектора струму на 90°:

Потім будується векторна діаграма струмів. Для цього за базисний приймається вектор , спільний для паралельної частини схеми, і відносно нього будуємо діаграми струмів, використовуючи формулу i фазові співвідношення між відповідними величинами:

Приклад 2. Розрахунок складних кіл змінного струму.

Використовуючи метод суперпозиції, визначити струми у вітках наведеного кола. Параметри елементів кола: R₁ = 12 кОм, R₂ = 10 к0м, R₃ = 0,2 кОм, L₁ = 0,5 мГн, L₂ = 12 мГн, Е₁ = 80 В, Е₂ = 120 В, ω = 5·10⁶ с^–1.

Розрахунок в середовищі MathCAD⁸:

Вихідні дані:

R₁ := 12000 R₂ := 10000 R₃ := 200 L₁ := 0.5·10^–3 L₂ := 12·10^–3 E₁ := 80·e ^j·0 E₂ := 120·e ^j·0 ω := 5·10⁶

Визначаємо комплексні опори віток:

Z₁ := R₁ Z₂ := R₂ + j·ω·L₁ Z₃ := R₃ + j·ω·L₂

a) Знаходимо струми у вітках при відсутності джерела Е₂:

Струм у вітці, що містить R₁:

Струм у вітці, що містить R₂:

Струм у вітці, що містить R₃:

б) Знаходимо струми у вітках при відсутності джерела Е₁:

Струм у вітці, що містить R₂:

Струм у вітці, що містить R₁:

Струм у вітці, що містить R₃:

Фактичний струм у вітках:

Струм у вітці, що містить R₁: І₁ := І_1а + І_1b I₁ = –1.6410^–3 – 5.554j10^–4

Струм у вітці, що містить R₂: І₂ := І_2а + І_2b I₂ = 1.75610^–3 – 1.105j10^–3

Струм у вітці, що містить R₃: І₃ := І_3а + І_3b I₃ = –1.16610^–4 + 1.661j10^–3

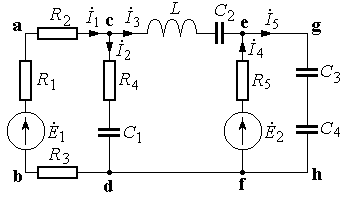
Приклад 3. Використовуючи метод контурних струмів визначити розподіл струмів у вітках наведеної схеми:

Розрахунок проводиться в середовищі MathCAD:

ORIGIN := 1

Вихідні дані:

R₁ := 1000 R₂ := 1000 R₃ := 2000 R₄ := 800 R₅ := 4000

С₁ := 1·10^–9 С₂ := 2·10^–9 С₃ := 0.5·10^–9 С₄ := 0.4·10^–9 L := 4·10^–3

Е₁ := 80·е ^j·0 Е₂ := 120·е ^j·π / 4 ω := 5·10⁶

Схема включає три контури: acdba, cefdc, eghfe.

Матриця коефіцієнтів розрахункової системи рівнянь:

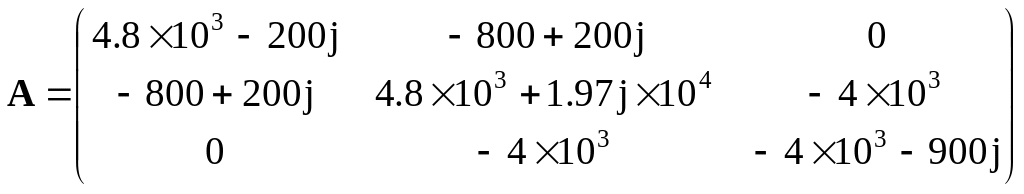
Вектор правих частин розрахункової системи рівнянь:

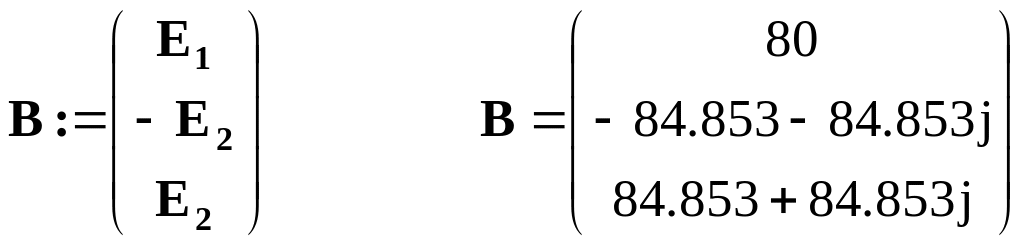
Розв’язання системи рівнянь відносно контурних струмів:

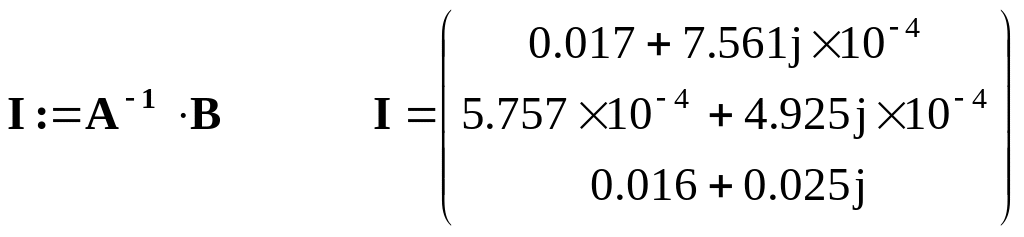
Комплексні зображення струмів у вітках⁹:

І₁ := І₁ І₂ := І₁ – І₂ І₃ := І₂ І₄ := І₃ – І₂ І₅ := І₃

І₁ = 0.017 + 7.561j  10^–4 I₂ = 0.016 + 2.636j  10^–4

І₃ = 5.757  10^–4 + 4.925j  10^–4 І₄ = 0.016 + 0.025j І₅ = 0.016 + 0.025j

Аналітичні вирази для струмів у вітках¹⁰ (i = І_m·sin(ωt + ψ):

|I₁| = 0.017 і₁ = 0.017·sin(5·10⁶·t + 2,547°)

|I₂| = 0.016 і₂ = 0.016·sin(5·10⁶·t + 0,944°)

|I₃| = 7.576E–4 і₃ = 7.576E–4·sin(5·10⁶·t + 40,546°)

|I₄| = 0.03 і₄ = 0.03·sin(5·10⁶·t + 57,381°)

|I₅| = 0.03 і₅ = 0.03·sin(5·10⁶·t + 57,381°)

П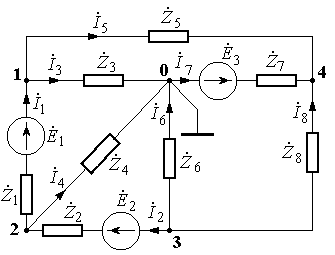 риклад 4. Використовуючи метод вузлових напруг визначити розподіл струмів у вітках схеми:

Розрахунок проводиться в середовищі MathCAD:

ORIGIN := 1

Вихідні дані:

Матриця коефіцієнтів розрахункової системи рівнянь:

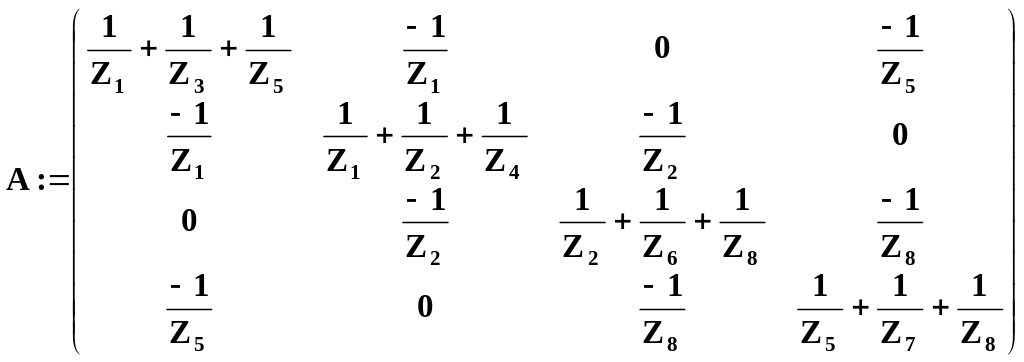
Матриця правих частин розрахункової системи рівнянь:

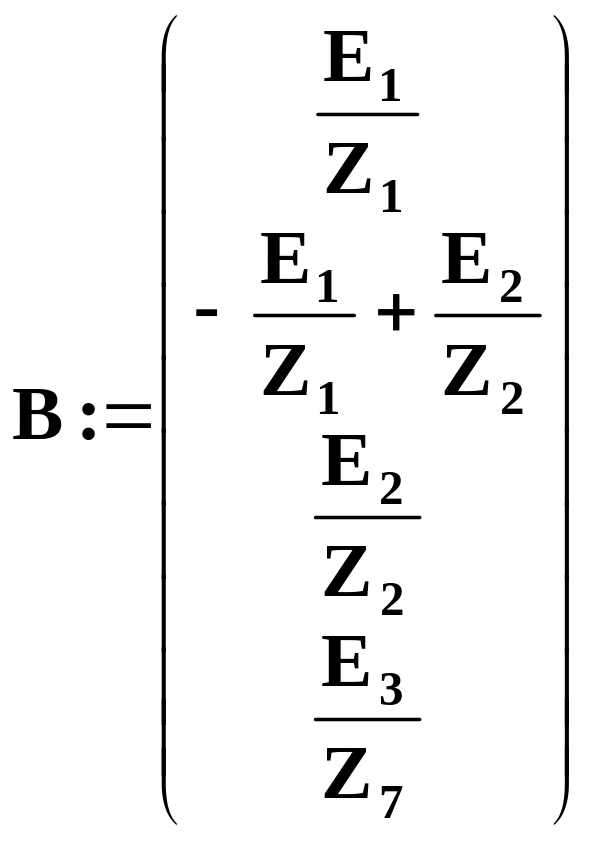
Розв’язання розрахункової системи рівнянь AU = B.

Струми у вітках:

I₁ = 0.012 + 0.026j I₂ = –0.101 – 0.05j I₃ = 0.022 + 0.012j I₄ = 0.032 – 7.91j10^–3 I₅ = –0.01 + 0.013j I₆ = –0.028 – 0.031j I₇ = 0.026 – 0.026j I₈ = –0.016 + 0.013j

Аналітичні вирази для струмів у вітках визначаються так же, як і в попередньому прикладі.

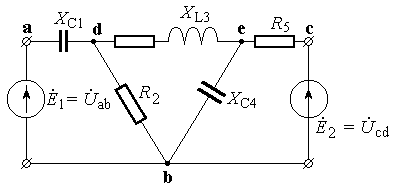
Приклад 5. Представлена схема кола, що зустрічається в релейному захисті (фільтр-реле зворотної послідовності).

Задано: Х_С1 = Х_С4 = 260 Ом; R₂ = 450 Ом; R₃ = 173 Ом; R₅ = 150 Ом; Х_L3 = 300 Ом. До клем a–b і c–d прикладена напруга U_ab = U_cd = 10 В, причому напруга U_cd відстає за фазою від напруги U_ab на π/3.

Визначити напругу U_de (напруга на клемах реле) і струм у вітці de.

Розрахунок. Розглянемо вітку de як навантаження, а решту кола як активний двополюсник.

Вхідний опір активного двополюсника:

Визначаємо напругу холостого ходу :

Струм у вітці de:

Напруга :

Приклад 6. До трифазної мережі із лінійною напругою U_л = 220 В підключене симетричне навантаження, з’єднане за схемою «трикутник». Активний опір фази R_ф = 4 Ом, реактивний індуктивний – Х_ф = 3 Ом. Визначити фазні і лінійні струми і напруги в таких режимах:

в симетричному трифазному;

2) при обриві однієї фази;

3) при обриві лінійного проводу.

Побудувати для всіх режимів векторні діаграми струмів і напруг.

Р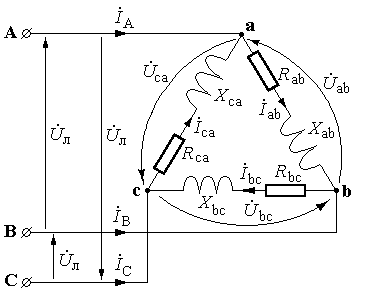 озрахунок.

1) Симетричний режим (див. рис.).

Визначаємо комплексні вирази для фазних опорів і напруг:

Z_ф := 4 + 3·j

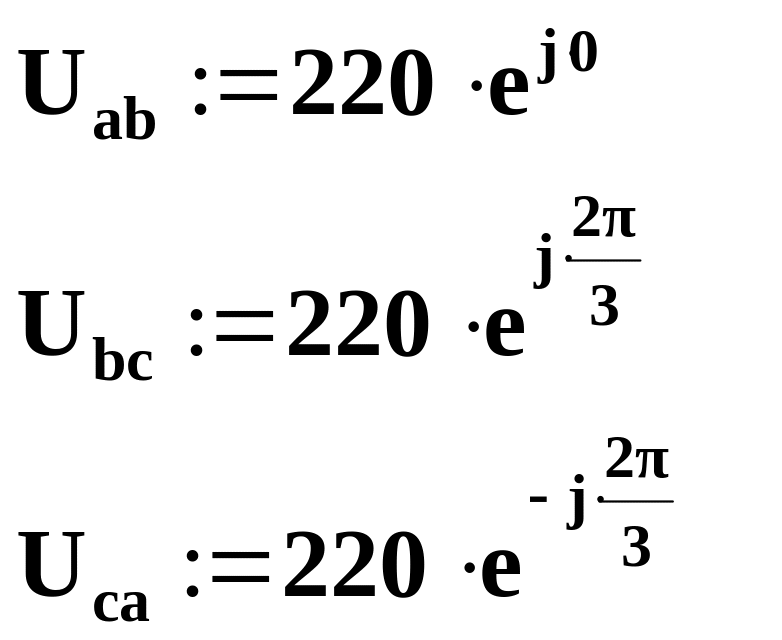
Знаходимо комплексні вирази для фазних струмів:

Знаходимо комплексні вирази для лінійних струмів:

I_A := I_ab – I_ca I_A = 75.663 – 9.116 j

I_B := I_bc – I_ab I_B = –29.937 + 70.084 j

I_C := I_ca – I_bc I_C = –45.726 – 60.958 j

Векторна діаграма напруг і струмів має вид:

2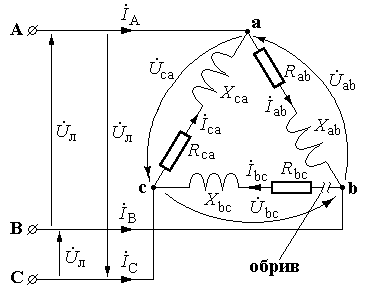 ) Обрив однієї фази (див. рис.).

При обриві фази навантаження bc струм . Струми і залишаються без змін, тому колишнє значення має і струм . Струми і змінюються: .

Векторна діаграма струмів матиме вид:

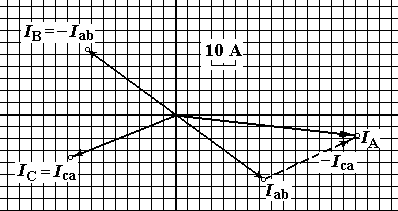
3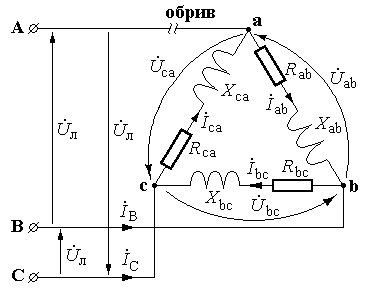 ) Обрив лінійного проводу (див. рис.).

При обриві лінійного проводу А–а опори у вітках са і ab виявляються з’єднані послідовно. Отже, на кожний з цих опорів припадає половина лінійної напруги U_BC, оскільки опори у вітках са і ab однакові (Z_ф). Визначаємо комплексні вирази для лінійних напруг, що прикладені до опорів віток у випадку обриву лінійного проводу:

Приймаємо , тоді: за другим законом Кірхгова для контура abc ,

звідки .

Знаходимо комплексні вирази для фазних струмів:

Знаходимо комплексні вирази для лінійних струмів:

Векторні діаграми напруг і струмів матимуть вид:

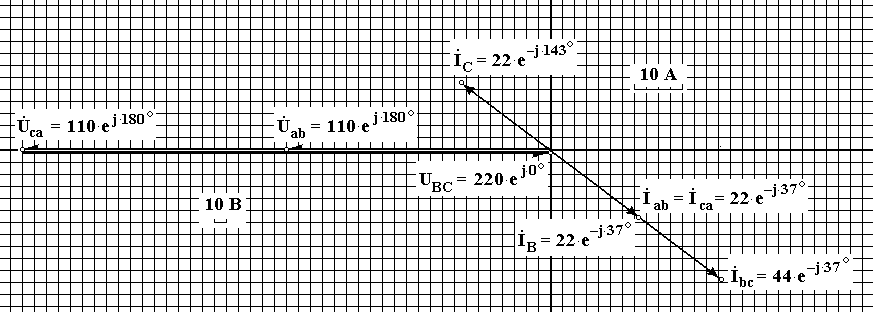
Приклад 7. До трифазної лінії з лінійною напругою U_л = 380 В підключене несиметричне навантаження, з’єднане за схемою «зірка» з нейтральним проводом. Активні і реактивні опори фаз навантаження R_а = 10 Ом, Х_а = 0; R_b = 3 Ом, Х_b = 4 Ом; R_с = 9 Ом, Х_с = –12 Ом.

Опір нейтрального проводу нехтовно малий. Визначити фазні і лінійні струми і напруги в таких режимах:

1) трифазному;

2) при обриві лінійного проводу;

3) при короткому замиканні фази навантаження і обриві лінійного проводу.

Побудувати для всіх режимів векторні діаграми струмів і напруг.

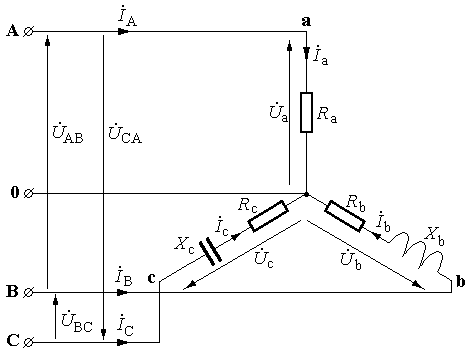
Розрахунок.

1) Несиметричний трифазний режим (див. рис.).

Визначаємо комплексні вирази для фазних напруг:

Знаходимо фазні струми:

Вираховуємо струм в нульовому проводі:

Знаходимо лінійні напруги:

Векторна діаграма струмів і напруг матиме вид:

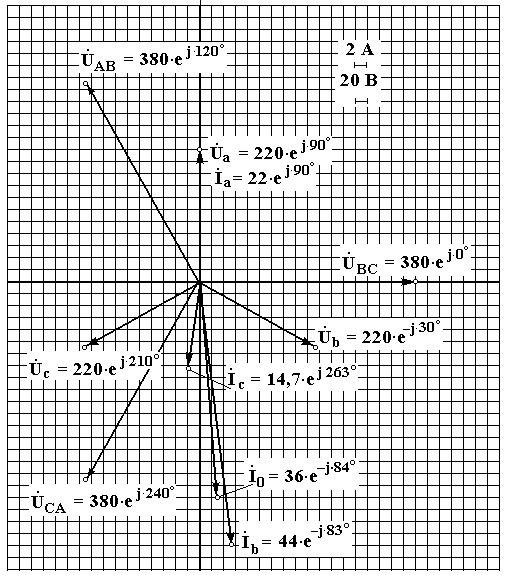
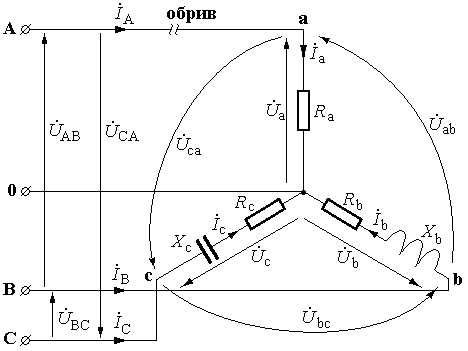
2) Обрив лінійного проводу (див. рис.).

При обриві лінійного проводу А–а струм І_А у фазі А відсутній, тобто струм І_а  = 0; струми І_b і І_c мають такі ж напрямки, як і у трифазному режимі.

Струм у нульовому проводі:

Фазна напруга U_a відсутня (U_a = 0); напруги U_b і U_c направлені як і трифазному режимі.

Знаходимо лінійні напруги на навантаженнях при обриві лінійного проводу А–а:

Векторна діаграма струмів і напруг матиме вид:

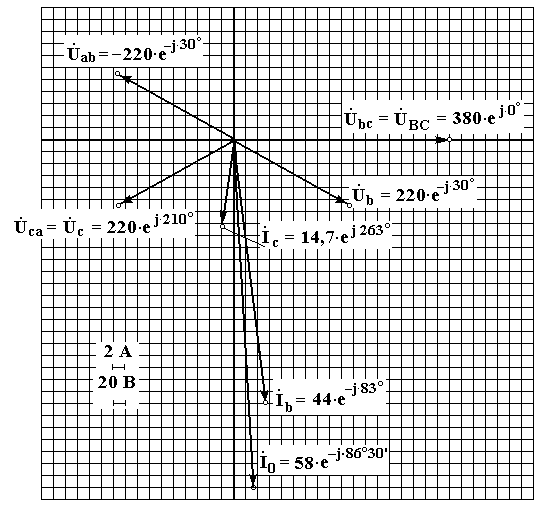
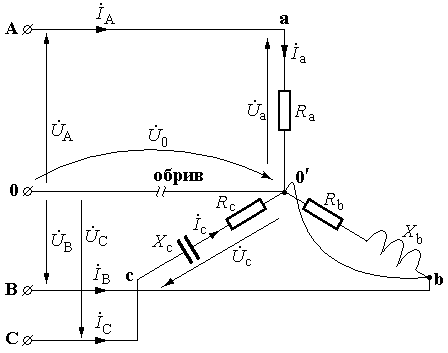
3) Коротке замикання фази навантаження і обрив нейтрального проводу (див. рис.).

Запишемо вирази для фазних напру мережі:

Знаходимо напругу U₀:

Визначаємо фазні напруги на навантаженнях при заданому режимі:

звідки

звідки

Знаходимо фазні струми:

В екторна діаграма струмів і напруг: