Исходные данные для задачи 3

Номер варианта					Номер варианта
1	80	0,2	0,2	3	16	50	0,3	0,8	1
2	120	0,7	0,6	3	17	110	0,3	0,9	7
3	50	0,6	0,5	15	18	90	0,1	0,9	18
4	50	1	0,9	14	19	140	0,7	0,6	9
5	60	0,6	0,7	3	20	80	0,5	0,2	10
6	120	0,4	0,4	8	21	110	0,9	0,5	9
7	90	0,3	1	8	22	80	0,2	0,5	13
8	130	1	0,2	6	23	50	0,5	0,9	11
9	70	1	0,2	8	24	140	0,6	1	1
10	100	0,2	0,5	13	25	70	0,7	0,5	1
11	110	0,2	0,5	15	26	120	0,3	0,2	8
12	80	0,2	0,8	16	27	90	0,5	0,6	14
13	90	0,3	0,3	9	28	140	0,3	0,9	15
14	110	0,3	0,9	0	29	90	0,2	0,7	8
15	120	0,2	0,2	11	30	80	0,6	0,3	1

4. Разрешение конфликта между предприятиями

В некотором городе имеются два предприятия, которые могут выпускать продукцию разных типов, но одного и того же назначения. Предприятие планирует выпускать продукцию двух типов и , а предприятие – типов и . Сбыт продукции одного предприятия зависит от того, какую продукцию выпускает другое предприятие. Специалисты по прогнозированию спроса установили, что если предприятие выпустит единицу продукции типа , а предприятие – единицу продукции типа , то ожидаемые доходы предприятий от реализации единицы продукции будут равны и ден.ед. соответственно. Таким образом, между предприятиями имеет место конфликт, поскольку каждое из них стремится максимизировать свой ожидаемый доход. Этот конфликт моделируется биматричной игрой предприятий и с платежными матрицами:

, .

Требуется определить пропорции в типах продукции, которые целесообразно выпускать каждому предприятию для максимизации ожидаемого дохода.

Методические указания

1. Представить задачу в виде биматричной игры двух игроков.

2. Определить стратегию равновесия по Нэшу. Найти максимальный ожидаемый доход для каждого предприятия. Можно использовать при этом ЭТ Excel.

3. Определить оптимальные пропорции в выпускаемой продукции каждым предприятием.

Рекомендуемая литература: [1, С. 108–114].

Исходные данные приведены в табл. 4.3.

Пример решения задачи

Пусть , , , , , , , . Имеем биматричную игру двух игроков (предприятий и ) с платежными матрицами:

, .

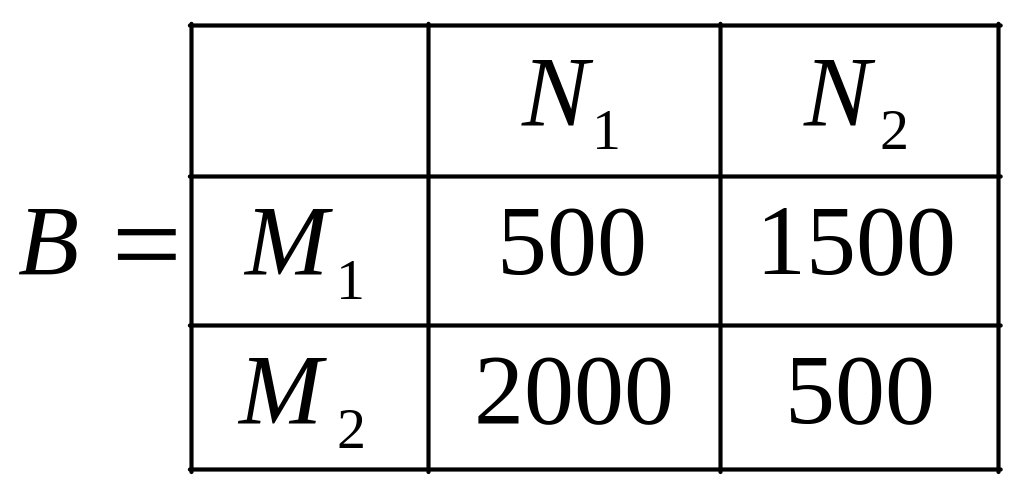Пусть – стратегия игрока , а – стратегия игрока . По теореме Нэша каждая биматричная игра имеет, по крайней мере, одну ситуацию равновесия. Это значит, что существуют стратегии и , для которых справедлива система неравенств

,

где

, ,

, .

Для данных задачи получим

, ,

, ,

и система неравенств принимает вид

.

Если , то из первого неравенства следует, что , а из третьего неравенства следует, что , а это противоречивые неравенства.

Если , то из второго неравенства следует, что , а из четвертого неравенства следует, что , а это также противоречивые неравенства.

Следовательно, . Тогда из первых двух неравенств следует, что . А из третьего и четвертого неравенств следует, что .

Таким образом, ситуацию равновесия в смешанных стратегиях образуют векторы: и .

Математические ожидания выигрышей игроков в ситуации равновесия равны:

и

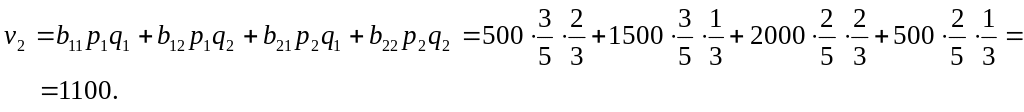
Полученное решение в содержательных терминах примера означает, что предприятие выбирает выпуск продукции и с вероятностями, соответственно равными 3/5 и 2/5, а предприятие – выпуск продукции и с вероятностями 2/3 и 1/3. При этом математическое ожидание дохода предприятия будет равно 500 ден.ед., а предприятия – 1100 ден.ед.

Оптимальные пропорции выпуска продукции: для предприятия 60% продукции и 40% продукции , для предприятия 67% продукции и 33% продукции .

Определим ситуацию равновесия в биматричной игре с помощью Excel. На рис. 4.1 представлен образец записи исходных данных.

Таблица 4.1

	A	B	C	D		E
1	Равновесие в биматричной игре 2х2
2
3	A			B
4	600	300		500		1500
5	300	900		2000		500
6
7	Неизвестные векторы			Сумма
8	Строка P	0	0	0
9
10	Столбец Q	0		0
11		0
12
13	Условия равновесия Нэша
14		AQ	<=	PAQ
15		0		0
16		0
17
18	PB		<=	PBQ
19	0	0		0

В ячейках A4 : B5 записаны элементы матрицы , а в ячейках D4 : E5 – элементы матрицы . Для компонент искомых векторов и зарезервированы ячейки B8 : C8 и B10 : B11 соответственно. В ячейках D8 и D10 помещаются суммы компонент этих векторов (см. табл. 4.2).

Таблица 4.2

Ячейка	Формула
D8	=СУММ(B8:C8)
D10	=СУММ(B10:B11)

Условия равновесия Нэша можно представить в матричном виде

.

есть вектор-столбец, компоненты которого расположены в ячейках B15:B16. Чтобы вычислить эти компоненты, следует выделить соответствующие ячейки и обратиться к функции «МУМНОЖ», указав адрес матрицы A и адрес вектора Q:

{=МУМНОЖ(A4 : B5; B10: B11)}.

Одновременное нажатие клавиш Ctrl + Shift + Enter приведет к заполнению выделенных ячеек. есть число, полученное умножением строки на столбец . Поэтому в ячейку D15 заносится формула

=МУМНОЖ(B8 : C8; B15 : B16).

есть вектор-строка, компоненты которой расположены в ячейках A19:B19. Чтобы вычислить эти компоненты, следует выделить соответствующие ячейки и обратиться к функции «МУМНОЖ», указав адрес строки P и адрес матрицы B:

{=МУМНОЖ(B8 : C8; D4 : E5)}.

Одновременное нажатие клавиш Ctrl + Shift + Enter приведет к заполнению выделенных ячеек. есть число, полученное умножением строки на столбец . Поэтому в ячейку D19 заносится формула

=МУМНОЖ(A19 : B19; B10 : B11).

Обращение к процедуре “Поиск решения” показано на рис. 4.1.

Рис. 4.1.

За целевую ячейку принята D8, значение которой должно быть равно 1, поскольку . Неизвестными являются компоненты векторов и , расположенные в ячейках B8 : C8 и B10 : B11. Условия равновесия записываются в виде ограничений B15 : B16 <= D15 и A19 : B19 <= D19. Ограничения B8 : C8 >= 0 и B10 : B11 >= 0 представляют собой условия неотрицательности векторов и . Ограничение D10 = 1 соответствует условию нормировки вектора : .

Выполнение процедуры “Поиск решения” приводит к нахождению стратегий равновесия игрока : , (ячейки B8 : C8) и игрока : , (ячейки B10 : B11), а также к средним ожидаемым выигрышам игрока : (ячейка D15) и игрока : ( ячейка D19).

Таблица 4.3