3. Выбор оптимальной стратегии движения

Молодая девушка часто ездит между двумя городами. При этом есть возможность выбрать один из двух маршрутов: маршрут представляет собой скоростное шоссе в три полосы, маршрут – длинную однополосную дорогу. Патрулирование дорог осуществляется ограниченным числом машин ДПС. Если все машины расположены на одном маршруте, девушка с ее страстным желанием ездить очень быстро, несомненно, получит штраф за превышение скорости в размере ден.ед. Если машины патрулируют на двух маршрутах в соотношении 50 на 50, то с вероятностью девушка получит штраф в размере ден.ед. на маршруте и с вероятностью она получит такой же штраф на маршруте . Кроме того, маршрут длиннее, поэтому бензина расходуется на ден.ед. больше, чем на маршруте . Определить стратегию выбора оптимального маршрута как для девушки, так и для ДПС.

Методические указания

1. Представить задачу в виде матричной игры с нулевой суммой.

2. Решить задачу графически.

3. Составить пару симметричных двойственных задач линейного программирования. В Excel найти оптимальные решения этих задач. Определить оптимальные стратегии игроков и цену игры.

Рекомендуемая литература: [1, С. 85–105].

Исходные данные приведены в табл. 3.4.

Пример решения задачи

Пусть , , , .

Чистые стратегии игрока (молодой девушки):

– выбор маршрута с тремя полосами,

– выбор маршрута с одной полосой.

Чистые стратегии игрока (ДПС):

– патрулирование на маршруте с тремя полосами,

– патрулирование на маршруте с одной полосой,

– патрулирование на двух маршрутах.

Матрица игры имеет вид

	–100	0	–50
	–15	–115	–45

Рассмотрим сначала графический метод решения игры. Оптимальной является такая стратегия игрока , для которой функция

максимальна. Полагая последовательно , и , получим следующую задачу максимизации:

.

Так как , то эту задачу можно записать в виде:

(3.1)

при условии .

Эта задача нелинейной оптимизации решается графически, как показано на рис. 3.1. Для этого на отрезке изобразим три прямые линии с уравнениями

(1): ,

(2): ,

(3): .

Тогда график функции (3.1) представляет собой выделенную на рис. 3.1 ломаную линию. Максимальное значение этой функции можно найти, решив систему уравнений, составленную из (1)-го и (2)-го уравнений. Тогда . Отсюда находим

, , .

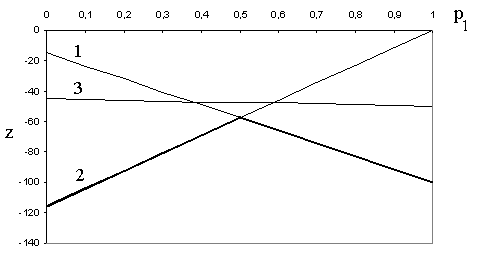
Рис. 3.1. Графический метод решения

Так как точка максимума лежит на пересечении 1-й и 2-й прямых, то стратегия не входит в оптимальную стратегию игрока . Таким образом, и мы можем найти его оптимальную стратегию при помощи матрицы . Для игры порядка получим , . Следовательно, .

Рассмотрим теперь метод решения игры с помощью линейного программирования. Поскольку платежная матрица содержит отрицательные выигрыши, то ко всем ее элементам следует прибавить одно и то же число такое, чтобы все элементы матрицы стали неотрицательными. Возьмем в качестве такого числа . Тогда получим игру с новой матрицей

	15	115	65
	100	0	70

Исходная и двойственная задачи представлены в табл. 3.1.

Таблица 3.1

Задача I	Задача II
Найти числа такие, что	Найти числа такие, что
при ограничениях	при ограничениях

Решение этих задач легко получить в Excel. Расположение данных для задачи I приведено в табл. 3.2.

Таблица 3.2

	A	B	C	D	E	F	G
1	Матричная игра с нулевой суммой
2
3					ЦФ	Экстремум
4	Неизвестные				0	Максимум
5		Ограничения
6					Левая часть	Знак	Правая часть
7	1 маршрут	15	115	65	1	<=	1
8	2 маршрут	100	0	70	1	<=	1

В ячейках E4, E7, E8 содержатся формулы из табл. 3.3.

Таблица 3.3

Ячейка	Формула
E4	=СУММ(B4:D4)
E7	=СУММПРОИЗВ(B4:D4;B7:D7)
E8	=СУММПРОИЗВ(B4:D4;B8:D8)

Обращение к процедуре «Поиск решения» показано на рис. 3.2.

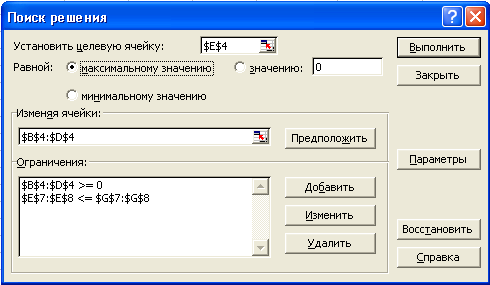
Рис. 3.2.

В результате оптимизации получим значения неизвестных: (ячейка B4), (ячейка С4), (ячейка D4) и значение целевой функции (ячейка E4).

Решение задачи II можно определить аналогичным образом путем обращения к процедуре «Поиск решения». Однако это решение, именуемое как теневые цены, можно найти также из «отчета по устойчивости»: , .

Находим решение игры. Цена игры с новой матрицей:

.

Оптимальная стратегия игрока определяется по формуле: , следовательно,

.

Оптимальная стратегия игрока определяется по формуле: , следовательно,

.

Цена игры с исходной матрицей:

ден.ед.

Согласно стратегии молодая девушка должна выбирать маршруты движения с одинаковыми вероятностями. При этом ее выигрыш составит ден.ед.

Наихудшая для нее стратегия ДПС состоит в том, что с вероятностью 0,575 будет патрулирование трехполосного маршрута и с вероятностью 0,425 будет патрулирование однополосного маршрута.

Таблица 3.4