1.4. Інтегральні формули векторного аналізу.

Приведемо найважливіші для теорії електромагнетизму інтегральні співвідношення без доведення.

Теорема Остроградського-Гаусса.

де S – поверхня, яка охоплює об’єм V.

Теорема Стокса

де L – контур, на який “натягнута” поверхня S.

Задачі до §1.

1. Обчислити величину і напрямок градієнта поля в точках О(0,0,0), А(1,1,1), В(2,0,1). В якій точці градієнт дорівнює нулю?

2. Знайти кут φ між градієнтами поля в точках А(1,2,2) та В(-3, 1,0).

3. Довести .

4. Знайти , де .

5. Знайти дивергенцію поля в точці М(3,4,5). Чому наближено дорівнює потік П вектора через нескінченно малу сферу .

Розв’язання:

За означенням дивергенції: . Виконуємо підстановку компо-нент вектора , отримуємо: . Остаточно - 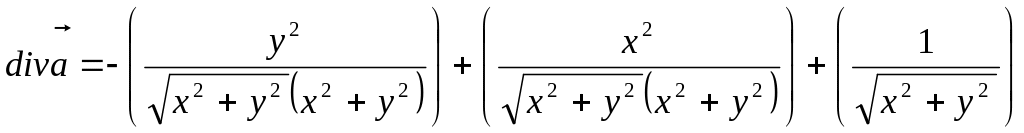, . Підстановка координат точки дозволяє отримати чисельне значення дивергенції у цій точці: .

За означенням потік вектора через деяку замкнену поверхню S визначається співвідношенням: . Застосуємо формулу Остроградського, отримуємо: .Оскільки потік пронизує нескінченно малу сферу із центром у т. М(3,4,5), то можна покласти, що в межах сфери . Тому шукана величина рівна , де V-об’єм сфери. Остаточно отримуємо .

5. Довести тотожність .

6. Обчислити , де . У якому випадку ?

7. Знайти циркуляцію вектора (с=const) вздовж кола , .

8. Обчислити ротор векторного поля у точці М(1,1,2).

9. Знайти рівняння силових ліній поля, яке описується наступною векторною функцією: , де - орт полярної системи координат.

Розв’язання:

У декартовій системі відліку задана векторна функція має наступні компоненти: . Підставимо компо-ненти векторної функції у рівняння силових ліній, отримуємо: , або . Інтегрування останньої рівності приводить до співвідношення виду , де С – довільна стала. Остаточно отримуємо: . Таким чином, силовими лініями заданого поля є сукупність променів, які виходять із спільного центру.

Контрольні запитання до §1.

1. Розкрийте зміст поняття поля.

2. Які існують типи полів?

3. Дайте означення операцій градієнта, дивергенції, ротора.

4. Якими є ознаки потенціальних полів?

5. Якими є ознаки соленоїдальних полів?

6. Запишіть співвідношення для розрахунку градієнта, дивергенції, ротора у декартовій системі відліку.

7. Розкрийте фізичний зміст операцій градієнта, дивергенції, ротора.

§2. Заряди, струми, електромагнітні поля.

2.1. Заряди та струми.

Поняття заряду є одним із основоположних понять теорії електромагнетизму. Заряд (q,[Кл]) – це фізична скалярна величина, яка визначає міру взаємодії заряджених тіл. Заряд величина дискретна. Найменшою одиницею заряду є заряд електрона Кл.

Матеріальні тіла складаються із мікрооб’єктів – атомів, що мають позитивно заряджене ядро і негативно заряджену електронну хмару. За нормальних умов позитивні і негативні заряди в речовині урівноважені. Це означає, що більшість об’єктів макросвіту проявляє електронейтралні властивості. Порушення рівноваги приводить до появи на матеріальному об’єкті надлишкового позитивного чи негативного заряду, яка пропорційна заряду електрона.

У класичній теорії електромагнетизму (макроскопічній теорії) розглядають явища, які спричинені дією великої кількості заряджених частинок. При цьому дискретність заряду втрачає зміст. Тому при розв’язанні практичних задач використовується наближення (чи ідеалізація) неперервності заряду.

Границю виду:

,

де - кількість заряду, яка знаходиться в об’ємі , називають густиною заряду. У ідеалізованих середовищах для визначення величини ρ виправданим є використання співвідношення:

.

Сукупність заряджених частинок може перебувати у поступальному русі. При цьому утвориться потік заряджених частинок, який називається струмом провідності. Струм (І) – це фізична векторна величина, яка вимірюється в Амперах [А] і визначається кількістю заряду , що проходить через одиницю поверхні за час :

,

або при переході до диференціальної форми запису:

,

де – орт, який визначає напрямок протікання струму (вектор нормалі до поверхні).

Густиною струму називається векторна величина, яка визначається співвідношенням:

,

де – елементарна поверхня, яка перпендикулярна до напрямку протікання струму .

Один із фундаментальних законів природи – закон збереження заряду. Згідно із цим законом заряд не зникає безслідно і не виникає з нічого. Нехай в деякому об’ємі V, який обмежено поверхнею S міститься заряд q. Якщо заряд не залишається постійним з плином часу, тобто його величина зменшується або збільшується у об’ємі V, то ці зміни можна пояснити лише переходом носіїв заряду через поверхню S. З іншого боку, якщо через поверхню S проходить струм, то його величина повинна пов’язуватись із зміною заряду:

.

Отримали формальне визначення закону збереження заряду у інтегральному вигляді. Струм, що проходить у середину виділеного об’єму вважають від’ємним (при цьому величина заряду q в об’ємі збільшується, ), а струм, що виходить назовні – додатнім ( ).

Від закону збереження заряду у інтегральній формі за допомогою теореми Остроградського-Гаусса можна легко перейти до формулювання закону у диференціальній формі:

.

Диференціальну форму закону збереження заряду можна легко інтерпретувати, використовуючи уявлення про векторні лінії. Якщо в певній точці простору густина заряду з плином часу зменшується, тобто , то ця точка є точкою витоку ліній вектора , оскільки при цьому . Якщо , то , а отже, густина заряду у точці зменшується і вона є точкою стоку.

Якщо початковий розподіл заряду в певній області зберігається (ρ не залежить від часу), то згідно із твердженням потік струму у точках області сталий, або струм в області відсутній.