1.3. Поля та операції векторного аналізу.

У рамках курсу “Векторний аналіз” визначено спеціальні операції диференціювання та інтегрування функцій, які характеризують поля – операції гадієнта (grad), дивергенції (div), ротора (rot), потоку поля, циркуляції поля. Результати таких операцій дозволяють дослідити властивості полів.

Розрізняють поля скалярні та векторні. Відповідно вони моделюються скалярними чи векторними функціями просторових координат та часу.

Скалярне поле описується функцією виду φ . Скалярні поля можна наглядно відобразити за допомогою поверхонь однакового рівня:

φ(x,y,z)=c, c=const.

Схематично такі поверхні показано на рис. 2.

В изначимо вектор, який позначається і який спрямовано у бік максимального зростання функції φ. Абсолютне значення цього вектора визначає швидкість зміни функції φ. Формалізований вид операції градієнта наступний:

,

ν – лінія, ортогональна до поверхні однакового рівня, – одиничний вектор-орт, дотичний до лінії ν.

Зміст операції градієнта ілюструє рис. 3. На малюнку показано елементи двох нескінченно близьких поверхонь однакового рівня та вектор градієнта .

Розрахуємо проекцію вектора на напрямок . Для цього скористаємось співвідношенням:

,

д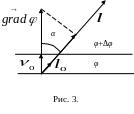 е – одиничний орт, який відповідає напрямку .

Відмітимо, що проекція стає максимальною при куті α=0, тобто коли співпадає з напрямком максимального зростання значення функції φ.

Очевидно, що запропоноване співвідношення можна застосовувати для визначення компонент вектора градієнта у довільній системі відліку. Наприклад, у декартовій системі компоненти вектора будуть наступними:

де – оператор, який визначається правилом: .

Очевидно, що скалярне поле породжує векторне поле:

.

Таке векторне поле називають потенціальним, а функція φ називається потенціалом. Поверхні однакового рівня називають еквіпотенціальними поверхнями.

Для наглядного відображення векторних полів будують так звані силові або векторні лінії. Це лінії, дотична до яких в кожній точці вказує напрямок векторного поля. Кількість ліній, що проходять через одиничну поверхню, пропорційна абсолютному значенню вектора .

Введемо поняття векторного диференціалу вздовж деякої лінії l, цей вектор спрямований по дотичній до лінії l і по абсолютному значенню дорівнює диференціалу dl. Цей вектор у декартовій системі координат можна подати так:

д е – вектор, який спрямовано по дотичній. Векторний диференціал ілюструє рис. 4.

Нехай задано деяке векторне поле , яке потрібно подати у вигляді векторних ліній. Подамо векторну функцію у декартовій системі координат:

Вимагаємо виконання умови: , де k – коефіцієнт пропорційності (k можна подати у вигляді диференціалу dt).

Іншими словами, визначимо коефіцієнт розтягу (стриску) k вектора , щоб він співпадав з диференціалом . Прирівнюючи компоненти вектора і , отримаємо систему диференціальних рівнянь:

,

інтегрування якої дозволяє побудувати рівняння силових ліній.

Розглянемо декілька характерних типів картин силових ліній, які можуть зустрічатися при дослідженні векторного поля в деякій області V, що обмежена поверхнею S.

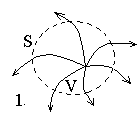
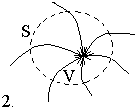
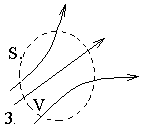
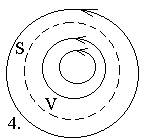
Рис.5.

Рис. 5.1 містить точку, з якої виходять силові лінії. Це точка витоку. Рис. 5.2 містить точку стоку, в яку входять силові лінії. Третій та четвертий малюнки не містять точок витоку або стоку.

У векторному аналізі визначено операції, які дозволяють встановити характер силових ліній поля. Попередньо введемо поняття потоку вектора через поверхню S. Формальне означення потоку Ф має наступний вид:

.

В ектор розглядається як добуток звичайного диференціалу ds на орт нормалі до поверхні s: . Орт вибирається так, щоб він визначав зовнішню нормаль поверхні. Очевидно:

.

Розрахунок потоку поля ілюструє рис.6.

Можна провести аналогію між поняттям потоку поля і потоку речовини, що за одиницю часу проходить через поверхню, яка перпендикулярна напряму потоку.

В тому випадку, коли S – замкнена поверхня, потік визначається інтегралом:

.

Потік є додатнім коли силові лінії виходять з поверхні S назовні, в іншому випадку – від’ємний.

У загальному випадку потік можна оцінити числом силових ліній, які виходять із поверхні. Дійсно, елементарний потік можна розрахувати наступним чином:

.

З іншого боку, величину можна вважати пропорційною числу силових ліній, які пронизують елемент поверхні:

.

Очевидно, що і після інтегрування по поверхні S маємо: .

Повернемося до розгляду малюнків, які ілюструють різні випадки проходження силових ліній через замкнену поверхню S (рис.5). Очевидно, що у першому випадку Ф>0; у другому – Ф<0; у третьому і четвертому – Ф=0.

Дивергенцією вектора називають скалярну величину, яка визначається граничним співвідношенням виду:

.

Дивергенція векторної функції розраховується в точці, околом якої є об’єм ΔV. S – поверхня, яка охоплює об’єм ΔV.

Дивергенцію можна, також, подати у вигляді:

.

Якщо точка, в якій шукається дивергенція є витоком, то очевидно, що якщо точка є стоком, то якщо точка не є стоком або витоком, то .

Операція дивергенції дозволяє характеризувати точки простору на наявність у них джерел поля. Це твердження можна проілюструвати схемами (рис. 7, 8).

Р озглянемо рис.7. При стиску поверхні S у точку P кількість силових ліній, які пронизують поверхню не зміниться. Причому у цій точці . Точка Р у цьому випадку є витоком.

Я кщо точка простору (наприклад М на рис. 8) не є джерелом поля (витоком або стоком), то при стиску поверхні у цю точку кількість силових ліній, що її пронизують починаючи з деякого моменту дорівнює нулю (кількість ліній, які входять у поверхню S дорівнює кількості ліній, що виходять з цієї поверхні). Очевидно, що у точці М .

Використовуючи означення дивергенції можна показати, що в декартовій системі координат ця операція визначається співвідношенням:

Використавши оператор набла ( ), операцію дивергенції можна подати у наступному вигляді

.

Ротором поля називається векторна величина, яка визначена наступним правилом:

.

де ν – напрямок нормалі до поверхні ΔS, яку охоплює контур L, причому вектор ν орієнтовано так, що якщо дивитись в напрямку цього вектора, то напрямок обходу контура L буде відповідати напрямку руху годинникової стрілки (діє правило свердлика, див.рис. 9).

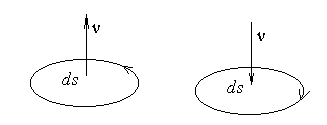
Рис. 9.

Інтеграл по замкненому контуру L у означенні операції ротора називається циркуляцією вектора по контуру L. – вектор-диференціал,

Операція ротора характеризує поле у точці простору. Величина і напрямок ротора визначає величину замкненого потоку поля навколо даної точки (ротор характерихує вихор поля) та його напрямок.

Беручи за основу означення ротора шляхом нескладних перетворень можна розрахувати проекції вектора в декартовій системі координат:

, або:

.

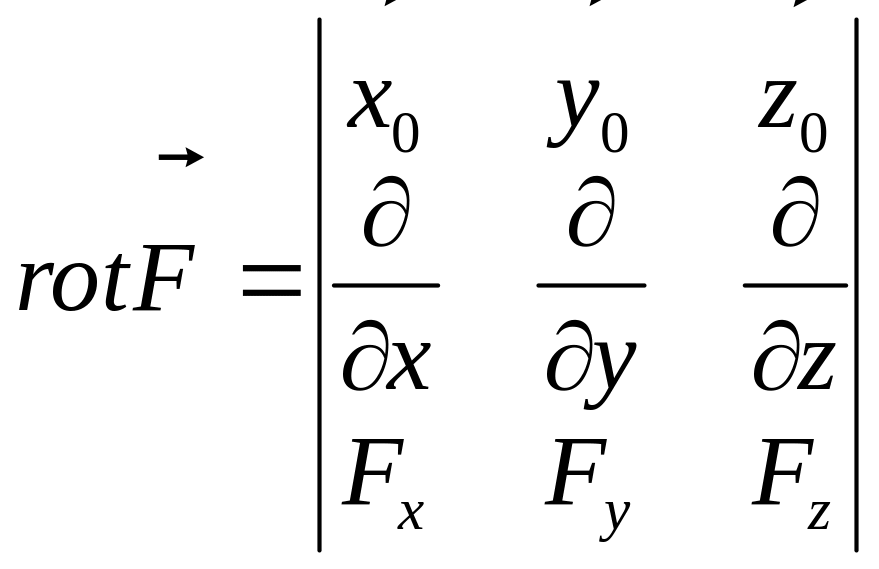Можна переконатись, що для всякого векторного поля, яке отримано за допомогою співвідношення операція =0. Отже, у потенціальних полях вихорів не існує. Такі поля називаються безвихоровими (рис. 5.1, 5.2, 5.3). Поля, для яких (рис. 5.3, 5.4) називаються соленоїдальними. Легко переконатись в тому що , де – деяке векторне поле. Отже, соленоїдальними є векторні поля виду .

Приведемо без доведення деякі твердження векторного аналізу, які використовуються у теорії електромагнетизму

;

Окремо розглянемо перетворення:

,

де – оператор Лапласа.

Оператор набла широко використовується для запису операцій векторного аналізу, зокрема: