§1. Вихідні поняття та рівняння теорії електромагнетизму.

1.1. Математичний апарат теорії поля.

Мовою предмету, який розглядає кількісні величини, традиційно є математичний апарат. Основу математичного апарату теорії електромагнетизму складають методи векторної алгебри і векторного аналізу.

У останні десятиліття поряд із аналітичними методами аналізу широко використовуються чисельні методи. Це обумовлено і зростанням можливостей засобів обчислювальної техніки (з’явились системи автоматизованого проектування), і зростанням складності проблем (відбувся перехід від розгляду простих електродинамічних систем до розгляду складних систем). Застосування ЕОМ для моделювання характеристик електродинамічних пристроїв дозволяє значно скоротити термін розробки систем і здешевити проект.

Поняття вектора як величини відповідає багатьом явищам фізичної реальності. Ця величина крім конкретного значення характеризується напрямком (скалярні величини визначаються лише значеннями). Векторними величинами є, наприклад, сили.

Будь-яку векторну величину можна подати у вигляді:

,

де – одиничний орт, який визначає орієнтацію у просторі; – абсолютне значення вектора .

Орти, які відповідають напрямкам декартової системи координат, позначають відповідно . Тоді будь-який вектор у декартовій системі відліку можна подати наступним чином:

,

– скалярні величини, які є проекціями вектора на осі координат, – компоненти вектора.

У векторній алгебрі визначені наступні основні операції:

1. додавання векторів;

2. скалярний добуток векторів;

3. векторний добуток;

4. змішаний добуток векторів;

5. подвійний векторний добуток.

Додавання двох векторів зводиться до додавання їх компонент:

.

Скалярний добуток двох векторів визначається правилом:

,

де φ – кут між векторами і . Результатом виконання операції є скалярна величина. Скалярний добуток можна подати у вигляді:

.

Очевидно, що скалярний добуток може дорівнювати нулю при відмінних від нуля і . У цьому випадку вектори ортогональні (φ=90°).

Векторний добуток визначається наступними співвідношенням:

.

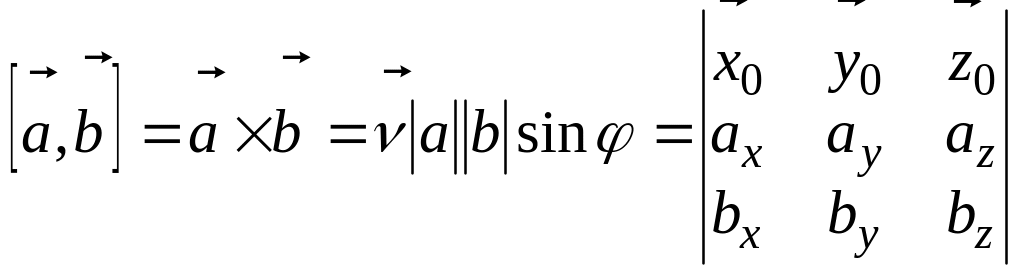Р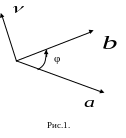 езультатом векторного добутку є вектор орієнтований перпендикулярно до площини, в якій лежать і . Орієнтація результуючого вектора вибирається такою, щоб вектори , і утворювали праву трійку векторів (рис. 1).

Зміна порядку слідування векторів і приводить до зміни знаку перед векторним добутком: .

Для трьох векторів , і визначено добуток, який називається змішаним або векторно-скалярним. Ця операція визначається правилом:

.

Результатом виконання операції є скаляр, який обчислюється розкрттям визначника:

.

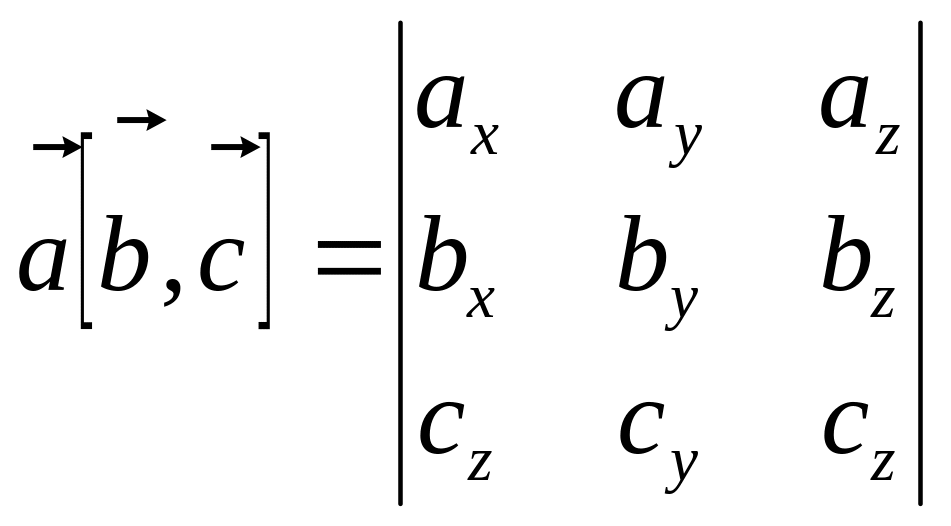Подвійний векторний добуток – це операція, яка визначає вектор за правилом:

.

1.2. Лінійні перетворення, які використовуються у теорії поля.

Результатом множення вектора на скаляр m є вектор , скалярна величина якого визначається правилом: . Визначене співвідношення можна подати у вигляді рівносильної системи рівнянь:

.

Якщо число m додатнє, то вектори і спрямовані однаково (орти векторів однакові), якщо m – від’ємне, то вектори спрямовані у протилежних напрямках. В таких випадках говорить, що і колінеарні.

Вище розглянунуто лише частковий випадок перетворення компонент векторів. У загальному випадку під лінійними перетвореннями розуміють співставлення вектору такого вектора , компоненти якого визначаються співвідношеннями:

.

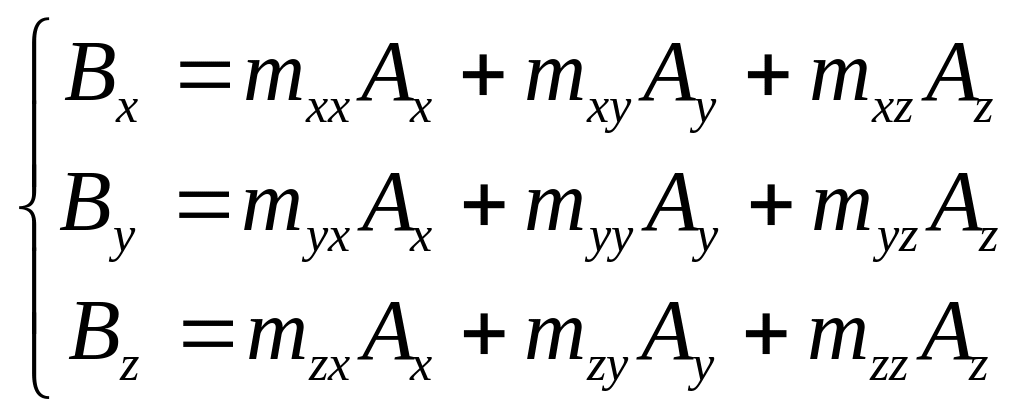Вектори і в загальному випадку не будуть колінеарними. Приведене перетворення векторів визначає поворот одного вектора відносно іншого. З точки зору лінійної алгебри таблиця чисел ,… є матрицею. Записане вище перетворення визначає правило множення матриці на вектор . Таке перетворення можна записати у компактному вигляді: