8.4. Плоскі гармонічні електромагнітні хвилі. Загальний розв’язок хвильового рівняння.

Конкретизуючи вигляд функції φ за умови, що вона описує гармонічні коливання, приходимо до уявлень про гармонічні хвилі:

.

Параметр називають хвильовим числом, швидкість v – фазовою швидкістю. Процес гармонічних коливань ілюструє рис. 24.

Д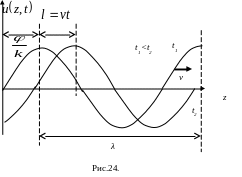 ля будь-яких фіксованих моментів часу t₁, t₂ просторовий розподіл функції є синусоїдальний. Періодом просторових коливань λ є такий приріст координати z, при якому фаза змінюється на значення 2π. Величину λ називають довжиною хвилі. Очевидно, що . Звідки:

.

Таким чином, хвильовий процес повністю характеризується величинами: – амплітудою коливань; ω – частотою коливань (характеризує швидкість часових змін процесу); k – хвильовим числом (характеризує швидкість просторових змін процесу); φ – початковою фазою коливань.

Поширення хвиль можна ілюструвати зміщенням синусоїди вздовж осі z із швидкістю v (рис. 24).

Скористаємось методом комплексних амплітуд для опису гармонічних хвиль, отримуємо:

де – комплексна амплітуда.

В загальному випадку хвильове число k може бути комплексним. Подамо його у наступному вигляді:

.

Підставимо значення комплексної величини k у функцію, що описує гармонічні хвилі. Після виділення дійсної частини комплексної функції отримуємо:

Очевидно, що при функція описує процес згасання хвиль. Амплітуда такої хвилі прямує до нуля при z, що прямує до нескінченності.

Функція є розв’язком хвильового рівняння . У цьому можна переконатись безпосередньою підстановкою.

Очевидно, що загальний розв’язок хвильових рівнянь відносно векторів напруженості поля та можна подати у вигляді:

,

,

де ( , ), ( , ) - амплітуди хвиль, що поширюються відповідно вздовж та проти напрямку вектора . У даному випадку амплітуди є невизначеними векторними константами. Отримано функції, що описують поведінку векторних плоских електромагнітних хвиль.

У декартовій системі відліку вектори , , , , , мають наступні компоненти:

,

,

(вектори , , мають аналогічні компоненти).

Проаналізуємо процес поширення електромагнітних хвиль у необмеженій області. Функція повинна задовольняти третє рівняння Максвелла:

.

Після підстановки функції в явному вигляді у рівняння Максвелла, отримуємо рівність

,

яка повинна виконуватись при довільних значеннях векторів та . Звідси випливає тотожність

,

що відображає факт ортогональності хвилевого вектора , який визначає напрямок поширення хвилі, і вектора напруженості електричного поля.

Для визначення компонент вектора скористаємось другим рівнянням Максвелла:

.

Остаточно маємо: .

Останнє співвідношення є відображенням того, що вектори та перпендикулярні між собою і перпендикулярні напрямку поширення хвилі:

, , .

Говорять, що електромагнітна хвиля є поперечною. Взаємне розміщення векторів , та показано на рис. 25.