§7. Диференціальні рівняння теорії електромагнетизму другого порядку.

7.1. Рівняння Даламбера. Хвильове рівняння.

Для визначення компонент електромагнітного поля в просторі у довільний момент часу потрібно розв’язати систему рівнянь Максвелла, тобто потрібно знайти шість скалярних функцій, які визначають компоненти векторів .

Систему рівнянь Максвелла можна привести до одного диференціального рівняння другого порядку відносно вектора або відносно вектора . Результуюча задача зводиться до визначення уже трьох скалярних функцій.

Застосуємо операцію rot до другого рівняння Максвелла і скористаємось матеріальним рівнянням :

,

де μ – абсолютна магнітна проникність (скалярна функція координат і часу ). Як визначалось вище (п.4.1), абсолютна магнітна проникність визначається добутком: , де μ_в – відносна магнітні проникність (величина, що характеризує реакцію матеріального середовища на дію зовнішнього поля).

Подамо у наступному вигляді:

.

Останню рівність використаємо для перетворення першого рівняння Максвелла до виду:

.

Подальші викладки суттєво спростить припущення про те, що середовище має недисперсійні властивості (функції абсолютної електричної проникності ε та абсолютної магнітної проникності μ не залежать від часу і є функціями координат: , ). Таким чином, друге рівняння Максвелла можна записати так:

,

або

.

Результуюче рівняння – це диференціальне рівняння в частинних похідних другого порядку відносно вектора . Аналогічним способом отримують рівняння для розрахунку компонент вектора .

Це рівняння можна суттєво спростити, припустивши, що матеріальне середовище однорідне ( , або ). В цьому випадку і рівняння набуває наступного вигляду:

.

Остаточний результат отримуємо після застосування третього рівняння Максвелла:

.

Аналогічне рівняння можна записати для вектора :

.

Знайдені рівняння називають векторними рівняннями Даламбера. Відмітимо загальну особливість рівнянь Даламбера: у правій частині рівності містяться доданки, які визначають розподіл зарядів і струмів у середовищі, а у лівій частині – доданки, які визначають створені зарядами і струмами поле. Якщо у середовищі відсутні заряди та струми, то рівняння, очевидно, стають однорідними:

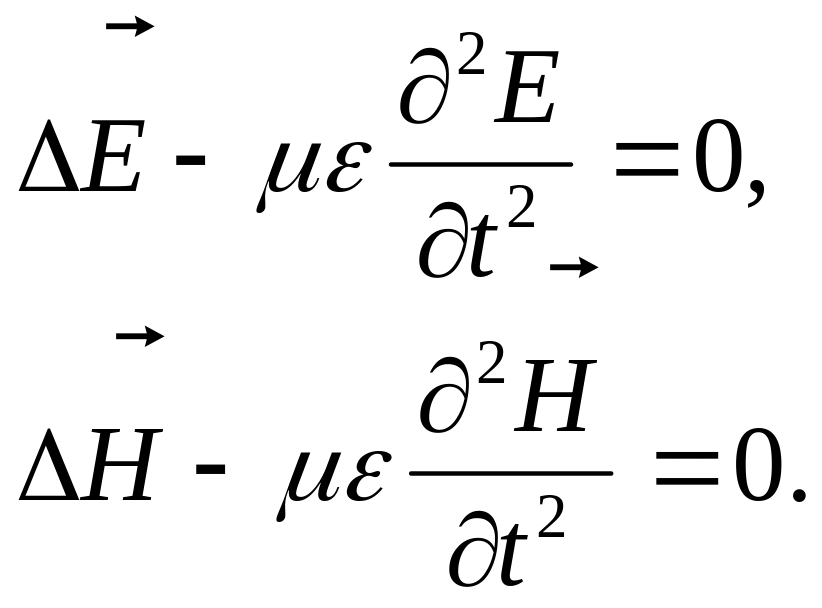
Отримані рівняння називаються хвильовими рівняннями.

7.2. Електромагнітні потенціали.

Для аналізу багатьох електродинамічних задач ефективно використо-вується метод потенціалу. Суть методу полягає у тому, що вводиться деяка допоміжна скалярна або векторна функції, які називаються електро-магнітними потенціалами і через які визначають компоненти векторів електромагнітного поля.

Розглянемо основні ідеї методу. У основу розгляду покладемо четверте рівняння Максвелла:

.

Рівняння вказує на те, що можна побудувати деяку функцію , яка буде визначати магнітне поле наступним чином:

.

Очевидно, що .

Введену таким чином функцію називають векторним потенціалом.

Підставимо вираз у друге рівняння Максвелла ( ), отримаємо:

.

Дана рівність буде виконуватись завжди, якщо покласти (оскільки ). Введену у такий спосіб функцію φ називають скалярним потенціалом, або просто потенціалом. Очевидно, що будь-яке електромагнітне поле можна описати функціями і .

Отримаємо диференціальні рівняння другого порядку відносно функцій і . Для цього вирази для функцій через потенціали та матеріальні рівняння підставимо у перше і третє рівняння Максвелла. Перше рівняння набуває вигляду:

, або

.

Перепишемо третє рівняння Максвелла:

, або

.

Таким чином, у результаті перетворень отримали рівняння Даламбера відносно електромагнітних потенціалів.

Векторний потенціал та скалярний потенціал визначенні неоднозначно. Очевидно, що рівність не порушується після заміни функції сумою . Підставимо суму у вираз для визначення , отримаємо

,

де .

Безпосередньою підстановкою можна переконатися, що функції та задовольняють рівнянню Даламбера відносно векторного та скалярного потенціалів.

Неоднозначність визначення векторного потенціалу та скалярного потенціалу , дозволяє накласти на рівняння Даламбера такі додаткові умови, які спрощують ці рівняння. Додаткова умова визначена наступним чином:

.

Вона отримала назву – умова калібрування Лоренца.

Умова калібрування дозволяє привести рівняння Даламбера відносно векторного потенціалу до вигляду:

.

Врахуємо тотожність і в результаті отримуємо хвильове рівняння відносно функції :

.

Аналогічним способом можна отримати рівняння Даламбера відносно функції :

.