6.3. Енергія електромагнітного поля.

Розглянемо рівняння балансу енергії для консервативної системи:

.

Перетворимо підінтегральний вираз. При цьому використаємо матеріальні рівняння і умову стаціонарності електромагнітного поля. Отримуємо:

,

.

Очевидно, що: .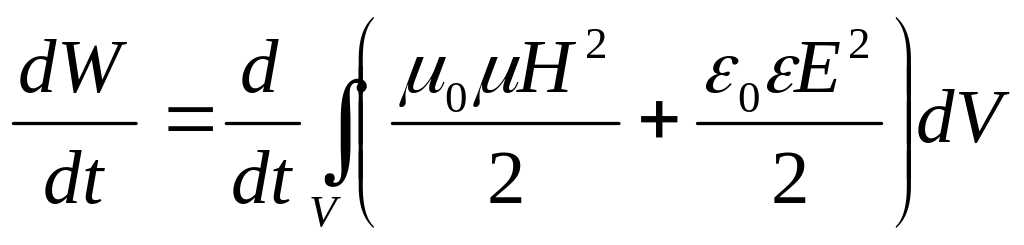

Величину називають енергією електромагнітного поля.

Перший доданок підінтегральної суми визначає густину енергії магнітного поля, а другий – густину енергії електричного поля. Густину енергії можна подати наступним співвідношенням:

.

Вектор Пойтинга можна трактувати як густину потоку енергії. Можна провести аналогію між процесами протікання струму та протікання енергії. Енергетичний аналог потоку струму – потік енергії:

,

де w – густина енергії, v – швидкість потоку енергії.

Отже, якщо в певному середовищі є відомим розподіл поля, то розраховуючи величину енергії і вектор Пойтинга, можна знайти швидкість поширення електромагнітного поля у середовищі.

Рівняння балансу енергії можна записати у диференціальній формі. Для цього потрібно скористатися теоремою Остроградського-Гаусса. В результаті отримаємо:

.

Дане рівняння характеризує локальний баланс енергії. Відмітимо подібність рівняння балансу енергії із законом збереження заряду.

Задачі до §4-6.

1. Для кварцу , , а інші компоненти тензора рівні нулю. При якій орієнтації векторів і вони зберігають паралельність?

2. Чому волога земля веде себе як провідник, або як діелектрик? Вказати відповідні умови.

3. Показати, що вектор напруженості електричного поля завжди перпендикулярний до поверхні ідеального провідника, а вектор індукції магнітного поля завжди пералельний поверхні ідеального провідника.

Розв’язання:

Р озглянемо елемент поверхні розділу непровідного середовища (1) і ідеального провідника (2). Нехай у середовищі 1 існує поле, яке не проникає в середовище 2 (у ідеальному провіднику струми провідності компенсують появу будь-якого поля). Таким чином, маємо:

,

.

Використаємо граничні умови для вектора ( ). Оскільки тангенціальна компонента вектора напруженості електричного поля , то з граничних умов випливає, що і . Отже, вектор в середовищі 1 повинен орієнтуватися по нормалі до поверхні ідеального провідника (рис.20).

У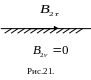 об’ємі середовища 2 вектор індукції магнітного поля . Очевидно, що нормаль до поверхні цього вектора . Використаємо граничні умови для вектора ( ), з яких випливає рівність нулю нормальної компоненти вектора індукції магнітного поля у середовищі 1: . Таким чином, в даній системі буде орієнтований вздовж границі розділу (рис.21).

4. Вивести граничні умови для векторів і на поверхні ідеального провідника.

5. Розглядається багатошарова структура, елементи якої характеризуються діелектричними проникностями . У середовищі із діелектричною проникністю існує електричне поле , силові лінії якого із поверхнею розділу середовищ складають кут α (рис.22.). Знайти значення напруженості і індукції електричного поля в усих шарах структури.

6. Розрахувати потік енергії через поверхню нескінченного циліндричного провідника з постійним струмом І.

7 . Знайти електричну енергію плоского конденсатора.

8. Показати, що запас енергії ізольованої системи змінюється за законом , якщо ця величина пропорційна потужності втрат. Який зміст величини α ?

Контрольні запитання до §4-6.

1. Розкрийте зміст матеріальних рівнянь.

2. Які властивості матеріальних середовищ можуть передавати матеріальні рівняння?

3. Що відображають поняття поляризації та намагнічування?

4. Які матеріали називають провідниками, діелектриками?

5. За яким критерієм проводять розділення речовин на провідники та діелектрики?

6. Визначте граничні умови для векторів індукції та напруженості електричного поля.

7. Визначте граничні умови для векторів індукції та напруженості магнітного поля.

8. Розкрийте зміст рівняння балансу енергії.