5.4. Граничні умови для векторів магнітного поля.

На границі розділу середовищ вектор індукції магнітного поля повинен задовольняти наступні умови:

.

Отже, нормальна компонента вектора на границі розділу неперервна. Для доведення твердження необхідно використати четверте рівняння Максвелла у інтегральній формі. Хід доведення аналогічний тому, який викладено у п.5.2.

Граничні умови для вектора індукції магнітного поля мають наступний вигляд:

,

де – вектор густини поверхневого струму.

Таким чином, тангенціальна компонента вектора напруженості магнітного поля на границі розділу середовищ має розрив. Для доведення сформульованого твердження потрібно скористатись першим рівнянням Максвелла у інтегральній формі. Хід доведення аналогічний тому, який приведено у п.5.3.

§6. Енергетичні співвідношення для електромагнітних полів.

6.1. Закон Джоуля-Ленца.

Електромагнітне поле, як і інші матеріальні об’єкти, має енергію. Встановимо яким чином напруженості полів , та індукції , визначають енергію поля W.

При проходженні електричного струму через провідник на ньому виділяється тепло. Кількість теплоти визначається законом Джоуля-Ленца (закон встановлено експериментально):

,

де ΔQ – кількість виділеної теплоти, I – величина струму, U – напруга на кінцях провідника, Δt – час дії стуму, величину називають потужністю теплових втрат.

Потужність, що виділяється в об’ємі провідника, визначають наступним інтегралом:

,

де – густина потужності втрат. Дійсно, оскільки потужність – це робота, яка виконана за одиницю часу: . І за означенням роботи , де – сила, що діє на заряджені частинки, – переміщення заряджених частинок. Нагадаємо, що . То після виконання нескладних перетворень, отримуємо: .

У залежності від напрямку руху зарядів величина р може бути як додатною, так і від'ємною. Якщо вектори і спрямовані в один бік то , якщо у різні – .

В першому випадку енергія у поля відбирається, в другому випадку енергія передається полю. Це означає, що заряджені частинки рухаються проти дії поля керовані, наприклад, механічною силою. Сторонні сили передають енергію полю, яке гальмує заряд. Дія сторонніх сил у формальному вигляді може бути врахована у матеріальному рівнянні:

.

6.2. Баланс енергії поля.

Запишемо перше і друге рівняння Максвелла, домноживши їх скалярно відповідно на вектор та вектор :

,

.

Віднімаючи від другого рівняння перше, отримуємо:

.

Для встановлення змісту отриманого рівняння приведемо його до інтегральної форми запису. Для цього виконаємо інтегрування по деякому об'єму V, який обмежено поверхнею S:

.

Під час виконання перетворень задіяно теорему Остроградського-Гаусса. Отримане рівняння називають рівнянням балансу енергії в об’ємі V.

Останній доданок у правій частині – потужність. Отже, усі інші елементи рівняння також мають розмірність потужності. Відомо, що для будь-якої ізольованої системи рівняння балансу енергії має вид:

,

де W – енергія системи.

Дане твердження є відображенням того, що витрати енергії ( ) можуть існувати лише в тому випадку, коли , тобто лише за рахунок зменшення запасу енергії системи.

Розглянемо випадок, коли границя області V є енергетично ізольованою. Це означає, що при наявності поля в об’ємі V воно відсутнє за межами границі S. Застосувавши граничні умови для векторів напруженості поля (див. §5), приходимо до висновку, що на поверхні S тангенціальна складова напруженості електричного поля дорівнює нулю: . Таким чином, ліва частина рівняння енергетичного балансу дорівнює нулю. Рівняння енергетичного балансу набуде вигляду.

,

або, з врахуванням визначення потужності,:

.

Рівняння енергетичного балансу у загальному випадку тепер можна подати так:

, або .

Наслідком неізольованості системи є поява у рівнянні поверхневого інтегралу, який є потоком деякого вектора через поверхню S. Вектор називають вектором Пойтинга.

П отік вектора Пойтинга – це величина, яка показує на скільки внутрішні процеси у системі є врівноваженими. Якщо величина потоку додатня, то це свідчить про втрати енергії у системі. І навпаки, якщо потік від’ємний, то це означає, що енергія надходить у систему. Потік вектора Пойтинга – це кількість енергії, яка проходить через поверхню S за одиницю часу. Тобто це є потужність, випромінювання енергії у зовнішній простір, або це є потужність поглинання енергії.

Схематично розглянемо різні випадки балансу енергії у системі (рис. 19). Активний баланс у об’ємі V ілюструють рис. 19 а), б); нейтральний баланс – рис. 19 в), г), д); рис. 19 е), є) – пасивний баланс.

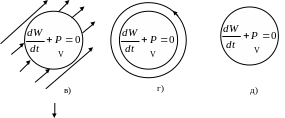
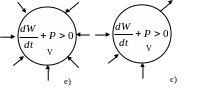
Рис. 19.