Егэ без ошибок. Считаем быстро и без калькулятора

Вы хотите хорошо сдать ЕГЭ по математике? Тогда вам необходимо уметь считать быстро, правильно и без калькулятора. Ведь главная причина потери баллов на ЕГЭ по математике – вычислительные ошибки.

По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике запрещается. Цена может быть слишком высокой — удаление с экзамена.

На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи решаются без него. Главное – внимание, аккуратность и некоторые секретные приемы, о которых мы расскажем.

. Начнем с главного правила. Если какое-то вычисление можно упростить – упростите его.

Вот, например, такое «дьявольское уравнение»:

Семьдесят процентов выпускников решают его «в лоб». Считают дискриминант по формуле , после чего говорят, что корень невозможно извлечь без калькулятора. Но ведь можно разделить левую и правую части уравнения на . Получится

Какой способ проще? :-)

. Многие школьники не любят умножение в «столбик». Никому не нравилось в четвертом классе решать скучные «примеры». Однако перемножить числа во многих случаях можно и без «столбика», в строчку. Это намного быстрее.

Обратите внимание, что мы начинаем не с меньших разрядов, а с бoльших. Это удобно.

. Теперь – деление. Нелегко «в столбик» разделить на . Но вспомним, что знак деления : и дробная черта – одно и то же. Запишем в виде дроби и сократим дробь:

Другой пример.

. Как быстро и без всяких столбиков возвести в квадрат двузначное число? Применяем формулы сокращенного умножения:

Иногда удобно использовать и другую формулу:

. Числа, оканчивающиеся на , в квадрат возводятся моментально.

Допустим, надо найти квадрат числа ( — не обязательно цифра, любое натуральное число). Умножаем на и к результату приписываем . Всё!

Например:   ( и приписали ).

  ( и приписали ).

  ( и приписали ).

Этот способ полезен не только для возведения в квадрат, но для извлечения квадратного корня из чисел, оканчивающихся на .

. А как вообще извлечь квадратный корень без калькулятора? Покажем два способа.

Первый способ – разложение подкоренного выражения на множители.

Например, найдем Число делится на (так как сумма его цифр делится на ). Разложим на множители:

Найдем . Это число делится на . На оно тоже делится. Раскладываем на множители.

Еще пример.

Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.

Например, надо найти . Число под корнем – нечетное, оно не делится на , не делится на , не делится на … Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.

Очевидно, что в квадрат возводили двузначное число, которое находится между числами и , поскольку , , а число находится между ними. Первую цифру в ответе мы уже знаем, это .

Последняя цифра в числе равна . Поскольку ,   , последняя цифра в ответе – либо , либо . Проверим: . Получилось!

Найдем .

,   . Значит, первая цифра в ответе – пятерка.

В числе последняя цифра – девятка. ,   . Значит, последняя цифра в ответе – либо , либо .

Проверим:

Если число, из которого надо извлечь квадратный корень, заканчивается на или – значит, квадратный корень из него будет числом иррациональным. Потому что ни один квадрат целого числа не заканчивается на или . Помните, что в задачах части вариантов ЕГЭ по математике ответ должен быть записан в виде целого числа или конечной десятичной дроби, то есть должен являться рациональным числом.

. Квадратные уравнения встречаются нам в задачах , и вариантов ЕГЭ, а также в части . В них нужно считать дискриминант, а затем извлекать из него корень. И совсем не обязательно искать корни из пятизначных чисел. Во многих случаях дискриминант удается разложить на множители.

Например, в уравнении

. Иногда дискриминант удается посчитать по известной формуле сокращенного умножения: . Вот, например, такое уравнение вполне может получиться при решении задачи :

. Еще одна ситуация, в которой выражение под корнем можно разложить на множители, взята из задачи .

Гипотенуза прямоугольного треугольника равна , один из катетов равен , найти второй катет.

По теореме Пифагора, он равен . Можно долго считать в столбик, но проще применить формулу сокращенного умножения.

А теперь расскажем самое интересное — из-за чего все-таки выпускники теряют на ЕГЭ драгоценные баллы. Ведь ошибки в вычислениях возникают не просто так.

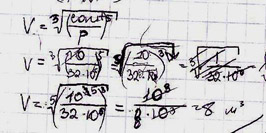1. Верный путь к потере баллов — неаккуратные вычисления, в которых что-то исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите на свои черновики. Возможно, они выглядят так же? :-)

Пишите разборчиво! Не экономьте бумагу. Если что-то неправильно – не исправляйте одну цифру на другую, лучше напишите заново.

2. Почему-то многие школьники, считая в столбик, стараются сделать это 1) очень-очень быстро, 2) очень мелкими цифрами, в уголке тетради и 3) карандашом. В результате получается вот что:

   

Разобрать что-либо невозможно. Что ж тогда удивляться, что оценка за ЕГЭ ниже, чем ожидали?

3. Многие школьники привыкли игнорировать скобки в выражениях. Иногда встречается и такое:

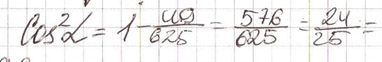Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике.

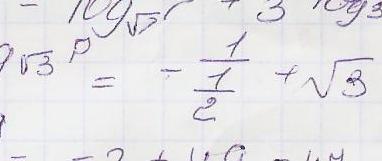4. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что Здесь нарисован «гамбургер», то есть многоэтажная дробь. Крайне сложно при таком способе получить правильный ответ.

Подведем итоги.

Проверка заданий части – автоматическая. Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет. Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому в ваших интересах научиться считать быстро, правильно и без калькулятора.