Радиус описанной окружности
Радиус описанной окружности трапеции по сторонам и диагонали
| Печать |
a - боковые стороны трапеции
c - нижнее основание
b - верхнее основание
d - диогоаналь
h - высота
p - полупериметр, p=(a+b+c)/2
Формула радиуса описанной окружности трапеции, (R)
Радиус описанной окружности правильного многоугольника
| Печать |
a - сторона многоугольника
N - количество сторон многоугольника
Радиус описанной окружности правильного многоугольника, (R):
Радиус описанной окружности правильного шестиугольника
| Печать |
a - сторона шестиугольника
d - диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Радиус описанной окружности прямоугольника по стороне
| Печать |
a, b - стороны прямоугольника
d - диагональ
Радиус описанной окружности прямоугольника (R):
Найти радиус описанной окружности около квадрата
| Печать |
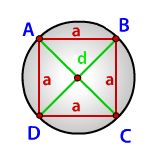
a - сторона квадрата
d - диагональ
Радиус описанной окружности квадрата (R):
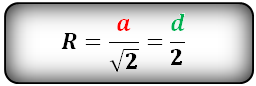
Найти радиус описанной окружности треугольника по сторонам
| Печать |
a, b, c - стороны треугольника
Радиус описанной окружности треугольника, (R):
Найти радиус описанной окружности равностороннего треугольника по стороне
| Печать |
a - сторона треугольника
Радиус описанной окружности равностороннего треугольника (R):
найти радиус описанной окружности равнобедренного треугольника по сторонам
| Печать |
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b - стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
| Печать |
a, b - катеты прямоугольного треугольника
c - гипотенуза
Радиус описанной окружности прямоугольного треугольника (R):
Формулы объема и площади поверхности. Цилиндр, конус и шар
Если в задаче В9 на ЕГЭ по математике вам надо просто посчитать объем конуса или площадь сферы — считайте, что повезло. Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице.
В
некоторых задачах
,
кроме формул, нужна еще и элементарная
логика. Например, если линейные размеры
тела вращения уменьшились в два раза —
его площадь поверхности уменьшится в
,
а объем — в
раз
(ведь
,
).
Как, например, в этой задаче. Как и
остальные, она взята из банка заданий
ФИПИ.
1.
Объем конуса равен
.
Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Очевидно,
что объем меньшего конуса в
раз
меньше объема большого и равен двум.
Для
решения некоторых задач полезны хотя
бы начальные знания стереометрии.
Например — что такое правильная пирамида
или прямая призма. Полезно помнить, что
у цилиндра, конуса и шара есть еще общее
название — тела вращения. Что сферой
называется поверхность шара. А, например,
фраза «образующая конуса наклонена к
плоскости основания под углом
?»
предполагает, что вы знаете, что такое
угол между прямой и плоскостью. Вам
также может пригодиться теорема Пифагора
и простые формулы
площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2.
Во сколько раз объем конуса, описанного
около правильной четырехугольной
пирамиды, больше объема конуса, вписанного
в эту пирамиду?
Всё
просто — рисуем вид снизу. Видим, что
радиус большего круга в
раз
больше, чем радиус меньшего. Высоты у
обоих конусов одинаковы. Следовательно,
объем большего конуса будет в
раза
больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или ? у вас в ответе в части В быть не должно. Подставлять приближенное значение ? тоже не нужно! Помните, что оно обязательно должно сократиться. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ?».