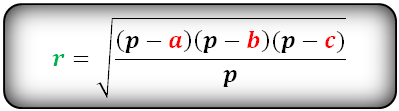- •3. Теперь рассмотрим знаки подмодульных выражений на каждом промежутке:
- •4. Решим уравнение на каждом промежутке:
- •5. Теперь объединим полученные решения, и запишем ответ:
- •Радиус вписанной окружности
- •Радиус описанной окружности
- •Формулы объема и площади поверхности. Цилиндр, конус и шар
- •Формулы объёма и площади поверхности. Всё для решения задач в9 и в11
- •Задачи по стереометрии в9 и в11 Часть 1: Просто применяем формулы
- •Задачи по стереометрии в9 и в11. Часть 2: Приемы и секреты
- •Егэ без ошибок. Считаем быстро и без калькулятора
- •Площадь поверхности объемных тел
Название метода мажорант происходит от французских слов majorer - объявлять большим и minorer – объявлять меньшим.
Метод мажорант основан на том, что множество значений некоторых функций ограничено. При использовании метода мажорант мы выявляем точки ограниченности функции, то есть в каких пределах изменяется данная функция, а затем используем эту информацию для решения уравнения или неравенства.
Чтобы успешно пользоваться этим методом, нужно хорошо знать, какие функции имеют ограниченное множество значений.
Приведем примеры элементарных функций, которые имеют ограниченное множество значений:
1.
![]()
![]() или
или ![]()
2.
![]() или
или ![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
Маркером того, что в данном уравнении нужно применить метод мажорант, является
a) наличие в уравнении функций, уравнения с которыми решаются принципиально разными способами. Например, если в одной части уравнения стоит многочлен, а в другой – тригонометрические функции.
б) или если очевидно, что стандартными методами уравнение не решить.
При решении уравнения с помощью метода мажорант , мы, как правило:
выясняем, что правая часть уравнения больше или равна какого-то числа, а левая – меньше или равна. Или наоборот.
равенство возможно, если обе части уравнения равны этому числу
приравниваем ту часть уравнения, которая проще, к этому числу и находим соответствующее значение х
проверяем, что при этом значении х другая часть уравнения также равна этому числу.
Рассмотрим примеры уравнений такого рода:
1.
Решите уравнение:
![]()
Очевидно, что мы не будем возводить двучлен в четвертую степень и трехчлен в десятую.
Заметим, что 4 и 10 – четные числа, следовательно,
![]() при
любом значении х
при
любом значении х
и
![]() при
любом значении х.
при
любом значении х.
Равенство
возможно, если одновременно ![]() и
и ![]()
Корень
первого уравнения ![]() ,
,
корни
второго уравнения ![]() и
.
Число
является корнем обоих уравнений, его
мы и запишем в ответ.
и
.
Число
является корнем обоих уравнений, его
мы и запишем в ответ.
Ответ: 3
2. Решите неравенство:
![]()
1. Упростим первый корень:
![]()
2. Не будем торопиться раскрывать модуль. Заметим, что оба слагаемых в левой части неравенства неотрицательны, следовательно, правая часть также должна быть неотрицательна, то есть
![]()
![]()
При
этих значениях ![]() подмодульное выражение отрицательно,
следовательно, раскрываем модуль с
противоположным знаком:
подмодульное выражение отрицательно,
следовательно, раскрываем модуль с
противоположным знаком:
![]()
![]()
В
правой и левой частях неравенства
стоит выражение ![]() .
Вычтем его из обеих частей неравенства:
.
Вычтем его из обеих частей неравенства:
![]()
Так как квадратный корень – величина неотрицательная, следовательно, неравенство выполняется только если левая часть равна нулю.
3. Остается решить уравнение
![]()
а) Приведем второй логарифм к основанию 2:
![]()
б) Преобразуем первое слагаемое:
![]() –
мы
раскрыли модуль с тем же знаком, так
как
–
мы
раскрыли модуль с тем же знаком, так
как ![]() по ОДЗ исходного неравенства.
по ОДЗ исходного неравенства.
в)
Теперь мы можем ввести замену переменной: ![]() .
.
Получим
уравнение:![]()
Отсюда ![]() или
или
![]()
в) Вернемся к исходной переменной:
![]() или
или
![]()
Отсюда ![]() или
или
![]()
Легко проверить что оба числа являются решениями исходного неравенства. Так как мы не находили ОДЗ, проверку сделать необходимо.
Ответ:
1; ![]()
3.
a) Решите
уравнение:
![]()
б)
Найдите
все корни уравнения, на промежутке ![]()
1. Оценим, в каких пределах может принимать значения левая часть неравенства:
![]()
![]()
![]()
Так как все части неравенства положительны, прологарифмируем неравенство:
![]()
![]()
Итак, левая часть неравенства больше или равны единицы.
2. Оценим, в каких пределах может принимать значения правая часть неравенства:
![]()
Получили, что правая часть неравенства меньше или равна единицы.
Равенство возможно, только если обе части одновременно равны 1.
Найдем при каких значениях выполняется равенство
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Итак, левая часть уравнения равна 1 при
![]()
Найдем при каких значениях х правая часть равна 1.
![]() если
если
![]()
![]()
![]()
![]()
![]()
Итак, правая часть уравнения равна 1 при
Это решение должно совпадать с тем значением , при котором левая часть равна 1.
Выпишем
значения
из промежутка ![]() :
:
При ![]()
![]()
При ![]()
![]()
При ![]()
![]()
При
![]()
![]()
При
![]()
![]() – эта точка совпадет с первой точкой и
цикл начнется снова.
– эта точка совпадет с первой точкой и
цикл начнется снова.
Вспомним,
что левая часть уравнения равна 1
при ![]()
Выпишем значения из промежутка
При ![]()
![]()
При ![]()
![]()
При ![]()
![]()
При ![]()
![]() – эта точка совпадает с первой точкой,
и цикл начинается снова.
– эта точка совпадает с первой точкой,
и цикл начинается снова.
Мы
видим, что при ![]() обе части уравнения равны 1.
обе части уравнения равны 1.
Итак,
решение
уравнения ![]()
Ответим на вторую часть задания:
б)
Найдите все корни уравнения на промежутке ![]()
Отметим
на тригонометрическом круге полученное
решение – эта точка изображена фиолетовым
цветом. Она отстоит от
![]() на
на
![]()
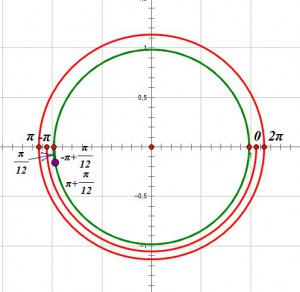
Мы
начинаем движение по кругу из точки
![]() ,
и первое решение, которое нам встречается
соответствует углу поворота на
,
и первое решение, которое нам встречается
соответствует углу поворота на
![]()
Затем
мы проходим по кругу точку 0, точку
![]() и
следующее решение, которое принадлежит
указанному промежутку
и
следующее решение, которое принадлежит
указанному промежутку
![]()
Ответ: а)
б)
![]() ,
,
![]()
В этой статье я расскажу, как решать тригонометрические уравнения с помощью разложения на множители. Чаще всего разложение на множители применяется в уравнениях, которые содержат тригонометрические функции с углами, кратность которых больше трех.
При решении тригонометрических уравнений с помощью разложения на множители мы преобразуем сумму или разность тригонометрических функций в произведение с помощью тригонометрических формул:
![]()
![]()
![]()
![]()
Заметим, что во всех этих формулах присутствует полусумма и полуразность аргументов синуса и косинуса.
Алгоритм применения метода разложения на множители я покажу на таком классическом уравнении:
![]()
1. Наша задача сгруппировать синусы по два так, чтобы при разложении на множители в каждой группе появилсь однаковые множители.
Попробуем сгруппировать так:
![]()
2. Сумму синусов в каждой скобке разложим на множители:
![]()
Упростим, и учтем четность косинуса:
![]()
Удалось!
В каждом произведении у нас есть
одинаковый множитель ![]()
(Если общий множитель не появился, нужно попробовать сгруппировать по-другому. )
3.
Вынесем общий множитель ![]() за скобку:
за скобку:
![]()
4. Еще раз преобразуем в произведение сумму синусов в скобках:

![]()
5. Так как каждый множитель произведения не имеет ограничений на ОДЗ, просто приравняем каждый множитель к нулю:
a)
![]() ,
,
![]() ,
,
![]()
![]() ,
,
б) ![]()
![]() ,
,
![]()
![]() ,
,
в)
![]()
![]() ,
,
![]()
Ответ: , ,
,
,
Иногда, прежде чем преобразовывать сумму тригонометрических функций в произведение, нужно сначала преобразовать произведение в сумму.
Для этого мы используем вот эти тригонометрические формулы:
![]()
![]()
![]()
Решим уравнение:
![]()
Уравнение в таком виде нам не удается разложить на множители. Преобразуем сначала произведения в правой и левой части уравнения в сумму:
![]()
![]()
Получим:
![]()
![]()
![]()
Преобразуем разность синусов в произведение:
![]()
![]()
![]()
Приравняем каждый множитель к нулю:
![]() ,
, ![]()
![]()
![]() ,
, ![]()
Ответ: ,
И, наконец, предлагаю вам посмотреть ВИДЕОУРОК с подробным решением тригонометрического уравнения из Задания С1:
Решить
уравнение
![]() ,
в ответе записать решения уравнения,
принадлежащие промежутку
,
в ответе записать решения уравнения,
принадлежащие промежутку ![]()
В этой статье я покажу алгоритм решения уравнений, которые содержат несколько выражений под знаком модуля, на примере решения уравнения уровня С1, а затем вы посмотрите ВИДЕУРОК с подробным разбором тригонометрического уравнения с модулем уровня С3.
Давайте решим уравнение:
![]()
Вспомним, что модуль раскрывается по такому правилу:
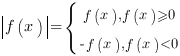
Говоря человеческим языком, модуль выражения равен самому выражению, если оно неотрицательно, и выражению с противоположным знаком, если оно меньше нуля.
Таким образом, перед нами стоит задача раскрыть все модули в соответствии со знаками подмодульных выражений.
Будем следовать такому алгоритму:
1. Определим, в каких точках каждое подмодульное выражение меняет знак. Для этого приравняем каждое подмодульное выражение к нулю:
![]() ,
, ![]()
![]()
![]() ,
, ![]()
Мы получили три точки.
2. Нанесем их на числовую ось:

Эти три числа разбили числовую ось на четыре промежутка:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Обратите внимание, что мы включили крайние точки промежутков в оба промежутка. Ничего страшного не случится, если мы эти точки учтем два раза, главное, о них не забыть.
3. Теперь рассмотрим знаки подмодульных выражений на каждом промежутке:
Выражение
![]() меняет
знак в точке
.
Слева от этой точки оно отрицательно,
а справа положительно. Отметим это в
таблице:
меняет
знак в точке
.
Слева от этой точки оно отрицательно,
а справа положительно. Отметим это в
таблице:

Выражение меняет знак в точке . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:
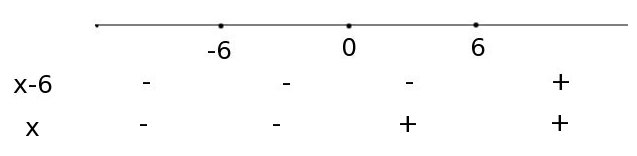
Выражение
![]() меняет
знак в точке
.
Слева от этой точки оно отрицательно,
а справа положительно. Отметим это в
таблице:
меняет
знак в точке
.
Слева от этой точки оно отрицательно,
а справа положительно. Отметим это в
таблице:
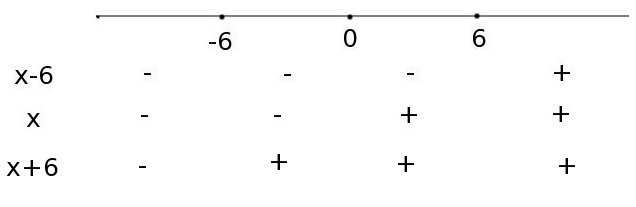 Мы
получили знаки всех подмодульных
выражений на каждом промежутке. Теперь
раскроем модули на каждом промежутке
с учетом этих знаков.
Мы
получили знаки всех подмодульных
выражений на каждом промежутке. Теперь
раскроем модули на каждом промежутке
с учетом этих знаков.
Наше уравнение «распадается» на четыре уравнения по количеству числовых промежутков.
4. Решим уравнение на каждом промежутке:
1. 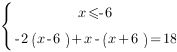
![]()
![]()
![]()
Решение уравнения на первом промежутке
2.Раскроем модули на втором промежутке:
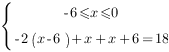
![]()
![]()
Мы получили, что второе уравнение системы является тождеством, то есть второе равенство верно при любом действительном значении . Следовательно, решением системы будут те значения неизвестного, которые удовлетворяют первому неравеству:
![]() .
.
3. Раскроем модули на третьем промежутке:
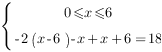
![]()
![]()
![]()
Решение уравнения на третьем промежутке:
4. Раскроем модули на четвертом промежутке:
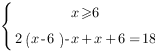
![]()
Заметим, что решения нашего уравнения на каждом промежутке принадлежали этому промежутку, то есть удовлетворяли неравенству каждой системы. Однако, так бывает не всегда, и если корень уравнения не удовлетворяет неравенству, значит, соответствующая система не имеет решений.
5. Теперь объединим полученные решения, и запишем ответ:
Ответ: -6≤х≤0, х=12
Радиус вписанной окружности
![]()
Радиус вписанной окружности в шестиугольник
| Печать |
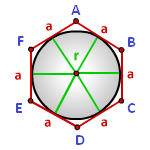
a - сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
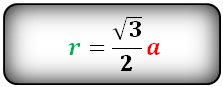
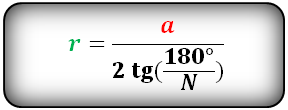
Радиус вписанной окружности в правильный многоугольник
| Печать |
a - сторона многоугольника
N - количество сторон многоугольника
Радиус вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в ромб
| Печать |
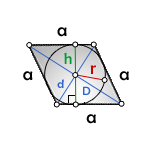
r - радиус вписанной окружности
a - сторона ромба
D, d - диагонали
h - высота ромба
Формула радиуса вписанной окружности в ромб, (r):
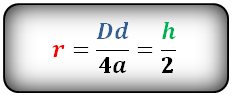
Радиус вписанной окружности в квадрат
| Печать |
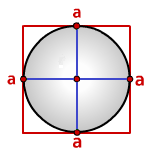
a - сторона квадрата
Радиус вписанной окружности в квадрат (r):
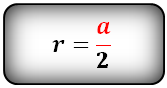
Радиус вписанной окружности в равнобочную трапецию
| Печать |
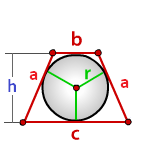 с
-
нижнее основание
с
-
нижнее основание
b - верхнее основание
a - боковые стороны
h - высота
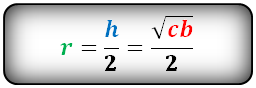
Радиус вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в прямоугольный треугольник
| Печать |
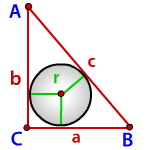
a, b - катеты треугольника
с - гипотенуза
Радиус вписанной окружности в прямоугольный треугольник (r):
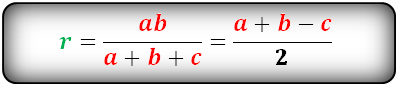
Радиус вписанной окружности в равнобедренный треугольник
| Печать |
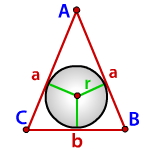
a, b - стороны треугольника
Радиус вписанной окружности в равнобедренный треугольник (r):
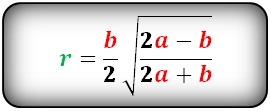
Радиус вписанной окружности в равносторонний треугольник
| Печать |
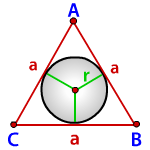
a - сторона треугольника
Радиус вписанной окружности в равносторонний треугольник (r):
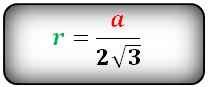
Радиус вписанной окружности в треугольник
| Печать |
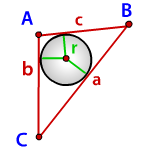
a, b, c - стороны треугольника
p - полупериметр, p=(a+b+c)/2
Радиус вписанной окружности в треугольник (r):