20. Якими математичними залежностями характеризуються ряди переважних чисел?
Ряди переважних чисел (у техніці) - це впорядкована послідовність чисел, призначена для уніфікації значень технічних параметрів.
При встановленні розмірів виробів широке застосування знайшли ряди чисел, побудовані на основі арифметичної чи геометричної прогресії.
Найпростіші ряди переважних чисел будуються на основі арифметичної прогресії — послідовності чисел, в якій різниця між наступним і попереднім членами ряду залишається постійною, тобто:
де U — значення членів ряду, що стоять поряд; d — різниця (інтервал) значень між двома суміжними членами ряду; n — порядковий номер члена ряду.
Будь-який член арифметичної прогресії можна обчислити за формулою:
де U1 — перший член арифметичної прогресії.
Графічно арифметична прогресія зображена прямою лінією (рис. 1.3).
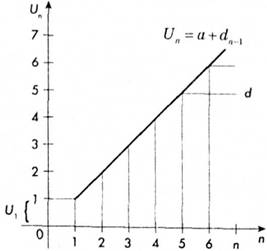
Рис. 1.3. Графік арифметичної прогресії
Позитивним у рядах арифметичної прогресії є те, що вони прості, не потребують округлення чисел. Але суттєвим недоліком є відносна нерівномірність. При сталій абсолютній різниці між членами ряду відносна нерівномірність різко зменшується. Так, відносна різниця між членами арифметичного ряду 1, 2 ... 9 для чисел 1 і 2 складає 100 %, а для чисел 9—10 — усього 11 %. Якщо зміну відносної різниці для членів цього ряду зобразити графічно, то отримаємо залежність, за якою при зростанні абсолютних значень членів арифметичного ряду відносна різниця зменшується (рис. 1.4).
Рис. 1.4. Залежність відносної різниці членів арифметичного ряду від їхнього місця у ряді
Ряди переважних чисел, основані на арифметичній прогресії, мало використовуються у параметричних стандартах. Вони застосовуються, наприклад, у стандартах розмірів взуття, діаметрів підшипників коливання, метричних різьблень, модулів зубчастих колес тощо.
Найбільш придатні для стандартизації параметрів і розмірів геометричні ряди чисел, які являють собою геометричну прогресію. Геометрична прогресія — це ряд чисел, в якому кожне наступне число отримується множенням попереднього на одне й те саме число, яке називається знаменником прогресії:
де U1 — перший член прогресії; Qn-1 — знаменник прогресії; п — порядковий номер взятого члена прогресії.
Ряд геометричної прогресії являє собою Q; Qх; Qх2; Qх3... Qхn-1 або 1, 2, 4, 8, 16, 32, 64..., де знаменником прогресії буде 2. Графік геометричної прогресії зображено на рис, 1.5.
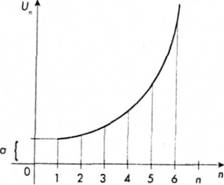
Рис. 1.5. Графік геометричної прогресії
Геометрична прогресія має ряд корисних властивостей.
1. Відносна різниця між будь-якими сусідніми членами ряду постійна. Кожний член прогресії більший за попередній на 100%.
2. Добуток чи частка будь-яких членів прогресії є членом цієї прогресії. Ця властивість використовується при пов'язуванні між собою параметрів і розмірів товарів, що підлягають стандартизації у межах одного ряду переважних чисел.
21. Дайте визначення терміна "переважні числа".
Перева́жні чи́сла — це числа, які рекомендується вибирати переважно перед всіма іншими при призначенні величин параметрів для новостворюваних виробів. Ці числа, побудовані за певною закономірністю, або ж із заокруглених значень ряду геометричної чи арифметичної прогресії в інтервалах, які використовують при встановленні градації відповідних параметрів (маси, розмірів, шкал, класів точності тощо). Використання переважних чисел і рядів має міжнародне значення. Параметричні ряди переважних чисел, або ж параметричні стандарти встановлюють ряди параметрів і розмірів найраціональніших типів і видів деталей, вузлів, машин, устаткування та ін. Для побудови рядів переважних чисел, крім геометричної прогресії, інколи використовують арифметичні, ступінчато-арифметичні прогресії і залежності. Ряди, побудовані за арифметичною прогресією, характерні тим, що різниця між сусідніми членами ряду залишається незмінною Ряди переважних чисел повинні відповідати наступним вимогам:
являти собою раціональну систему градацій, що відповідає потребам виготовлення та експлуатації виробів;
бути нескінченними, як у бік малих, так і великих чисел, тобто допускати встановлення безмежної кількості параметрів або розмірів у напрямку як збільшення їх значення, так і зменшення;
включати усі послідовні десятикратні чи дробові значення кожного числа ряду і одиницю;
Історія утворення рядів переважних чисел пов'язана з ім'ям офіцера французького інженерного корпусу Шарля Ренара, який у 1877-1879 рр. заклав наукові основи щодо використання переважних чисел для конструювання.