
- •1. Основные виды эконометрических моделей
- •2. Эконометрическое моделирование
- •3. Классификация видов
- •1. Общая модель парной регрессии
- •2. Нормальная линейная модель парной регрессии
- •3) Предположения о том, что дисперсия случайной ошибки уравнения регрессии является постоянной для всех наблюдеn ний и ковариация случайных ошибок любых двух разных набn
- •1. Классический метод наименьших квадратов для модели парной регрессии
- •2. Альтернативный метод нахождения параметров
- •1. Состоятельность и несмещенность мнКйоценок
- •2. Эффективность мнКйоценок. Теорема Гаусса—Маркова
- •1. Проверка гипотезы о значимости коэффициентов регрессии
2. Эффективность мнКйоценок. Теорема Гаусса—Маркова
С помощью теоремы Гаусса — Маркова доказывается эффекn тивность оценок неизвестных параметров уравнения регрессии, полученных с помощью МНК.
Нормальная, или классическая, линейная модель парной реn грессии (регрессии с одной переменной) строится исходя из слеn дующих предположений:
i
1) факторный признак x является неслучайной или детермиn
;
нированной величиной, не зависящей от распределения слуn
i
чайной ошибки уравнения регрессии
2) математическое ожидание случайной ошибки уравнения
i
регрессии равно нулю во всех наблюдениях: ( )0, где i1,n;
i
3) дисперсия случайной ошибки уравнения регрессии является постоянной для всех наблюдений: D( i )( 2 )G2 const;
27
,
4) случайные ошибки уравнения регрессии не коррелированы
между собой, т. е. ковариация случайных ошибок любых двух разnных наблюдений равна нулю: Cov( i, j )( ij )0, где ij. Это верно тогда, когда изучаемые данные не являются временn ными рядами;
i
5) основываясь на 3 и 4nм предположениях, добавляется услоn вие о том, что ошибка уравнения регрессии является случайn ной величиной, подчиняющейся нормальному закону распреn деления с нулевым математическим ожиданием и дисперсией G2 / ∼N(0,G2).
n
Тогда оценки неизвестных параметров уравнения регрессии, полученные методом наименьших квадратов, имеют наименьn шую дисперсию в классе всех линейных несмещенных оценок, т. е. оценки МНК являются эффективными оценками неизвестных параметров , ј, .Для нормальной линейной модели множественной регрессии теорема Гаусса — Маркова звучит точно так же.
Дисперсии МНКnоценок неизвестных параметров записыn ваются с помощью матрицы ковариаций. Матрица ковариаций МНКnоценок параметров линейной модели парной регрессии выглядит так:
Cov( )G2 ( 0 )
0
0 G2( 1)
где G2 ( 0 ) — дисперсия МНКnоценки параметра уравнения регрессии;
−
G2( 1) —дисперсия МНКnоценки параметра уравнения регрессии . Общая формула для расчета матрицы ковариаций МНКnоцеn
нок коэффициентов регрессии: Cov( )G2( )(XT X ) 1,
)
где G2 ( — дисперсия случайной ошибки уравнения регрессии. Рассмотрим процесс определения дисперсий оценок коэффиnциентов линейной модели парной регрессии, полученных с поn
мощью метода наименьших квадратов.
Дисперсия МНКnоценки коэффициента уравнения регрессии :
0
G x
)
(
2 2 G2() n 1G2 (x) ;
дисперсия МНКnоценки коэффициента уравнения регрессии :
28
(
)
2
G2( 1)n G G2(x),
где G2 ( ) — дисперnсия случайной ошибки уравнения регрессии ;
G2(x) — дисперсия независимого признака уравнения реn грессии;
n — объем выборочной совокупности.
На практике значение дисперсии случайной ошибки уравнеn
)
ния регрессии G2 (зачастую неизвестно, поэтому для опредеn ления матрицы ковариаций МНКnоценок применяют оценку дисперсии случайной ошибки уравнения регрессии S2( ). В слуn чае парной линейной регрессии оценка дисперсии случайной ошибки будет рассчитываться по формуле:
n
−
i
n
e2 G2( )S2( )i1 2 ,
i i i
где e2 y −y — остатки регрессионной модели.
Тогда общую формулу для расчета матрицы ковариаций МНКnоценок коэффициентов регрессии на основе оценки дисn персии случайной ошибки уравнения регрессии можно записать следующим образом:
−1
G( )S2( )(XT X) .
В случае линейной модели парной регрессии оценка дисперсии МНКnоценки коэффициента уравнения регрессии :
n n
i
2
e2 xi
n
0
1 1
S2 () i i ; n(n−2)(xi −x)2
1
i
оценка дисперсии МНКnоценки коэффициента уравнения реn грессии :
n
1
i
n
e2 S2() i1 .
(n−2)(xi −x)2
i 1
29
ЛЕКЦИЯ № 5. Определение качества модели
регрессии. Проверка гипотез о значимости коэффициентов регрессии, корреляции
и уравнения парной регрессии
Качество модели регрессии — адекватность построенной моn дели исходным (наблюдаемым) данным.
Качество парной линейной регрессии определяется с поn мощью парного линейного коэффициента корреляции:
r ,
xy−xy Cov(x, y ) yx G(x)G(y) G(x)G(y)
где G(x) — среднеквадратическое отклонение независимого призn нака;
G(y) — среднеквадратическое отклонение зависимого признака.
Коэффициент парной линейной корреляции можно рассчиn тать через МНКnоценку параметра уравнения регрессии :
r .
G(x) yx G(y)
−
yx
Парный коэффициент корреляции показывает тесноту связи между изучаемыми признаками. Он изменяется в пределах [−1; + 1]. Если r то связь между признаками прямая. Если ryx −, то связь между признаками обратная. Если ryx= 0, то связь между признаками отсутствует. Если ryx = 1 или C = 1,то связь между изучаемыми признаками является функциональной,
т. е. характеризуется полным соответствием между x и y. Чем блиn
же |rxy| к 1, тем более тесной считается связь между изучаемыми признаками.
Парный коэффициент корреляции определяется для количеn ственных переменных.
Если парный линейный коэффициент корреляции ryx возn
вести в квадрат, то получим коэффициент детерминации r2yx. Данный коэффициент показывает, на сколько процентов вариаn
ция результативного признака объясняется вариацией факторноn
го признака в общем объеме вариации.
Чтобы оценить качество линейной множественной модели реn грессии, необходимо воспользоваться теоремой о разложении дисперсий.
30
.
,
i
Общая дисперсия зависимой переменной может быть разлоn жена на две составляющие — объясненную и необъясненную поn строенным уравнением регрессии дисперсии:
G2(y)2(y)2(y),
где
n
(yi −yi )2
2
(y)i 1 n
— объясненная с помощью поn строенного уравнения регрессии дисперсия переменной y;
y
( )
i
n
— необъясненная или осn e2 таточная дисперсия переn 2 i 1 менной y. n
 С
помощью
данной
теоремы
можно
рассчитать
множественn
ный
коэффициент
корреляции
между
результативным
признаn
ком
y
и
несколькими
факторными
признаками
x:
С
помощью
данной
теоремы
можно
рассчитать
множественn
ный
коэффициент
корреляции
между
результативным
признаn
ком
y
и
несколькими
факторными
признаками
x:
Ry
2(y)
G2(y)
Множественный коэффициент корреляции показывает тесn ноту связи между результативным и факторными признаками. Трактовка его значений аналогична трактовке значений парного линейного коэффициента корреляции.
Квадрат множественного линейного коэффициента корреляn ции называется теоретическим коэффициентом детерминации:
R .
2
2 (y) y G2 (y)
y
Этот коэффициент показывает, на сколько процентов вариаn ция результативного признака объясняется вариацией факторn ных признаков x. Величина 1−R 2 показывает ту долю вариации
результативного признака, которую модель регрессии учесть не смогла.
n
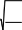 Среднеквадратическая
ошибка
(Mean
square
error
—
MSE)
уравнения
регрессии
схожа
по
построению
с
показателем
средГ
неквадратического
отклонения:
Среднеквадратическая
ошибка
(Mean
square
error
—
MSE)
уравнения
регрессии
схожа
по
построению
с
показателем
средГ
неквадратического
отклонения:
MSE
e2 i1
n−h
где h — число параметров уравнения регрессии.
31
Если MSEокажется меньше y, то построенную модель можn но считать качественной. Показатель среднеквадратического отn клонения наблюдаемых значений зависимой переменной от моn дельных значений, рассчитанных по уравнению регрессии, определяется как:
1
i
n
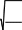 e2
(y)in
.
e2
(y)in
.
Показатель средней ошибки аппроксимации рассчитывается по формуле:
.
A
i
 1
n
y−y
y n
i1 yi
1
n
y−y
y n
i1 yi
Максимально допустимым значением данного показателя считается 12—15%. Если средняя ошибка аппроксимации составn ляет менее 6—7%, то качество модели считается хорошим.
