Символы состояний

Различные состояния электрона в атоме принято обозначать малыми буквами латинского алфавита в зависимости от значения орбитального квантового числа l

Квантовое число l	0	1	2	3	4	5
Символ состояния	s	p	d	f	g	h

Значение главного квантового числа п указывают перед символом состояния с данным числом l . Например, электрон, имеющий п = 3 и l =2 обозначают символом 3d. Последовательность имеет следующий вид:

1s (для п =1) 2s, 2p (для п = 2) 3s, 3p, 3d (для п = 3) и т.д.

10 - 3

Примеры некоторых нормированных волновых функций Ψ_nlm для ряда квантовых состояний водородоподобных атомов

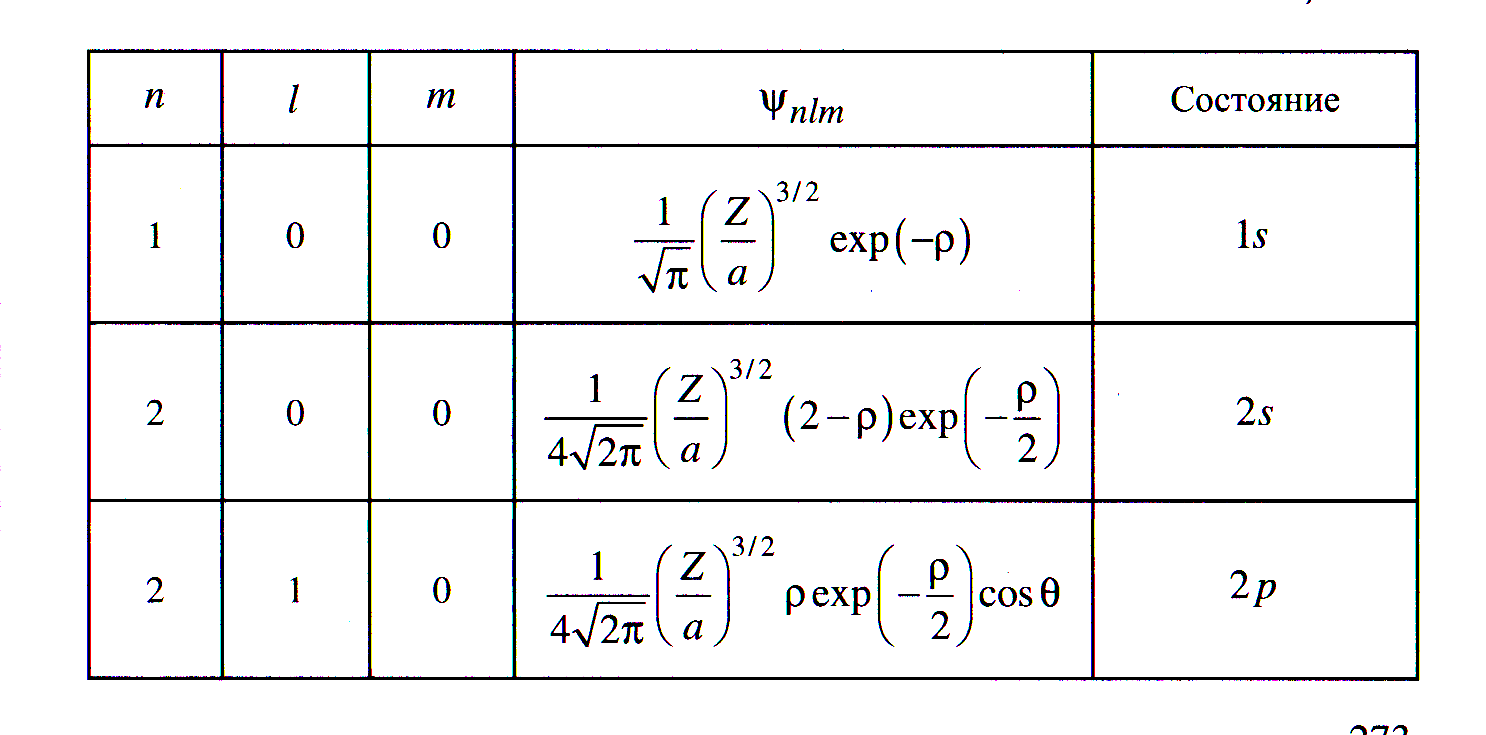
Здесь . Z – заряд ядра , r – расстояние от центра атома ,

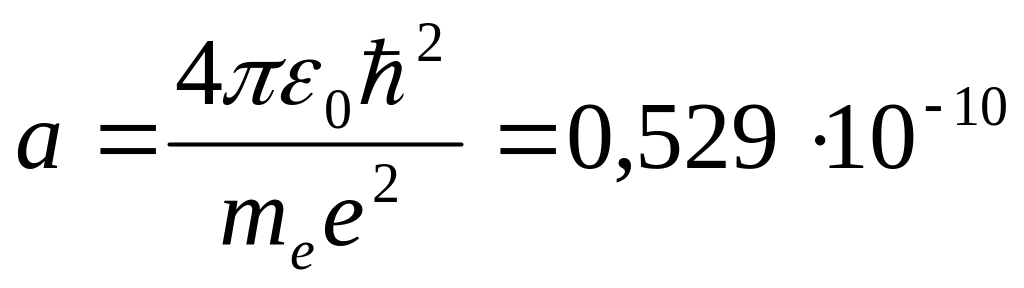м - универсальная константа, равная 1-ому

боровскому радиусу электрона в атоме

водорода.

Образ атома в квантовой теории может быть представлен в виде облака плотности вероятности

w =

П ространственное распределение плотности вероятности обнаружения электрона в различных квантовых состояниях атома водорода можно представить следующим образом

10 - 4

Орбитальный магнитный момент

Так как движущийся в классической теории Бора вокруг ядра электрон является заряженной частицей, то такое его движение обусловливает протекание некоторого замкнутого тока в атоме, который можно охарактеризовать орбитальным магнитным моментом р^м .

Для расчёта орбитального магнитного момента в квантовой теории следует определять пространственную плотность электрического тока через плотность потока вероятности

, где .

Связь механического и магнитного моментов определяется гиромагнитным отношением

.

Точный квантово-механический расчёт даёт ( причём это же выражение получается и из теории Бора )

.

Тогда

. где

0,927^.10^-23 Дж/Тл - магнетон Бора – универсальная постоянная, служащая единицей измерения магнитных моментов атомов.

Возмржные значения проекции магнитного момента атома на выделенное направление Z

р^м_z = m^.μ_Б .

10 – 5

Энергетический спектр электрона в атоме водорода

1 – переход в возбуждённое состояние

2 – ионизация атома W_i=-E₁ = 13,6 эВ

Ширина спектральных линий

Линии в спектре излучения атомов не являются бесконечно узкими – это соответствовало бы значению неопределённости ∆Е = 0, т.е. точно определённой энергии кванта излучения.

Спектральные линии, наблюдае-

мые в эксперименте, имеют конечную, так называемую естественную ширину линии Г , которая представляет собой разброс энергий фотонов относительно некоторого среднего значения, характе-

ризующего центр линии.

Эта ширина связана с временем жизни атома в возбуждённом состоянии соотношением

Экспериментальное определение ширины Г позволило оценить время с .