4.5 Перелік умовних позначень, символів, одиниць, скорочень і термінів

Якщо в ПЗ прийнята специфічна термінологія, а також використовуються мало поширені скорочення, нові символи, позначення, тощо, то їх перелік повинен бути представлений у ПЗ на окремому аркуші і розміщуватись після змісту.

Перелік повинен розташовуватись у вигляді стовпчика, в якому ліворуч в абетковому порядку наводять скорочення, символи, одиниці і терміни, праворуч – їх детальне розшифрування (пояснення).

4.6 Вступ

У вступі необхідно висвітити актуальність проблеми чи задачі, важливість для народного господарства об’єкта, що досліджується в курсовій робот, необхідність розроблення математичної моделі даного об’єкта.

4.7 Вказівки до виконання першого розділу курсової роботи

У цьому розділі описуються фізичні явища, які лежать в основі процесу, що досліджується шляхом розроблення математичної моделі. Обгрунтовується можливість застосування аналітичного моделювання для розроблення математичної моделі.

Опис явищ здійснюється на підставі положень фізики, хімії, біології (для біологічних об’єктів), електротехніки (для електричних об’єктів), механіки (для механічних об’єктів), а також вивчення літературних джерел, що стосуються специфіки заданого об’єкта, наприклад, гідравліки, аеродинаміки, акустики, пневматики, балістики та ін.

Описуються особливості застосування та фізичні основи функціонування об’єкта моделювання, закономірності взаємодії з іншими об’єктами.

4.7.1 Приклад 1. Опис фізичних явищ, які лежать в основі процесу утворення і поширення електромагнітної хвилі.

Збудження електричного поля за рахунок зміни магнітного поля і збудження магнітного поля за рахунок зміни електричного поля – призводять до того, що електромагнітне поле, яке змінюється в часі, разом з тим переміщається в просторі.

Припустимо, що в якій-небудь частині простору вже існує електромагнітне поле з взаємно перпендикулярно направленими електричним і магнітним полями, що змінюються в часі. Хай для якогось моменту часу це поле має вигляд, зображений на рис.4.1. На ньому напруженості полів зображені стрілками, а відстані відкладені по осі х. Крива, що огинає кінці стрілок, вказує на розподіл напруженості поля в просторі.

Рисунок 4.1 – Вигляд напруженостей електромагнітного поля

Зміна існуючого магнітного поля викличе появу електричного поля, яке напрямлене перпендикулярно до магнітного, але в різних частинах простору воно напрямлене в протилежні сторони (на рис. 4.2 це поле зображено пунктирними стрілками). В правій частині простору (рис. 4.2,а) виникле поле буде напрямлене так само, як існуюче електричне поле, і підсилить його, а в лівій частині виникле поле буде направлено вбік, протилежний напрямку існуючого поля, і тому послабить останнє. В результаті цього величини напруженості електричного поля в різних точках зміняться по траєкторії пунктирної лінії. Аналогічні зміни відбудуться і з магнітним полем. Зміни електричного поля викличуть появу перпендикулярного йому магнітного поля, яке в правій частині простору на рис. 4.2,б співпадатиме з напрямом існуючого магнітного поля, а в лівій частині буде протилежним існуючому магнітному полю.

Оскільки величини напруженості виниклих полів визначаються швидкостями зміни збудників цих полів, то у випадку, коли закон зміни обох полів однаковий, обидва поля зазнаватимуть однакових змін. І якщо обидва поля в початковий момент були однаковими (суцільні лінії на рис. 4.2,а і б мають однакову форму), то і нові поля в наступний момент також будуть однаковими, тобто обидві пунктирні лінії на рис. 4.2,а і б матимуть однакову форму і притому таку ж, як і суцільні лінії.

Рисунок 4.2 – Форми електричного і магнітного полів в різні моменти часу

Зміна в часі полів, як бачимо, призводить до того, що все електромагнітне поле як єдине ціле, не змінюючи своїх властивостей, зміститься вправо на деяку відстань d. Через такий же проміжок часу електромагнітне поле як єдине ціле зміститься ще на таку ж відстань d, і цей процес продовжуватиметься безкінечно довго. А це значить, що електромагнітне поле буде переміщуватися в просторі з деякою швидкістю, яка рівна зсуву d, розділеному на якийсь час, протягом якого цей зсув відбувається.

Напрям, в якому буде переміщуватися електромагнітне поле, залежить від взаємного орієнтування складових електричного і магнітного полів. При тих напрямах полів, які зображено на рис.4.1 (електричні поле — вгору, а магнітне — вперед від площини креслення), електромагнітне поле справді переміщуватиметься вправо. Якщо ж напрям одного з полів зміниться на протилежний, то і напрям переміщення електромагнітного поля зміниться на зворотній. В цьому можна переконатися, розглянувши, наприклад, електромагнітне поле, у якого електричне поле направлено як і раніше вгору, а магнітне — не вперед, а назад від площини креслення. На рис.4.3 для спрощення обидва ці поля зображені тільки однією стрілкою кожне. Оскільки напрям електричного поля залишився незмінним, то і напрям магнітного поля Н1, залишиться колишнім, тобто таким же, як на рис.4.2,б (на рис.4.3 — пунктирні стрілки).

Рисунок 4.3 – Зміна напрямку магнітного поля

З другого боку, оскільки напрям магнітного поля Н змінився на зворотній, то і напрям електричного поля Е1 зміняться на протилежний в порівнянні з тим, який був вказаний на рис.4.2,а. В цьому випадку виниклі поля справа послаблюватимуть, а зліва підсилюватимуть існуючі поля. Отже, електромагнітне поле переміщатиметься вліво, тобто в бік, протилежний тому, в який воно переміщалося в першому випадку.

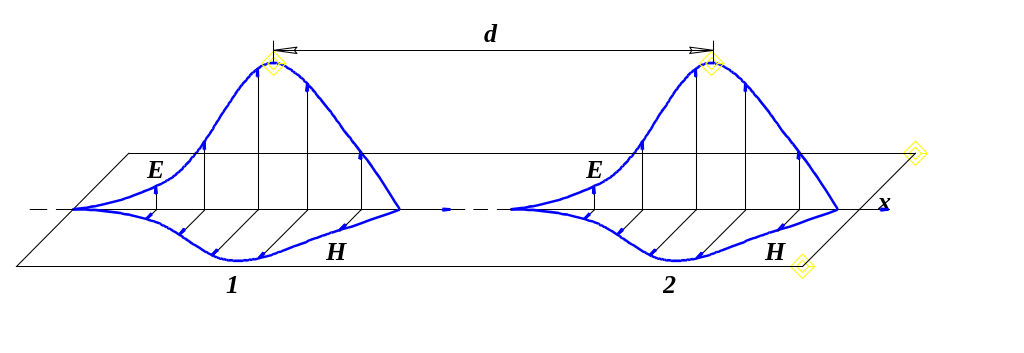
Вище було зроблено два істотні припущення. Перше, що в початковому електромагнітному полі електричне і магнітне поля направлені взаємно-перпендикулярно. Якби це було не так, то електричне і магнітне поля, порушувані змінами початкових магнітного і електричного полів, не співпадали б по напряму з початковими полями і картина вийшла б зовсім іншою. Наприклад, якщо обидва поля в початковий момент часу були напрямлені однаково, то поля, які б виникали при їх зміні, були перпендикулярні початковим. При цьому вони не могли б підсилювати початкове поле з одного боку і ослабляти його з іншого, тобто переміщення електромагнітного поля в просторі не відбувалося б. Таким чином, електромагнітне поле може переміщатися в просторі тільки тому, що електричне і магнітне поля є взаємно-перпендикулярними (рис. 4.4).

Рисунок 4.4 – Поширення електромагнітного поля

По-друге, що закон зміни обох полів в електромагнітному полі один і той же. Якби це було не так, то електромагнітне поле змінювало б свій характер при переміщенні (змінювалася б форма огинаючих). Таким чином, електромагнітне поле може перемішатися в просторі як єдине ціле, не змінюючи своєї форми, тільки за умови, що обидві складові цього поля змінюються за однаковим законом.

Отже, можна зробити висновок. Якщо в якомусь місці виникло електромагнітне поле (електричне і магнітне поля, які взаємно-перпендикулярні і змінюються по одному і тому ж закону), то це електромагнітне поле переміщається в просторі як єдине ціле (не змінюючи свого характеру) в напрямі, перпендикулярному напрямам електричного і магнітного полів, в бік, визначений правилом буравчика. Таке розповсюджуване в просторі електромагнітне поле називається електромагнітною хвилею.

Оскільки електричне і магнітне поля електромагнітної хвилі володіють енергією, то хвиля, розповсюджуючись в просторі, несе з собою цю енергію. Таким чином, електромагнітні хвилі є переносниками електромагнітної енергії.

4.8 Вказівки до виконання другого розділу курсової роботи

У цьому розділі виходячи з конкретної тематики курсової роботи та після опису фізичних явищ, які мають місце в заданому процесі, необхідно розробити математичну модель аналітичним методом та обгрунтувати вибір основних вхідних та вихідних параметрів

Приклад 2 Математичне моделювання процесу обертання посудини з рідиною навколо вертикальної осі

Візьмемо циліндр висотою Н і діаметром d=2R, наповнимо рідиною на висоту Н_п і розмістимо його в циліндричній системі координат r0z (рис.4.5).

Дослідимо закон зміни тиску і визначимо форму вільної поверхні рідини при обертанні даної посудини навколо її вертикальної осі z з подвійною кутовою швидкістю ω=2πn (n - кількість обертів посудини в секунду). Для цього в рідині виділимо точку А з координатами r_a і h_a. На дану точку рідини, крім сили ваги G=mg, буде діяти сила інерції F_ін=-ma, де a - доцентрове прискорення точки А. Одиничні масові сили в одному випадку, які діють на т. А, дорівнюють:

R=ω²r, (4.1)

Z=-g. (4.2)

Тоді диференціальне рівняння рівноваги рідини:

ρ(Xdx+Ydy+Zdz)=dp (4.3)

набуде вигляду:

dp=ρω²rdr-ρgdz (4.4)

Розв’язок рівняння (4.4) знаходимо в межах таких краєвих умов:

при r=r_a, h=h_a, p=p₁;

при r=0, h=h₀, p=p₀. (4.5)

де h₀ - відстань від дна посудини до вершини параболоїда обертання; p₀ - значення тиску на вільній поверхні рідини.

Після інтегрування одержимо:

(4.6)

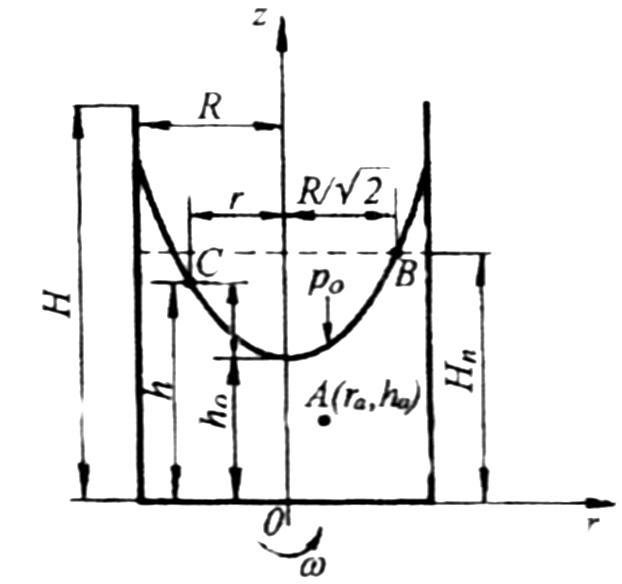
Рисунок 4.5 - Розміщення циліндра в циліндричній системі координат

Рівняння (4.6) описує закон зміни тиску в будь-якій точці рідини при обертанні посудини навколо своєї осі z з постійною кутовою швидкістю ω.

Встановимо форму вільної поверхні рідини при обертанні посудини навколо вертикальної осі. Для цього на вільній поверхні виділимо т. С з координатами r, h. Згідно з визначенням вільної поверхні dp=0. Тоді рівняння (4.4) буде мати вигляд:

ω²rdr=gdz (4.7)

Розв’язок рівняння (4.7) в межах вільної поверхні буде:

. (4.8)

З рівняння (4.8) видно, що вільна поверхня має форму параболоїда обертання. Позначимо через z=h-h₀ висоту параболоїда радіусом r. Тоді (4.8) має вигляд:

. (4.9)

При розв’язанні задач на відносний спокій рідини при обертанні відкритого циліндра (чи посудини іншої форми, наприклад, зрізаного конуса) навколо вертикальної осі можуть мати місце три випадки:

1. Вершина параболоїда обертання не доторкається до дна посудини (рис.4.6, а). Об’єм рідини, який знаходиться в посудині, при цьому дорівнює:

. (4.10)

2. Вершина параболоїда доторкнулась до дна посудини (рис.4.6, б)

. (4.11)

3. Вершина параболоїда перетнула дно посудини (рис.4.6, в)

. (4.12)

Для розв’язку диференціального рівняння (4.4) використаємо краєві умови типу:

при r=r_a, h=h_a, p=p;

при r= , h=Н_п, p=p₀. (4.13)

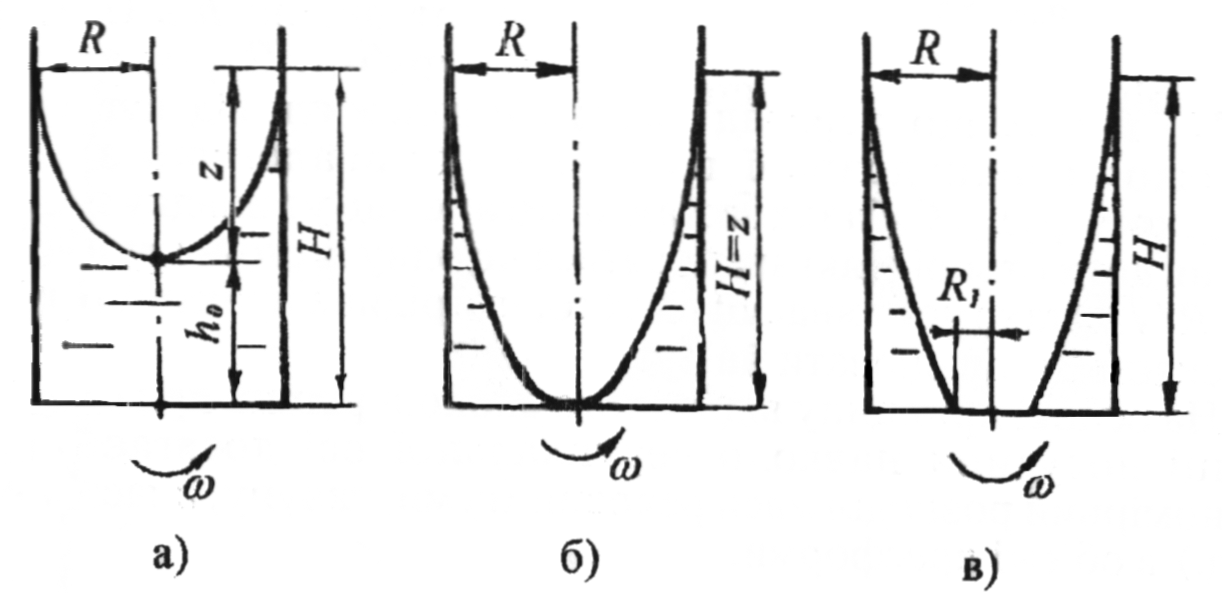
а - вершина параболоїда обертання не доторкається до дна посудини;

б - вершина параболоїда обертання доторкається до дна посудини;

в - вершина параболоїда обертання перетнула дно посудини.

Рисунок 4.6 - Розміщення вершин параболоїда обертання

Тоді розв’язок рівняння (4.4) за умови (4.13) має такий вигляд:

. (4.14)

На основі рівняння (4.14) можна легко пояснити принцип роботи рідинного тахометра. Тахометр представляє собою герметично закриту циліндричну посудину, яка повністю заповнена рідиною (рис. 4.7).

На кришці посудини знаходяться два отвори (центральний і периферійний), які з’єднані між собою U- подібною трубкою. При обертанні даного циліндра навколо своєї осі між даними точками створюється перепад тиску, який фіксується перепадом висот рідини h в U- подібній трубці. З рівняння (4.14) видно, що перепад висоти h залежить від кутової швидкості циліндричної посудини, що аналогічно зміні швидкості руху.

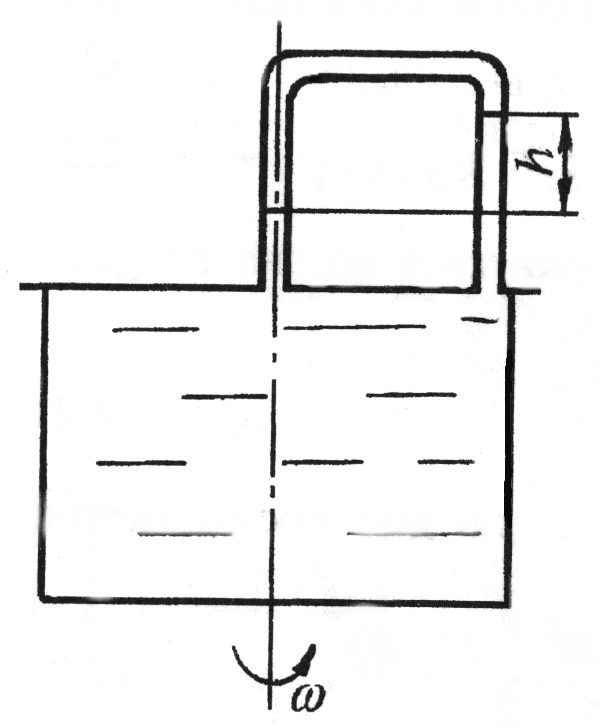
Рисунок 4.7 - Рідинний тахометр

Слід також зауважити те, що у випадку з’єднування двох отворів, які знаходяться по одну із сторін радіуса , тахометр внаслідок того, що рідина практично не стискається, працювати не буде.

4.9 Вказівки до виконання третього розділу курсової роботи

У цьому розділі необхідно дослідити адекватність, тобто відповідність моделі реальному фізичному процесу. Вказується повнота відтворення у моделі властивостей об’єкта, аналізується кількість та якість зроблених допущень та нехтувань і їх вплив на вірогідність моделі. Проводиться аналіз розробленої моделі.

Приклад 3 Дослідження адекватності моделі реальному процесу поширення електромагнітних хвиль

Обмеження, які накладаються на застосовність системи рівнянь Максвелла є такими: параметри  та , які характеризують властивості речовини в кожній точці, є незмінними в часі і не залежать від зміни температури та напруження зовнішнього поля. Враховуючи ці обмеження ми нехтуємо таким параметром як неоднорідність середовища в якому поширюється електромагнітна хвиля, адже на шляху поширення електромагнітної хвилі можуть зустрічатися повітряні маси з різними температурами та різним складом повітря, (наприклад хвиля проходить через хмару з дуже високою вологістю).

Також ми не враховуємо такі параметри як інтерференція та дифракція хвилі.

Інтерференція – явище, яке виникає внаслідок додавання хвиль і полягає в тому, що інтенсивність результуючої світлової хвилі (залежно від різниці фаз хвиль, які додаються) може бути більшою або меншою за суму їхніх інтенсивностей.

Дифракція – явище, пов’язане із зміною напряму поширення електромагнітних хвиль та з просторовим перерозподілом їх інтенсивності під впливом перешкод і неоднорідностей середовища на їхньому шляху.

У нашому випадку цими параметрами ми нехтуємо, так як ці фізичні явища не є суттєвими для представлення математичної моделі в найзагальнішому вигляді. Для нас є важливим показати сам закон, за яким поширюється електромагнітна хвиля в повітрі, а не її поведінку при зустрічі з різними перешкодами чи додаванні двох когерентних хвиль. Явище інтерференції та дифракції найбільш значуще для електромагнітних хвиль, які лежать в частотному діапазоні від 4·10¹⁴ до 6·10¹⁶ Гц.

Система рівнянь Максвелла є узагальненим математичним записом основних експериментальних законів електромагнітних явищ у довільному середовищі. Ці рівняння становлять основу розробленої Дж. Максвелом теорії макроскопічної електродинаміки, яку він послідовно вперше виклав у відомій праці „Трактат з електрики і магнетизму”, що вийшла у світ у 1873 р. Сучасного вигляду ці рівняння набули завдяки працям Г. Герца та англійського фізика О. Хевісайда (150 – 1925). Саме системою рівнянь Максвелла описуються електромагнітні хвилі в будь-якому середовищі.

У природі існують електромагнітні хвилі різних частот. Шкала електромагнітних хвиль становить безперервну зміну від нуля (нескінченно довгі хвилі постійних струмів) до 10²³ Гц (довжина хвилі 3·10^-15 м). Від довжини хвилі істотно залежить і її поширення. Короткі хвилі (λ ≈ 10 – 100 м) багаторазово відбиваються від іоносфери і поверхні Землі. Довгі хвилі „ковзають” по поверхні Землі. Ультракороткі хвилі проникають через іоносферу.