0

1. Что в физике понимают под полем, электрическим полем и зарядом?

2. Что означает и в чем проявляется потенциальный характер ЭСП?

3. Как и почему взаимосвязаны силовая и энергетическая характеристики ЭСП?

4. Почему потенциал, в отличие от напряженности, является непрерывной функцией координат?

5. Как и почему взаимоориентируются силовые линии и эквипотенциальные поверхности ЭСП?

6. Как соотносятся закон Кулона и теорема Остроградского – Гаусса

7. Как изменяются характеристики ЭСП в проводнике и диэлектрике?

8. Дайте сравнительную характеристику векторам напряженности, поляризованности и индукции ЭСП.

9. Как и почему преломляются силовые линии на границе раздела диэлектриков?

10. Каково физическое содержание понятия «электроемкость», и почему у проводника, в отличие от конденсатора, она зависит от окружающих тел и электрических полей?

11. Как и почему емкость сферического проводника зависит от его радиуса и заряда на нем?

12. Почему емкость конденсатора не зависит от напряжения (разности потенциалов) на нем?

13. Как и почему изменяется напряжение на конденсаторе при увеличении расстояния между его обкладками?

14. Почему при параллельном соединении конденсаторов емкость батареи больше чем при их последовательном соединении?

15. Как и почему энергия заряженного конденсатора зависит от его емкости?

16. Каково физическое содержание понятий «электросопротивление» и «удельное сопротивление»?

17. Почему у длинного проводника сопротивление больше чем у короткого?

18. В чем причины различия удельных сопротивлений у разных материалов?

19. Почему при последовательном соединении резисторов их результирующее электросопротивление больше чем при параллельном?

20. Объясните различия в правилах суммирования емкостей и сопротивлений при последовательном и параллельном соединении конденсаторов и резисторов.

21. Что общего и различного содержится в понятиях «разность потенциалов», «электродвижущая сила», «напряжение»?

22. Как и почему выделяемая током в проводнике теплота зависит от его сопротивления?

23. Как и почему полезная мощность и КПД источника тока зависят от силы тока в цепи?

24. Дайте сравнительную характеристику основным величинам электростатического и магнитостатического полей.

25. Что имеют общего и чем различаются понятия «электрический момент» и «магнитный момент»?

26. Дайте сравнительную характеристику силе Ампера и силе Лоренца.

27. Что имеют общего и чем различаются электрическая и магнитная проницаемости вещества?

28. Как и почему индуктивность катушки зависит от числа витков в ней?

1. Что в физике понимают под полем, электромагнитным полем и зарядом?

На уровне неживой природы материя – физическая реальность – существует в двух взаимосвязанных видах - вещества и поля. Вещество (тела, частицы) - дис­кретно, локализовано в пространстве, а поле (колебания, волны) - непрерывно распределено в пространстве, не обла­дая, ни формой, ни размерами.

Понятие поля было введено для объяснения с позиций концепции близкодействия (непосредственного действия) наблюдаемых в опыте фактов силового действия друг на друга пространственно разнесенных (не соприкасающихся непосредственно) вещественных тел.

Вещество способно порождать и поглощать поле, которое выступает в роли переносчика взаимодействия, осуществ­ляющего перенос и обмен движением между взаимодейст­вующими телами. Физическое поле подразделяется на четыре фун­даментальных вида: гравитационное, электромагнитное, сильное и слабое. Наиболее освоенным в современной практике и технике (особенно электро- и радиотехнике, электронике) является электромагнитное взаимодействие и его переносчик - электромагнитное поле. Оно является, например, причиной таких сил, как силы упругости и натяжения, силы трения и сопротивления.

В электромагнитном взаимодействии участвуют тела, обладающие электрическим зарядом и/или магнитным моментом. Такие тела создают в окружающем пространстве электромагнитное поле, которое проявляет себя в силовом действии (т. е. в изменении состояний движения) на другие тела, обладающие электрическим зарядом.

Электромагнитное взаимодействие и поле являются универсальными, т. к. все три элементар­ные частицы атомов вещества (электрон, протон и нейтрон) обладают магнитным моментом, а элек­трон и протон - и электрическим зарядом.

Электростатическое поле (ЭСП) - простейший вид (состояние) электромагнитного поля, порождаемый и неразрывно связанный с неподвижными (в данной системе отсчета) электрически заряженными телами, существующий в окружающем их пространстве и проявляющий себя в силовом действии на другие заряженные тела.

Электрический заряд является характеристикой тел, определяющей меру интенсивности участия их в электромагнитном взаимодействии. Чем больше значение заряда тела, тем сильнее создаваемое им электрическое поле, и тем с большей силой оно взаимодействует с другими электрическими полями.

2. Что означает и в чем проявляется потенциальный характер эсп?

Потенциальным называют поле, силы которого являются консервативными, т. е. их работа не зависит от формы траектории, а определяется лишь положениями начальной и конечной точек перемещения и равна нулю по замкнутой траекто­рии. Консервативность сил электростатического взаимодействия вытекает из закона Кулона, согласно которому, силы электростатического взаимодействия между точечными зарядами являются центральными (радиальными), т. е. ~ . В механике показывалось, что такие силы являются консервативными. Такое поле можно характеризовать и силовой - напряженностью , и энергетической - потенциалом  - величинами, являющимися полевыми функциями, т.е. функциями точки, положения в поле.

3. Как и почему взаимосвязаны силовая и энергетическая характеристики эсп?

Силовая характеристика ЭСП - напряженность - удельная по заряду сила, т. е. сила, дейст­вующая со стороны поля на единичный неподвижный положительный заряд в данной точке поля:

= /q  единица напряженности [Н/Кл].

Энергетическая характеристика ЭСП - потенциал  может быть получена из известного в механике выражения, связывающего силу и потенциальную энергию, в соответствии с которым, сила есть антиградиент потенциальной энергии (или проекция силы на некоторое направление равна быстроте убыли потенциальной энергии W_п в данном направлении):

= - grad W_п  /q = - grad W_п/q  = - grad 

Напряженность есть антиградиент потенциала, где за потенциал  принято отношение потенциальной энергии (энергии взаимодействия заряда с полем) к значению заряда:  = W_п/q - удельная по заряду потенциальная энергия, то есть потенциальная энер­гия единичного положительного заряда в данной точке поля, измеряемая в вольтах: [] = Дж/Кл = В. о

В проекции векторного равенства = - grad , например, на ось имеем: Е_х = - /х. В соответствии с этим выражением про­екция напряженности есть быстрота убыли потенциала в соответствующем направлении. Отсюда для напряженности получа­ет иное выражение и трактовку ее единица: [Е] = [В/м], которая показывает, на сколько вольт убывает потенциал на еди­нице длины в соответствующем направлении.

Обратный переход от напряженности к разности потенциалов, выража­ется интегральным соотношением: из d = - Е_хdх   = ₂ - ₁ = 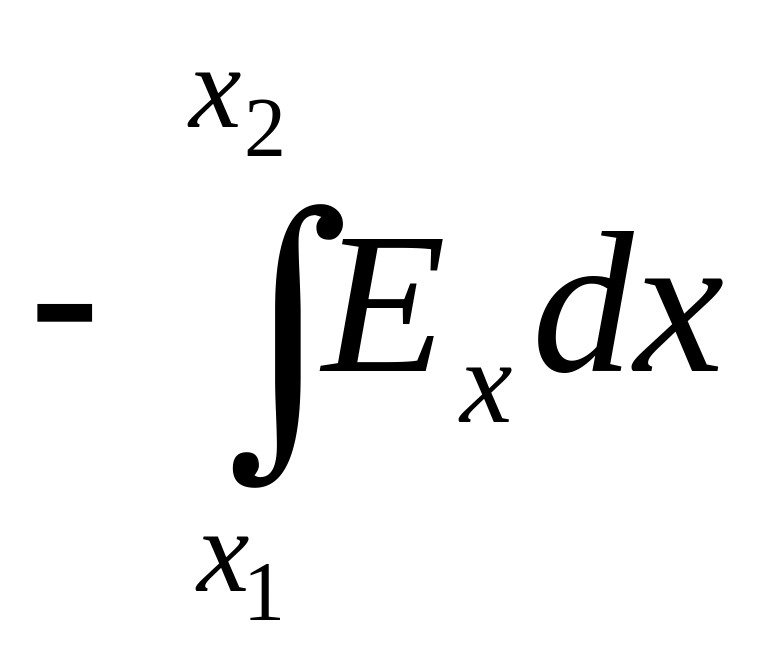или ₁ - ₂ =

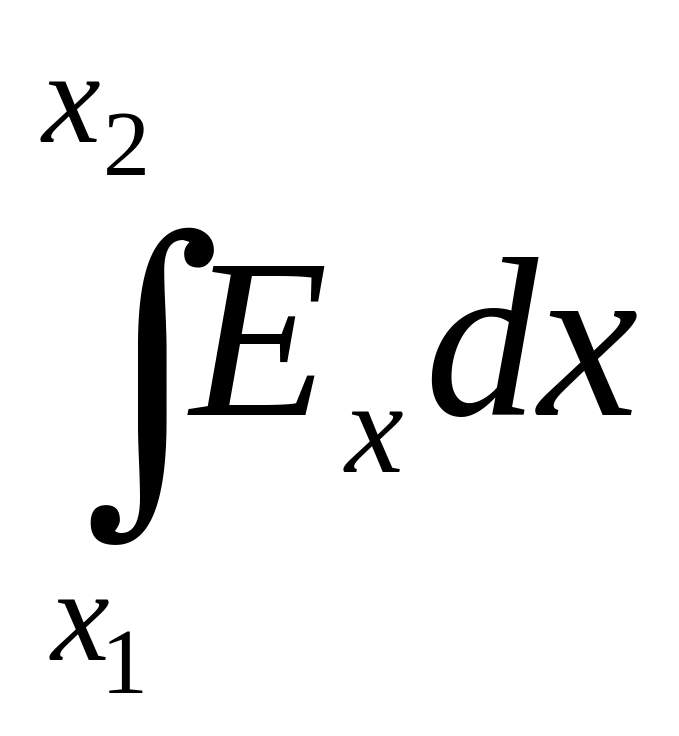
Для однородного ЭСП, напряженность в котором во всех точках одинакова, взаимосвязь между силовой и энергетической характеристиками упрощается:

Е_х = - /х = (₁ - ₂)/(х₂ - х₁) или Е = U/d, а U = Еd, где U = ₁ - ₂ называют еще напряжением, а d = х₂ - х₁ – расстояние между двумя точками поля.

4. Почему потенциал, в отличие от напряженности, является непрерывной функцией координат? Если предположить обратное, то есть, что потенциал может быть разрывной функцией координат, например координаты х, тогда в точке разрыва, при dх = 0, d  0. А это означает, что в этой точке напряженность обращается в бесконечность: Е_х = - d/dх = . Но этого не может быть, бесконечно большое значение напряженности противоречит условиям физической реализуемости.

5. Как и почему взаимоориентируются силовые линии и эквипотенциальные поверхности ЭСП? Силовые линии – линии, касательные к которым сов­падают с направлением вектора в каждой точке поля, а их густота пропорциональна числен­ному значению напряженности ЭСП в данном месте. Эквипотенциальные поверхно­сти - поверхно­сти, все точки которых имеют одинаковый потенциал. Характерным для ЭСП является перпен­дикуляр­ность силовых линий эквипотенциальным поверхностям. Это следует из того, что вдоль эквипотен­циальной поверхности  = const, то есть d = 0, а значит проекция Е_ вектора на эквипотенциальную поверхность Е_ = - d/d = 0. Отсюда вектор должен быть перпендикулярен эквипо­тен­циальной поверхности.

Силовые линии направлены в сторону убыли потенциала, от большего его значения к мень­шему. Это следует из взаимосвязи напряженности и потенциала, в соответствии, с кото­рой напряженность есть антиградиент потенциала, а градиент, по определению, есть вектор, направ­ленный в сторону наибыстрейшего возрастания функции (в данном случае – потенциала). Из = - d/dх при dх  0 и d  0   , то есть вектор направлен против оси Х, против направления возрастания потенциала .

6. Как соотносятся закон Кулона и теорема Остроградского – Гаусса? Основной закон электростатики - закон Кулона - устанавливает характер сил элек­тро­статического взаимодействия на элементарном уровне, т. е. на уровне точечных неподвиж­ных заряженных тел (точечных зарядов):

г

= - = kq₁q₂ /

де, а - вектор, соединяющий первый заряд

со вторым (q₁ и q₂).

Согласно закону Кулона, силы электростатического взаимодействия между точечными заря­дами в однородной изотропной среде обратно квадратичны удалению,

т. е.F₁₂=F₂₁= F ~ 1/r₁₂².

Следствием этого «закона обратных квадратов» является теорема Остроградского – Гаусса, связывающая поток вектора с зарядом, его обусловливающим.

Таким образом, эта теорема может рассматриваться как следствие закона Кулона, но это справедливо лишь в электростатике, где заряды, создающие электрические поля, неподвижны. Но она оказывается справедливой и в электродинамике (где заряды могут двигаться с ускорением и создавать переменные электрические поля), то есть она более обща, чем закон Кулона.

И закон Кулона, и теорема Остроградского – Гаусса является эффективными инструментами решения основной задачи электростатики - расчета характеристик ЭСП по заданному распределению в пространстве его источников – электрических зарядов.

Из закона Кулона вытекает важная в силу своей элементарности формула для напряженности ЭСП точечного (и сферического) заряда: = kq/(r²) /r , где - радиус вектор точки поля

относительно заряда – источника поля.

Т. к. любое реальное заряженное тело можно представить состоящим из заряженных точеч­ных частиц, то, зная характеристики ЭСП точечного заряда и правила их суммирования (прин­цип суперпозиции), можно определять характеристики результирующего ЭСП, создаваемого всем заря­женным телом в целом. При наличии неточечных источников ЭСП расчет их характеристик с помощью закона Кулона и принципа суперпозиции обычно наталкивается на значительные мате­ма­тические трудности. Во многих случаях более просто характеристики их ЭСП вычисляются с помощью теоремы Остроградского – Гаусса, носящей скалярный харак­тер. Так как для определения трех неизвестных (Е_х, Е_у и Е_z - составляющих вектора ) одного урав­нения недостаточно, то применение этой теоремы дополнительно требует определенной симметрии поля и его источников.