3. Вычисление параметров линейного уравнения множественной регрессии.
Эта операция проводится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии, а отличие от парной регрессии состоит только в том, что в диалоговом окне при заполнении параметров входной интервал Х следует указывать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены на рис. 5. 4.
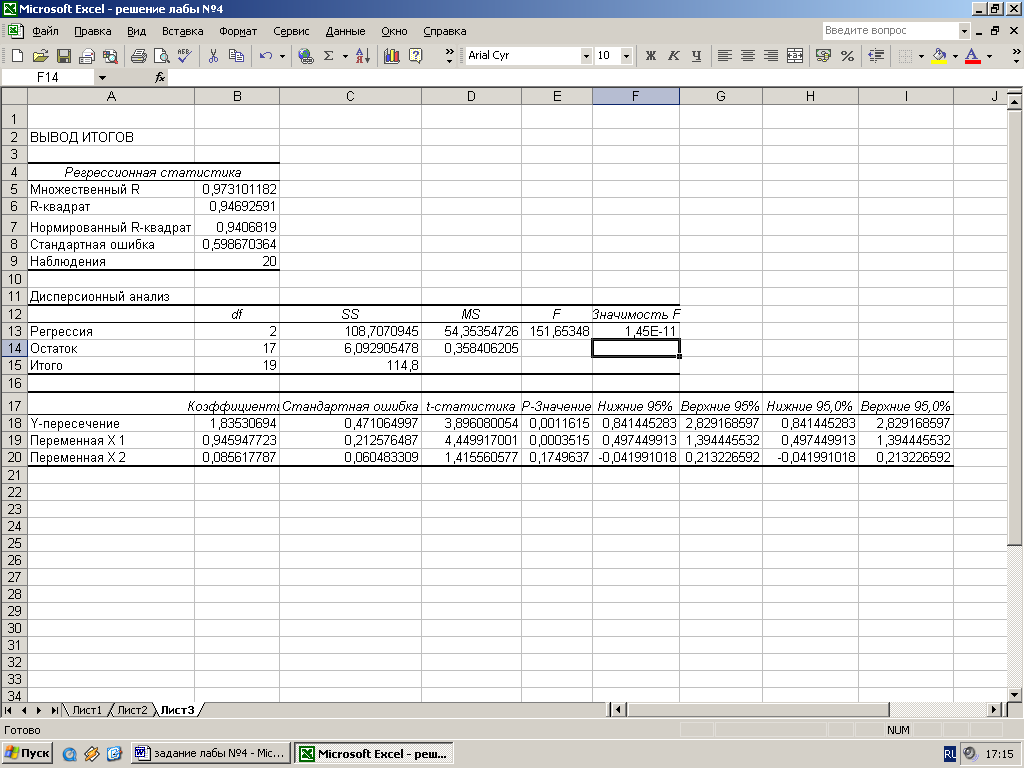
Рис. 5.4. Результат применения инструмента Регрессия
По результатам вычислений составим уравнение множественной регрессии вида
;
.
Величина
оценивает агрегированное влияние прочих
(кроме учтенных в модели факторов
и
)
факторов на результат y.
Величины
и
указывают, что с увеличением
и
на
единицу
результат
увеличивается соответственно на 0,9459 и
0,0856 млн. руб. Сравнивать эти значения
не следует, т.к. они зависят от единиц
измерения каждого признака и потому
несопоставимы между собой.
Значения
случайных ошибок параметров
,
и
с учетом округления составят:
,
,
.
Они показывают, какое значение данной
характеристики сформировалось под
влиянием случайных факторов. Эти значения
используются для расчета t-критерия
Стьюдента
;
;
.
Если
значения t
- критерия больше 2 - 3, можно сделать
вывод о существенности данного параметра,
который формируется под воздействием
неслучайных причин. Здесь статистически
значимыми являются
и
,
а величина
сформировалась под воздействием
случайных причин, поэтому фактор
,
силу влияния которого оценивает
,
можно исключить как несущественно
влияющий, неинформативный.
На
это же указывает показатель вероятности
случайных значений параметров регрессии:
если
меньше принятого нами уровня (обычно
0,1; 0,05 или 0,01; это соответствует 10%, 5% или
1% вероятности), делают вывод о несущественной
природе данного значения параметра,
т.е. о том, что он статистически значим
и надежен. В противном случае принимается
гипотеза о случайной природе значения
коэффициентов уровня. Здесь
> 5%, что позволяет рассматривать
как неинформативный фактор и удалить
его для улучшения данного уравнения.
4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает f-критерий Фишера:
По
данным таблицы дисперсионного анализа,
представленной на рис. 5.4,
=151,65.
Вероятность случайно получить такое
значение F-критерия
составляет 0 (см. значимость F),
что не превышает допустимый уровень
значимости 5%; об этом свидетельствует
величина Р
- значение
из этой же таблицы. Следовательно,
полученное значение неслучайно, оно
сформировалось под влиянием существенных
факторов, т.е. подтверждается статистическая
значимость всего уравнения и показателя
тесноты связи
.
Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 5. 4 в рамках регрессионной статистики. Нескорректированный коэффициент множественной детерминации =0,9469 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.
Скорректированный коэффициент множественной детерминации =0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата y в модели факторами и .
5. Информация для оценки с помощью частных F- критериев Фишера целесообразности включения в модель фактора после фактора и фактора после фактора может быть получена в ППП Statgraphics. Частный F- критерий показывает статистическую значимость включения фактора после того, как в нее включен фактор .
Но по данным, вычисленным с помощью ППП Excel, можно сделать общий вывод, который состоит в том, что множественная модель с факторами и с =0,9469 содержит неинформативный фактор . Если исключить фактор , то можно ограничиться уравнением парной регрессии более простым, хорошо детерминированным, пригодным для анализа и для прогноза.
6.
Средние
частные коэффициенты эластичности
показывают, на сколько процентов от
значения своей средней
изменяется результат при изменении
фактора
на
1% от своей средней
и при фиксированном воздействии на у
всех прочих факторов, включенных в
уравнение регрессии. Для линейной
зависимости
,
(5.1)
где
-
коэффициент регрессии при
в уравнении множественной регрессии.
Здесь
,
.
По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у признака фактора , чем признака фактора : 0,6% против 0,2%.
3. Задание лабораторной работы.
В предлагаемых по вариантам задачах необходимо составить прогноз социально-экономического развития анализируемого показателя по методу многомерной регрессии, используя последовательность аналитических расчетов представленного практического примера.