2.4 Графическое оценивание параметров нормального распределения
По
формуле
находим
значения F(xi)
и на Рисунок 3 наносим точки с координатами
[xi;100F(xi)].
На Рисунок 3 наносим точки с координатами [1;3,5], [4;10], [5;16], [7;28], [11;35], [12;41], [12;47], [13;53], [14;59], [14;65], [16;72], [41;78], [44;84], [49;90], [74;96].
Так как через нанесенные точки возможно провести прямую, то делаем заключение, что данная выборка принадлежит к нормальному распределению.
Оценкой
параметра
нормального распределения является
абсцисса точки на прямой с ординатой
[100 F(x)=12 или [Uq=0] =14.
Абсциссы
точек на прямой с ординатами [Uq=+1]
определяют параметр
:
Рисунок 3 - Графическое оценивание параметров распределения Вейбулла
3 Оценивание показателей безотказности
Значения показателей безотказности, определяемые по результатам испытаний, являются оценками показателей надёжности.
За значения показателей надёжности принимают точечную оценку или границы доверительного интервала нижнюю (НДГ) и верхнюю (ВДГ) границы.
Вычисление точечных оценок и НДГ осуществляется по следующим формулам.
Экспоненциальное распределение:
Средняя наработка:
Нижняя
доверительная граница средней наработки:
Гамма-процентная наработка:
Вероятность безотказной работы:
Интенсивность отказов:
Распределение Вейбулла:
Средняя наработка:
Нижняя доверительная граница средней наработки:
Гамма-процентная наработка:
Вероятность безотказной работы:
Интенсивность отказов:
Нормальное распределение:
Интенсивность отказов:
Вероятность безотказной работы:
4 Восстановление работоспособного состояния
Металлургическое оборудование является восстанавливаемой системой и поэтому, время её функционирования во много раз больше средней наработки на отказ. В этом случае среднее число отказов на интервале [0,t] приближённо равно
;
Система
восстанавливается путём замены входящего
в его состав отказавшего элемента и
функционирует время
,
то необходимое число запасных элементов
,
необходимых для непрерывной работы
системы до момента времени
равно
При подсчёте запасных частей на год принимать q = 0,95, на месяц – q = 0,975.
Для определения гарантированного количества запасных частей, предотвращающее их истощение за определенный промежуток времени, используется распределение Пуассона, которое позволяет подсчитать вероятность отказов менее r, или равных r подсчитать вероятность менее r или равных r отказов, за определенный промежуток времени:
;
и вероятность более r отказов:
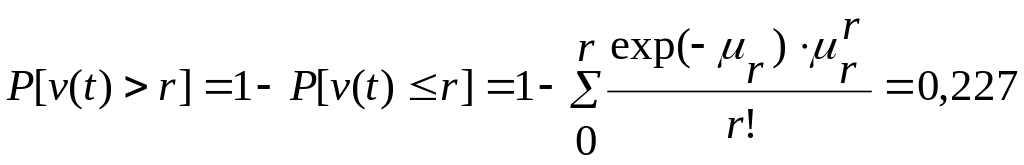
Список литературы
1. Жиркин Ю.В. Надёжность, эксплуатация и ремонт металлургических машин. Учебник. Магнитогорск: МГТУ. 2002г..
2. Жиркин Ю.В. Надёжность, эксплуатация, техническое обслуживание и ремонт металлургических машин. Магнитогорск, МГТУ, 1998.
3. Жиркин Ю.В. Сборник задач и упражнений по курсу «Надёжность, ремонт и монтаж металлургических машин». Свердловск: УПИ, 1986.