6. Определение основных размеров стрелочного перевода

К основным размерам относятся:

1) теоретическая длина стрелочного перевода;

2) полная длина стрелочного перевода.

Теоретическая длина стрелочного перевода L_t , то есть расстояние от начала остряка до математического центра крестовины при R ≠ R₀, определяется по формуле:

, (6.1)

Теоретическая длина стрелочного перевода L_t при R = R₀, определяется по формуле:

, (6.2)

Полная длина стрелочного перевода Lp в обоих случаях равна:

, (6.3)

7. Определение осевых размеров стрелочного перевода

Для разбивки перевода на местности необходимо знать его осевые размеры. К осевым размерам относятся:

1) расстояние от центра перевода до острия пера остряков;

2) расстояние от центра перевода до конца рамного рельса;

3) расстояние от центра перевода до математического центра крестовины;

4) расстояние от центра перевода до конца хвостовой части крестовины.

Расстояние от острия пера остряков до центра перевода а_о (рис. 7.1) определяется по формуле

, (7.1)

Расстояние от центра перевода до конца рамного рельса а определяется по формуле

, (7.2)

Расстояние от центра перевода до математического центра крестовины b_o определяется по формуле

, (7.3)

Расстояние от центра перевода до конца хвостовой части крестовины b определяется по формуле

, (7.4)

Отсюда следует, что .

Рис.7.1 Осевые размеры

Расстояния go и g (рис.7.2), определяющие местоположение предельного столбика, который устанавливается в междупутье, где его величина достигает 4100 мм, находятся по формулам:

, (7.5)

, (7.6)

где N – знаменатель марки крестовины.

Рис. 7.2. Определение местоположения предельного столбика.

8. Определение координат для разбивки переводной кривой стрелочного перевода

Соединительная часть между стрелкой и крестовиной состоит из переводной кривой и части прямой вставки. Переводные кривые обычно устраиваются по круговой кривой. Переводная кривая по наружной рельсовой нити укладывается по координатам. Расчетная схема представлена на рис. 8.1.

Координаты наружной, или упорной нити переводной кривой определяются в следующей последовательности:

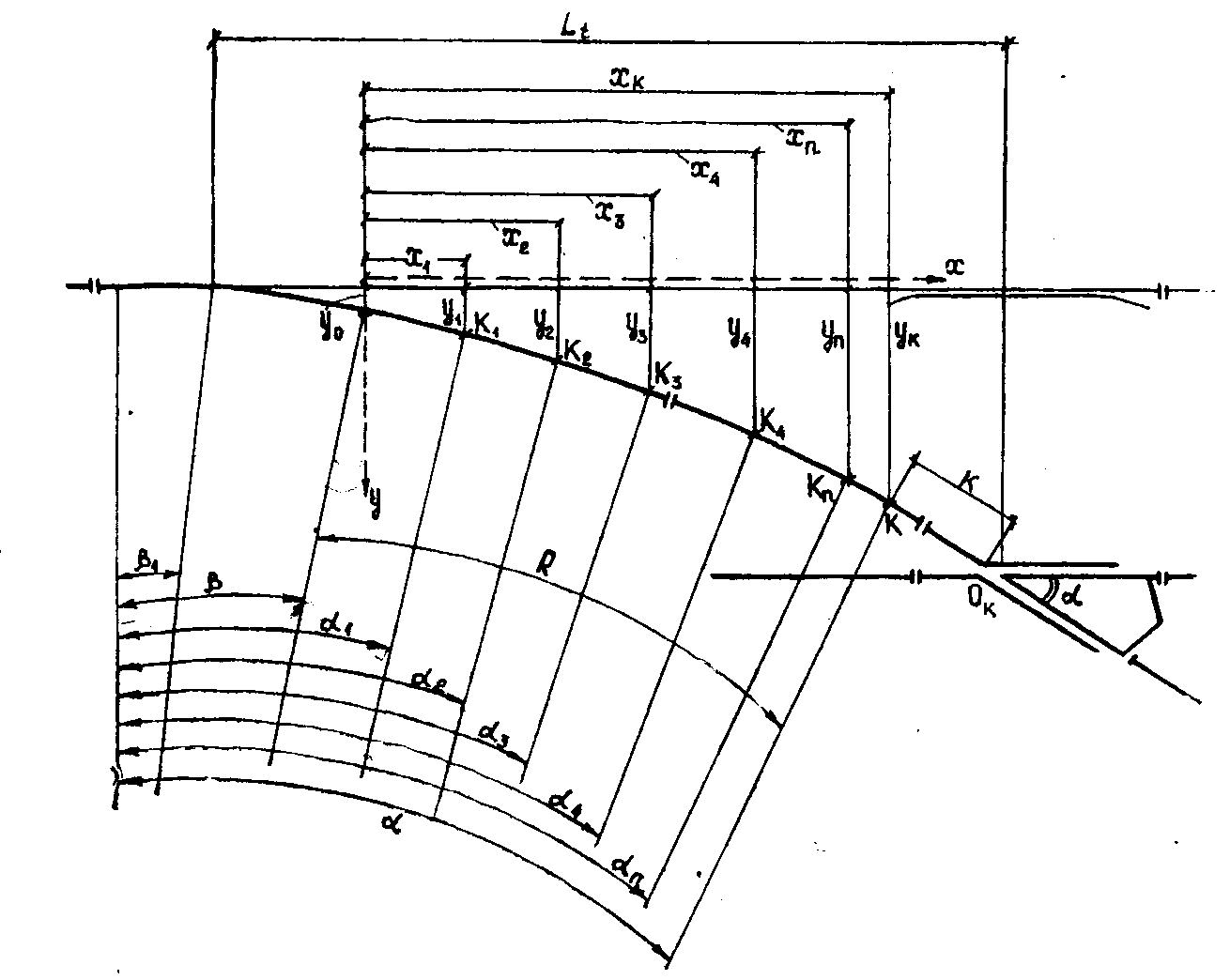Рис.8.2. Расчетная схема для определения координат переводной кривой

1) начало прямоугольной системы координат для разбивки переводной кривой располагается на рабочей грани рамного рельса против корневого стыка остряка, точка О₀ (см. рис. 8.2).

Рис. 8.2. Построение прямоугольной системы координат для разбивки переводной кривой

2) Из точки начала координат откладывают абсциссы и вычисляют соответствующие им ординаты. Значениями абсцисс X_i задаемся через каждые два метра.

X₀ = 0;

X₁ = 2000 мм;

X₂ = 2 х 2000 мм = 4000 мм;

X₃ = 3 х 2000 мм = 6000мм;

…………………………………

X_i = i х 2000 мм = i х 2000 мм;

………………………………….

Х_k = R_пр(sin α – sin β)

3) Вычисляются соответствующие ординаты Y_i:

Y₀ = R₀ (cos β_н - cos β ) = U.

Y₁ = Y₀ + R_пр (cos β - cos γ₁ );

Y₂ = Y₀ + R_пр (cos β - cos γ₂ );

………………………………

Y_i = Y₀ + R_пр (cos β - cos γ_i );

………………………………

Y_k = Y₀ + R_пр (cos β- cos α ).

4) Вспомогательные углы γ_i определяются из выражения:

sin γ_i = sin β + x_i / R_пр,

например:

sin γ₁ = sin β + x₁ / R_пр;

sin γ₂ = sin β + x₂ / R_пр и т.д.

5) Расчет координат переводной кривой рекомендуется выполнять в табличной форме (табл.8.1).

Таблица 8.1