По аналогии с этим могут быть представлены и выражения для Y₂ и Y с учетом активно-емкостного характера сопротивле­ний во второй ветви цепи Y₂ =

[R₂/(Z₂)²] – j[(X_L2 – X_C2)/(Z₂)²] = G₂ +jB₂, Y = [R/(Z)²] – j[(X_L – X_C)/(Z₂)²] = G – jB.

при Х_C2 > X_L2. и Х_C < Х_L (см. рис. 4.2): при этом Y=Y₁ +Y₂ = (G₁+ G₂) -j(B₁ – B₂) = G – jB. Отсюда в общем случае для произвольного числа параллель­ных ветвей активная проводимость электрической цепи при па­раллельном соединении сопротивлений оказывается равной сум­ме активных проводимостей всех параллельных ветвей, а реактивная проводимость цепи равной алгебраической сумме ре­активных проводимостей всех параллельных ветвей, входящих в

данную электрическую цепь

Модуль полной проводимости цепи определяется из выраже­ния

Полная проводимость цепи в то же время является и величи­ной, обратной ее полному сопротивлению Y = l/Z. Разделив каждый вектор тока на векторной диаграмме рис. 4.2 на вектор напряжения U, можно получить треугольник проводимостей для данной цепи. В качестве примера на рис. 4.3 представлен треугольник проводимостей для первой ветви схемы рис. 4.1. Из треугольника проводимостей следует, что cos φ₁ = G₁ /Y₁, a sin φ₁ = B₁/ Y₁ = (B_L1-B_C1)/Y₁. С учетом этого полная, активная и ре­активная мощности цепи могут быть определены через соответ­ствующие проводимости: S₁= UI₁ = U²Y₁, P₁ = UI₁ cos φ₁ = U²G₁, Q₁ = UI₁ sin φ₁ = U²B₁.

В электрических цепях переменного тока при параллельном соединении ре­активных сопротивлений может возни­кать резонанс токов. Это происходит в том случае, когда в одних ветвях преоб­ладает реактивное индуктивное сопро­тивление, а в других — реактивное ем­костное сопротивление. Резонанс токов (явление резонанса на участке электри­ческой цепи, содержащей параллельно

соединенные индуктивный и емкостный элементы) — особое со­стояние цепи переменного тока при параллельном соединении сопротивлений, при котором реактивная индуктивная проводи­мость оказывается равной реактивной емкостной проводимости этой цепи, т. е. при условии, что В_L= В_C. Простейшей электрической цепью, в которой может наблю­даться резонанс токов, является цепь с параллельным соединени­ем катушки индуктивности и конденсатора.

Полная проводимость рассматриваемой цепи

Условие резонанса токов В_L= В_C. можно записать через соот­ветствующие параметры электрической цепи. Так как реактивная проводимость катушки, имеющей активное сопротивление R_K, определяется выражением B_L= X_L/(Z_K)² = ωL / (R_K + ω²L²), а проводи­мость конденсатора без учета его активного сопротивления R_C = 0). B_C = X_C/(Z_C)² = 1/X_C = ωC, то условие резонанса может быть записано в виде ωL / (R_K + ω²L²) = ωC. Из этого выражения следует, что резонанс токов можно полу­чить при изменении одного из параметров R_K, L, С и ω при по­стоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении ука­занных параметров.

Простейшие резонансные цепи, состоящие из параллельно со­единенных между собой катушки индуктивности и конденсатора, широко применяют в радиоэлектронике в качестве колебатель­ных контуров, в которых резонанс токов достигается при некото­рой определенной частоте поступающего на вход соответствую­щего устройства сигнала. В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности L катушки, путем изменения емкости С батареи конденсаторов. С изменением ем­костной проводимости B_C ≈ ωC, пропорциональной емкости кон­денсатора, происходит изменение полной проводимости Y, общего тока I и коэффициента мощности cos φ.

Указанные зависимости называются резонансными кривыми (рис. 4.4). Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость элек­трической цепи сначала уменьшается, достигает при В_C = В_L сво­его минимума, а затем возрастает с увеличением С, в пределе

ЛАБОРАТОРНАЯ РАБОТА № 15

Исследование однофазных неуправляемых источников вторичного электропитания электронных устройств

15.1.Цель работы

Изучить принцип выпрямления электрических колебаний. Проверить экспериментально принцип действия неуправляемых выпрямителей.

15.2. Задание по работе

1. Изучите описание данной работы.

2. Ответьте на все вопросы для самопроверки.

3. Нарисуйте схему неуправляемых однополупериодного и мостового выпрямителей

4. Нарисуйте временные диаграммы исследуемых выпрями­телей.

5. Рассчитайте средние значения выпрямленных напряже­ний и тока, средний и максимальный ток диода, максималь­ное обратное напряжение на диоде, коэффициент пульсации выпрямителей без фильтра. Данные для расчета брать из табл.15.1.

Таблица 15.1

Исходные данные для расчета

Номер бригады	Тип диода	Выходное напрж. U2 В	Сопротивление нагруз. RН. Ом
1	Д 211	20	100
2	Д 7	20	150
3	Д 226 В	20	200
4	Д 226 Б	20	250

15.3. Основные теоретические положения

Выпрямительные устройства служат для преобразования синусоидальных напряжений и токов. Различают неуправляе­мые и управляемые выпрямительные устройства. В неуправ­ляемых выпрямителях используются диоды, а в управляемых - тиристоры.

Если источник э.д.с. синусоидальный, то U(t) = U_m sin ωt, а диод будем считать идеальным, то в нагрузке потечет ток I(t) = I_m sin ωt, I_m = U_m/r_н при U > 0. (15.1)

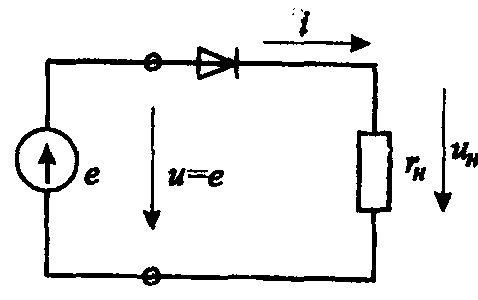
Рис.15.1. Однополупериодный выпрямитель

Постоянная составляющая тока будет равна среднему зна­чению

ω = 2πf = 2π/T, I₀ = I_m/π ≈ 0,32I_m

где ω - частота тока; Т - период колебаний; I_m - ам­плитуда тока.

Действующее значение тока будет

.

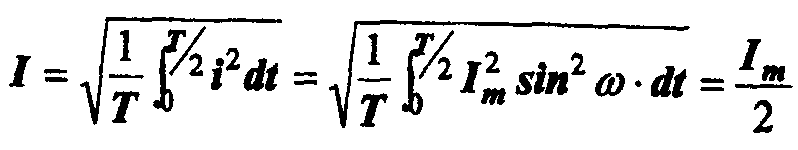Среднее значение напряжения на резисторе r_н при U > 0 равно U₀ = r_нI₀ = (r_нI_m)/π = U_m/π. Коэффициент пульсаций определяется по формуле q = U_m/ U₀.