Решение.
В первой части нам необходимо вычислить методом Гаусса определитель матрицы A. Здесь используется так называемый прямой ход метода Гаусса, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
Для наибольшей точности перестановку строк осуществляют так, чтобы на диагонали оказался максимальный по модулю элемент из каждого столбца.
После проделанных операций вычисляем определитель перемножением диагональных элементов. Результаты приведения матрицы к треугольному виду выглядят следующим образом:
Результаты вычисления определителя занесем в таблицу:
Вычисленное |
Точное (MathCad) |
Погрешность |
4.8125483863 |
4.812548386303 |
2.861710868274*10^-12 |
Во второй части нам необходимо вычислить методом Гаусса обратную матрицу для матрицы A.
Здесь мы используем определение обратной матрицы, т.е. A*A-1=E. Отсюда мы получим пять систем линейных неоднородных уравнений с пятью неизвестными в каждой. Далее каждую систему решим методом Гаусса и, тем самым, определим обратную матрицу.
Полученная обратная матрица:
Эталонная обратная матрица (MathCad) :
В третьей части необходимо вычислить 3 нормы матриц , указанных в пункте 2 настоящего задания:
Результаты занесем в таблицу:
Вид нормы |
А |
А-1 |
m - норма |
71.6022304192 |
9.90563454425 |
l - норма |
145.375383685 |
5.815 |
k - норма |
77.1726220988 |
7.65142110107 |
Вывод: В первых двух частях лабораторной работы мы смогли убедиться в том, что не зря метод Гаусса считается наиболее предпочтительным методом решения систем линейных уравнений, а за одно, и вычисления определителей. Он достаточно прост в применении, но при этом даёт хорошие результаты. Во второй части мы увидели какие значения принимают различные виды норм.
Задание №12
Решение систем линейных уравнений /5,9,19,21,23/.
1. Решить методом Гаусса систему линейных
уравнений
.
Матрица_A:
Вектор правой части b:
Положим параметр a=0.02010+0.002010*N.
2. Решить
систему уравнений
методом простой итерации и методом
Зейделя с точностью
.
Сравнить полученные числа итераций.
Матрица A:
Матрица_b:
Положим параметр a=0.02010+0.001*N.
Решение.
В первой части нам необходимо решить систему линейных уравнений методом Гаусса.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
Для увеличения точности вычислений перестановку строк осуществляют таким образом, чтобы на диаганали оказались элементы, максимальные по модулю среди элементов каждого столбца. Такой метод называется методом Гаусса с выбором главного элемента.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Полученные результаты занесем в таблицу:
Вычисленное |
Эталонное (MathCAD) |
Погрешность |
0.0821306540225 |
0.0821306540176 |
-4.9e-12 |
0.00756671633378 |
0.00756671633355 |
-2.3e-13 |
3.22014156675 |
3.22014156675 |
0 |
-4.18999450688 |
-4.18999450688 |
0 |
-7.10999933305 |
-7.10999933305 |
0 |
Det(A)=0.052926669027234388502
Во второй части нам необходимо решить систему уравнений методом простой итерации и методом Зейделя с точностью .
В методе простых итераций система приводится к виду
и запись итерационного процесса имеет вид
Очевидно,
и
Поэтому
итерации будут заведомо сходиться (и
независимо от начального приближения),
если
.
Приведение к нужному виду можно осуществить по-разному, например, выделить диагональные элементы:
.
В
этой записи легко учесть специальную
структуру матрицы
,
суммируя лишь ненулевые элементы. При
использовании различных норм условия
сходимости имеют вид
которые
означают диагональное преобладание в
матрице. Если метод сходится, то корень
существует и единственный; поэтому
диагональное преобладание, гарантирующее
сходимость, означает что
.
Метод Зейделя отличается тем, что в правой части часть неизвестных берется уже с новой итерации; в этом случае имеем
.
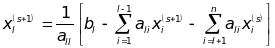Применим метод простых итераций. Исходная матрица имеет вид:
Затем приводим матрицу к виду
Вычисляем Эвклидову норму матрицы α:
||α||= 0.738498806145<1. Это позволяет утверждать,
что метод итераций будет сходиться
независимо от начального приближения
решения и членов правой части. В качестве
начального приближения используем
матрицу
.
Выполняем восемь итераций до тех пор, пока разность результатов между итерациями не будет меньше . Полученные результаты занесем в таблицу:
Вычисленное |
Эталонное (MathCAD) |
Погрешность |
0.072325429545 |
0.0723 |
2.542954532128e-5 |
1.140013632967 |
1.14 |
1.363296695844e-5 |
2.219879330635 |
2.22 |
1.206693648483e-4 |
4.189785907504 |
4.19 |
2.140924964786e-4 |
7.11004841607 |
7.11 |
4.841606992834e-5 |
Применим метод Зейделя. Данный метод аналогичен методу простых итераций, таким же образом выполним условие диагонального преобладания. Выполняем итерационный процесс вида:
Выполним четыре итерации, пока разность результатов между итерациями не будет меньше . Полученные результаты занесем в таблицу:
Вычисленное |
Эталонное (MathCAD) |
Погрешность |
0.072301585857 |
0.0723 |
1.585857490244e-6 |
1.139998795167 |
1.14 |
1.204833209423e-6 |
2.219998525989 |
2.22 |
1.474010892455e-6 |
4.189999721869 |
4.19 |
2.781307051336e-7 |
7.110000286857 |
7.11 |
2.868574426884e-7 |
Вывод: В первой части мы убедились, что метод Гаусса прекрасно подходит для решения систем линейных уравнений. Наряду с небольшим (порядка n3) количеством операций он дает прекрасную точность. Во второй части мы познакомились с итерационными методами простых итераций и Зейделя. Метод Зейделя, как и в большинстве случаев, дал более быструю сходимость, чем метод простых итераций.
Задание №13
Проблема собственных значений и векторов /5,13,17,19/.
1. Найти собственные значения матрицы
методом вращения с точностью
.
Элементы матрицы
представляются в виде многочлена от
параметра
по схеме Горнера следующим образом:
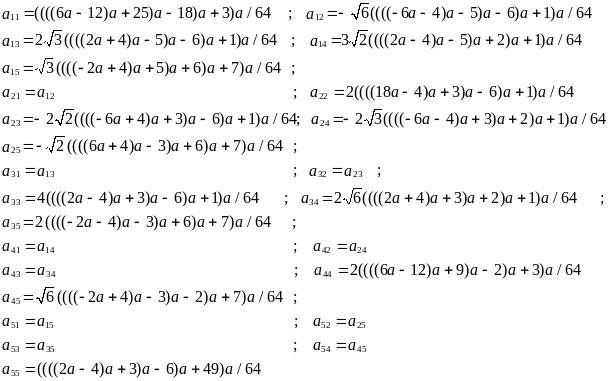
Положим параметр
.
2. Используя найденные собственные значения матрицы из 1 пункта настоящего задания найти методом обратных итераций с точностью собственные вектора этой матрицы .
3. Используя
вычисленные собственные значения
матрицы
,
вычислить число обусловленности
матрицы
(
=
?).
4. Найти
методом Данилевского собственные
значения матрицы
с точностью
.
Элементы исходной матрицы имеют вид:
Положим
параметр
.
Решение.
Метод вращений Якоби применим только
для симметрических матриц
(
)
и решает полную проблему собственных
значений и собственных векторов таких
матриц. Он основан на отыскании с помощью
итерационных процедур матрицы
в преобразовании подобия
,
а поскольку для симметрических матриц
матрица преобразования подобия
является ортогональной (
),
то
,
где
- диагональная матрица с собственными
значениями на главной диагонали
.
Пусть дана симметрическая матрица A.
Требуется для нее вычислить с точностью
все собственные значения и соответствующие
им собственные векторы. Алгоритм метода
вращения следующий:
Пусть известна
матрица
на k–й итерации,
при этом для k=0
.
1. Выбирается
максимальный по модулю недиагональный
элемент
матрицы
(
=
)
.
2. Ставится
задача найти такую ортогональную матрицу
,
чтобы в результате преобразования
подобия
произошло обнуление элемента
матрицы
.
В качестве ортогональной матрицы
выбирается матрица вращения, имеющая
следующий вид:
,
В матрице
вращения на пересечении
й
строки и
го
столбца находится элемент
где
-
угол вращения, подлежащий определению.
Симметрично относительно главной
диагонали (
-я
строка,
-й
столбец) расположен элемент
;
Диагональные элементы
и
равны соответственно
,
;
другие диагональные элементы
остальные
элементы в матрице вращения
равны нулю.
Угол вращения
определяется из условия
:
причем если
то
.
3. Строится матрица
в которой
элемент
В качестве критерия окончания итерационного процесса используется условие малости суммы квадратов внедиагональных элементов:
Если
то итерационный процесс
продолжается.
Если
,
то итерационный процесс останавливается,
и в качестве искомых собственных значений
принимаются
.
Координатными столбцами собственных
векторов матрицы
в единичном базисе будут столбцы матрицы
т.е.
причем эти
собственные векторы будут ортогональны
между собой, т.е.
Исходная матрица имеет следующий вид:
Полученная после 15-ти вращений матрица имеет следующий вид:
При этом количестве итераций выполняется условие прекращения вращения:
Полученные результаты занесем в таблицу:
Полученное |
Эталонное (MathCAD) |
Погрешность |
0.280999952636 |
0.281 |
4.736399999983e-8 |
-0.078958361275 |
-0.078961 |
2.638725000004e-6 |
0.022182805315 |
0.022188041 |
5.235684999997e-6 |
0.001754584465 |
0.001751989905 |
2.59456e-6 |
-0.006234789758 |
-0.006234839521 |
4.976300000022e-8 |
Во второй части работы необходимо,
используя найденные собственные значения
матрицы
из 1 пункта настоящего задания, найти
методом обратных итераций с точностью
собственные вектора этой матрицы
.
Фиксируем любое
.
Итерации организуются по формуле:
Полученные результаты занесем в таблицу:
|
|
|
|
|
1.07935034e-5 |
4.54965069e-3 |
0.99991608 |
-0.01248089 |
-1.16694021e-4 |
1.42079542e-4 |
-2.58813769e-3 |
0.012112 |
0.99991838 |
9.79930689e-4 |
-4.75196789e-6 |
0.9999863 |
-4.59567838e-3 |
2.64500817e-3 |
4.19817054e-6 |
3.80739074e-4 |
-3.66757701e-5 |
-7.98253381e-5 |
-6.59029209e-4 |
0.99999944 |
0.99999992 |
-2.36708089e-6 |
7.39370405e-6 |
-1.51236616e-4 |
-3.81214985e-4 |
Эталонные (MathCAD) значения занесем в следующую таблицу:
|
|
|
|
|
1.097634e-5 |
4.57548525e-3 |
0.99991324 |
-0.01235163 |
-1.15009748e-4 |
1.42249301e-4 |
-2.55550819e-3 |
0.01236351 |
0.99991981 |
9.8611319e-4 |
-4.62059301e-6 |
0.99998627 |
-4.54355551e-3 |
2.61185404e-3 |
3.52096423e-6 |
3.80903817e-4 |
-4.72790336e-7 |
1.02819128e-4 |
-9.87518422e-4 |
0.99999943 |
0.99999992 |
4.93400723e-6 |
-1.27942479e-5 |
-1.41714112e-4 |
-3.81042629e-4 |
Погрешность вычислений занесем в следующую таблицу:
|
|
|
|
|
-1.82836609e-7 |
-2.58345545e-5 |
2.84222094e-6 |
-1.29262956e-4 |
-1.68427297e-6 |
-1.69758517e-7 |
-3.26294924e-5 |
-2.51517186e-4 |
-1.42317868e-6 |
-6.1825005e-6 |
-1.31374879e-7 |
3.329175e-8 |
-5.21228716e-5 |
3.31541296e-5 |
6.77206303e-7 |
-1.64743218e-7 |
-3.62029797e-5 |
-1.82644466e-4 |
3.28489213e-4 |
5.81377346e-9 |
8.80368001e-11 |
-7.30108811e-6 |
2.01879519e-5 |
-9.52250429e-6 |
-1.72355846e-7 |
В третьей части задания необходимо используя вычисленные собственные значения матрицы , вычислить число обусловленности матрицы ( = ?).
Для симметричных матриц число обусловленности матрицы A равно отношению максимального собственного числа к минимальному числу. Пользуясь этим определением и ранее полученными данными определяем данное отношение:
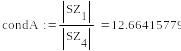
В четвертой части задания нужно найти методом Данилевского собственные значения матрицы с точностью .
Для этого всего лишь на всего нам нужно привести нашу исходную матрицу к нормальному виду Фробениуса. Матрица Фробениуса имеет вид:
Согласно методу Данилевского переход
от матрицы
к ей подобной матрице
осуществляется с помощью
преобразований подобия, последовательно
преобразующих строки матрицы
,
начиная с последней.
Исходная матрица имеет вид:
Приведенная к нормальной форме Фробениуса матрица имеет вид:
Отсюда мы получаем формулу для характеристического многочлена:
Находим корни данного многочлена, результаты заносим в таблицу:
Полученное |
Эталонное (MathCAD) |
Погрешность |
0.141000000051 |
0.140999924226 |
7.5825e-8 |
0.0409999999891 |
0.041000013222 |
1.32329e-8 |
0.34100000016 |
0.340999779445 |
2.20715e-7 |
0.440999999802 |
0.441000207517 |
2.07715e-7 |
0.240999999888 |
0.241000176759 |
1.76871e-7 |
0.48200000011 |
0.48199989883 |
1.0128e-7 |
Вывод:
Метод вращения Якоби очень удобен, но существенным недостатком является то, что он применим только для симметричных матриц. Немаловажным является и тот факт, что при подсчетах иногда приходится работать с очень большими матрицами.
Метод обратных итераций дает хорошую точность уже после одной итерации с использованием значений, которые мы изначально получили с какой-то погрешностью.
Число обусловленности имеет большое значение для определении устойчивости решения системы линейных уравнений, определяемых данной матрицей, при изменении начальных данных.
Метод Данилевского относительно простой и универсальный метод. Минус метода заключается в том, что, при нахождении собственных значений, необходимо привлекать дополнительный математический аппарат, поскольку метод дает лишь многочлен для определения собственных значений.
Задание № 14
Интегрирование обыкновенных дифференциальных уравнений с помощью степенных рядов и методом Пикара /10,15,16,22/ .
1. Написать 7 членов разложения в степенной
ряд решения
дифференциального уравнения Эйлера:
,
N – натуральное число.
Решение уравнения должно удовлетворять начальным условиям:
Пользуясь
полученным разложением, найти значения
приближенного решения дифференциального
уравнения в точках
для
и сравнить полученные значения с точными
значениями решения в этих же точках.
2. Написать 6 членов разложения в степенной ряд решения дифференциального уравнения:
Решение уравнения должно удовлетворять начальным условиям:
.
Пользуясь
полученным разложением, найти значения
приближенного решения в точках
для
и сравнить полученные значения с точными
значениями решения в этих же точках.
3. Проинтегрировать методом Пикара систему дифференциальных уравнений:
с точностью
на интервале
с шагом
.
Решение системы должно удовлетворять следующим начальным условиям:
;
.
Определить формулу вычисления первого приближения и обосновать ее. Показать число итераций, которое было получено при достижении заданной точности.
Решение.
Разложение дифференциального уравнения в степенной ряд выглядит следующим образом:
,где
.
В нашем случае:
,где
.
Как видно, для разложения в ряд нам потребуется производные до 6-го порядка включительно, вычислим их последовательно из нашего уравнения:
- исходное уравнение.
Введем обозначения:
.
Тогда уравнение можно преобразовать к
виду:
,
тогда:
Используя начальные данные для численного вычисления производных, получим значения коэффициентов разложения:
i |
Ci |
0 |
2 |
1 |
4 |
2 |
-1.12275 |
3 |
1.6455 |
4 |
0.1681875 |
5 |
-95.833125 |
6 |
-4.5007396875*10^4 |
Точное значение вычислено с помощью программы Maplesoft Maple 12. Это сделано из-за достаточного просто построения, как общего, так и частного решения ОДУ в данной программе.
Полученные результаты заносим в таблицу:
xi |
Вычисленное значение |
Точное значение (Maple 12) |
Погрешность |
2 |
2 |
2 |
0 |
2.01 |
2.039889317591 |
2.039887764037 |
-1.553554368705e-6 |
2.02 |
2.079560903771 |
2.079551220275 |
-9.683495198143e-6 |
2.03 |
2.118998950595 |
2.118990632489 |
-8.318105762406e-6 |
2.04 |
2.15811517895 |
2.158206287235 |
9.110828497461e-5 |
2.05 |
2.196666675244 |
2.19719849306 |
5.31817815554e-4 |
2.06 |
2.234141322763 |
2.235967579719 |
1.826256955463e-3 |
2.07 |
2.269610827714 |
2.274513897432 |
4.903069718075e-3 |
2.08 |
2.30155133993 |
2.312837816152 |
0.011286476222 |
2.09 |
2.327631668259 |
2.350939724862 |
0.023308056602 |
2.10 |
2.344469090625 |
2.388820030889 |
0.044350940264 |
2.11 |
2.347352758755 |
2.426479159244 |
0.079126400489 |
График решения выглядит следующим образом:
Вторую часть выполняем аналогично первой.
В нашем случае:
,где
.
Вычисляя недостающие производные из начального уравнения и, используя начальные данные для численного вычисления производных, получим значения коэффициентов разложения:
i |
Ci |
0 |
0.333333333333 |
1 |
-0.333333333333 |
2 |
0.172027290448 |
3 |
-0.14768940657 |
4 |
0.169661389459 |
5 |
-0.190001288564 |
Полученные результаты заносим в таблицу:
xi |
Вычисленное значение |
Точное значение (Maple 12) |
Погрешность |
2.021 |
0.326407861837 |
0.326430311535 |
2.244969853743e-5 |
2.031 |
0.323161069657 |
0.323210279638 |
4.92099810116e-5 |
2.041 |
0.31994612305 |
0.320032668935 |
8.654588481466e-5 |
2.051 |
0.316762267406 |
0.31689684469 |
1.345772833291e-4 |
2.061 |
0.313608779489 |
0.313802180988 |
1.934014991158e-4 |
2.071 |
0.31048496515 |
0.310748060699 |
2.630955492128e-4 |
2.081 |
0.307390157053 |
0.307733875437 |
3.437183843128e-4 |
2.091 |
0.304323712392 |
0.304759025515 |
4.35313122277e-4 |
2.101 |
0.301285010613 |
0.301822919889 |
5.379092764197e-4 |
2.111 |
0.298273451129 |
0.298924976108 |
6.51524978972e-4 |
График решения выглядит следующим образом:
В третьей части необходимо проинтегрировать систему методом Пикара.
Запишем
систему в общем виде:
.
Тогда итерационный процесс будет выглядеть следующим образом:
Процесс продолжаем до того момента, когда разность между итерациями будет меньше заданной погрешности.
Полученные результаты нанесем в таблицу:
xi |
y1 |
y2 |
y3 |
0.64 |
-0.483712 |
0.316288 |
-2.083712 |
0.65 |
-0.49760666 |
0.30847565 |
-2.11010431 |
0.66 |
-0.51168727 |
0.30015451 |
-2.13666899 |
0.67 |
-0.52597241 |
0.29132419 |
-2.16341238 |
0.68 |
-0.54048021 |
0.28198386 |
-2.19034178 |
0.69 |
-0.55522844 |
0.27213222 |
-2.21746534 |
0.7 |
-0.57023453 |
0.26176745 |
-2.24479202 |
0.71 |
-0.58551564 |
0.2508872 |
-2.27233157 |
0.72 |
-0.60108871 |
0.23948851 |
-2.30009443 |
0.73 |
-0.61697054 |
0.22756782 |
-2.32809178 |
0.74 |
-0.63317781 |
0.21512094 |
-2.35633542 |
0.75 |
-0.64972714 |
0.20214303 |
-2.38483783 |
0.76 |
-0.66663518 |
0.18862862 |
-2.41361208 |
0.77 |
-0.68391858 |
0.17457154 |
-2.44267185 |
0.78 |
-0.70159412 |
0.15996499 |
-2.47203142 |
0.79 |
-0.71967871 |
0.14480146 |
-2.50170564 |
0.8 |
-0.73818941 |
0.1290728 |
-2.53170992 |
0.81 |
-0.75714351 |
0.1127702 |
-2.56206025 |
В следующую таблицу занесем погрешности между 6-й и 7-й итерацией:
xi |
Погрешность y1 |
Погрешность y2 |
Погрешность y3 |
0.64 |
0 |
0 |
0 |
0.65 |
-1.91346938e-13 |
-1.02862163e-13 |
-3.63709063e-13 |
0.66 |
-2.33294495e-11 |
-1.23137611e-11 |
-4.42295089e-11 |
0.67 |
-3.7997494e-10 |
-1.96958783e-10 |
-7.18648696e-10 |
0.68 |
-2.71512945e-9 |
-1.38216411e-9 |
-5.12300113e-9 |
0.69 |
-1.23557851e-8 |
-6.17734058e-9 |
-2.32591755e-8 |
0.7 |
-4.22754037e-8 |
-2.07583321e-8 |
-7.93997281e-8 |
0.71 |
-1.18822026e-7 |
-5.73039355e-8 |
-2.22665104e-7 |
0.72 |
-2.8923405e-7 |
-1.37002042e-7 |
-5.40810039e-7 |
0.73 |
-6.30881105e-7 |
-2.93508455e-7 |
-1.17706012e-6 |
0.74 |
-1.26210837e-6 |
-5.76724791e-7 |
-2.34973446e-6 |
0.75 |
-2.35452455e-6 |
-1.05675803e-6 |
-4.37432603e-6 |
0.76 |
-4.14655132e-6 |
-1.827929e-6 |
-7.68767656e-6 |
0.77 |
-6.95804136e-6 |
-3.01270719e-6 |
-1.28738705e-5 |
0.78 |
-1.12057701e-5 |
-4.7654629e-6 |
-2.06914754e-5 |
0.79 |
-1.74196101e-5 |
-7.27594232e-6 |
-3.21017698e-5 |
0.8 |
-2.62592059e-5 |
-1.07723871e-5 |
-4.82976216e-5 |
0.81 |
-3.85309782e-5 |
-1.5524235e-5 |
-7.07327049e-5 |
Вывод: метод степенных рядов для решения ОДУ достаточно прост, но в более сложных задачах могут возникнуть проблемы с точностью при вычислении нужных производных. Метод последовательных приближений оказался несколько более сложным, но он позволяет вычислить дифференциальное уравнение или систему с заданной точностью.
Задание № 15