Решение.

В первой части нам необходимо вычислить действительные корни алгебраического уравнения посредством метода итераций. Выпишем левую часть уравнения и построим ее график:

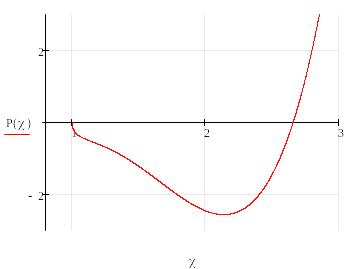
Из графика видно, что вещественных корня – два, причём x₁ [0.9;1.1] и x₂ [2.5;2.8].

Вычислим эталонные (MathCad) значения этих корней:

i	Xi
0	1.0
1	2.6590534252

Суть метода итераций заключается в приведении заданного уравнения к виду x=f(x), определении начального приближения корня и последующем его уточнении посредством выполнения итераций x_n=f(x_n-1).

Из теории можно заключить, что если функция f(x) определена и дифференцируема на отрезке [a;b], причём все её значения f(x) [a;b]. Тогда, если существует правильная дробь q такая, что при , то

1. Процесс итерации x_n=f(x_n-1) сходиться независимо от начального значения x₀ [a;b].

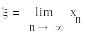2. - является единственным корнем уравнения x=f(x).

Производная левой части нашего уравнения определяется следующим выражением:

Из этой формулы легко видеть, что , поэтому не выполнены требования теории и, следовательно, вычислить корень x=1.0 методом итераций невозможно.

Для другого корня все условия выполняются. Итерации будем производить до тех пор, пока разность между итерациями не будет меньше

_{В качестве начального приближения берем}

Результаты занесем в таблицу:

№ - итерации	Эталон (MathCad)	Вычисленное	Погрешность
1	2.6590534252	2.658629014343	4.24410856656*10^-4
2	2.6590534252	2.659038543854	1.488134572503*10^-5
3	2.6590534252	2.659052911787	5.134129268392*10^-7

Во второй части нам необходимо вычислить корни многочлена посредством метода Бернулли. График левой части уравнения выглядит следующим образом:

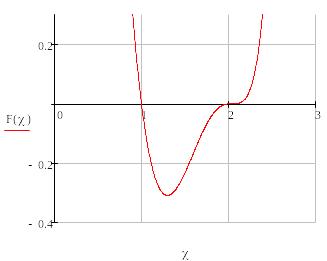
Для того чтобы более точно понять как нам действовать, вычислим корни – эталоны с помощью MathCad. Результаты занесем в таблицу:

№	x
1	1.0
2	2.05
3	2.05
4	2.05
5	0.5-1.3416407865i
6	0.5+1.3416407865i

Из таблицы можно увидеть, что у нас 4 действительных корня, один кратности 3, а другой кратности 1. Комплексных корня у нас 2.

Согласно методу Бернулли, начальное уравнение:

_{Заменяем конечно–разностным уравнением:}

Причём первые значения определим следующим образом:

Согласно теории корень будем искать по формуле:

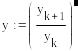
Учитывая всё вышеизложенное, мы в состоянии вычислить корень. Для достижения необходимой точности было проведено приблизительно 45000 итераций. Результаты заносим в таблицу:

Эталон (MathCad)	Вычисленное	Погрешность	F(x0)
2.05	2.050094815812	9.481581199999*10^-5	3.861799768856*10^-12

Далее разделим исходный многочлен (1) на скобку (x+2.05)³, в результате данный корень будет исключён. Многочлен теперь будет определяться выражением:

Следующие превалирующие корни комплексно-сопряженные. Здесь все рассуждения полностью аналогичны вышеописанным, единственным же существенным отличием, является то, что рассматриваются последовательности вида:

здесь r – модуль комплексного корня; u – действительная часть; v – мнимая часть;

Учитывая всё вышеизложенное, мы в состоянии вычислить комплексные корни. Производим 200 итераций. Результаты заносим в таблицу:

Эталон (MathCad)	Вычисленное	Погрешность	F(x0)
0.5-1.3416407865i	0.5-1.3416407865i	0	4.110489726372*10^-12-8.668621376273i*10^-13
0.5+1.3416407865i	0.5+1.3416407865i	0	4.110489726372*10^-12+8.668621376273i*10^-13

Далее разделим многочлен на скобку, определяемую этими комплексно-сопряжёнными корнями, в результате данные корни будут исключены. Многочлен теперь будет определяться простейшим выражением

Отсюда, естественно и тривиально, определяем последний корень.

Вывод: мы исследовали два метода решения алгебраических нелинейных уравнений. Метод итераций оказался довольно быстрым и удобным методом, на количество итераций, во многом, влияет начальное приближение. Метод Бернулли тоже очень действенный, позволяет найти все корни уравнения, не зависимо от начального приближения, с большой точностью. Единственным требованием для метода Бернулли является лишь отдаленность корней.

Задание №11

Алгебра матриц. Вычисление определителей, обратных матриц, норм матриц /5,9,19/.

1. Вычислить методом Гаусса определитель матрицы A:

Положим параметр .

2. Вычислить методом Гаусса обратную матрицу для матрицы A:

Положим параметр .

3. Вычислить 3 нормы матриц , указанных в пункте 2 настоящего задания:

а) - норма

б) - норма

в) - норма.