Решение.
Будем использовать метод Греффе-Лобачевского для решения алгебраического уравнения вида
.
Предположим, что корни этого уравнения
действительны и различны по абсолютной
величине. Расположим их в порядке
убывания корней:
.
Составим
уравнение, корнями которого являются
(k=1,2,…,n).
Оно будет иметь вид
, где
,
,
,
,
………………………………..
.
Процесс перехода от корней
к корням
называется квадрированием корней.
Квадрирование следует остановить тогда, когда коэффициенты нового преобразованного уравнения будут представлять собой, в пределах заданной точности, квадраты соответствующих коэффициентов последующего преобразованного уравнения за счет отсутствия удвоенных произведений.
Абсолютные
величины корней находим по формулам
,
.
Подстановкой в данное уравнение
определяем знаки корней.
Результаты квадрирования по каждой итерации:
i |
A1 |
A2 |
A3 |
A4 |
0 |
1 |
1.89 |
-2.3531 |
-1.524735 |
1 |
1 |
8.2783 |
16.63934181 |
9.9310260823 |
2 |
1 |
35.25156727 |
117.437103791 |
20.241623911 |
3 |
1 |
1.0077987874e3 |
1.2366411331e4 |
171.7825607794 |
4 |
1 |
9.9092557324e5 |
1.5258188547e8 |
1.9829299617e4 |
5 |
1 |
9.8162832793e11 |
2.3281192474e16 |
3.5967119225e8 |
6 |
1 |
9.6359412764e23 |
5.4201392303e32 |
1.2882587293e17 |
7 |
1 |
9.2851364283e47 |
2.9377909276e65 |
1.6595961222e34 |
i |
A5 |
A6 |
A7 |
A8 |
0 |
2.66938195 |
-1.1938358457 |
0.2218682871 |
-0.0147725693 |
1 |
2.4967171777 |
0.2857901316 |
0.0139534913 |
2.1822880412e-4 |
2 |
1.017958859 |
0.0163346285 |
6.9964641458e-5 |
4.7623810946e-8 |
3 |
0.3913909579 |
1.263058009e-4 |
3.3392165373e-9 |
2.2680273691e-15 |
4 |
0.1098752023 |
1.3340056238e-8 |
0 |
0 |
5 |
0.0115435154 |
0 |
0 |
0 |
6 |
1.3312640704e-4 |
0 |
0 |
0 |
7 |
1.7722632304e-8 |
0 |
0 |
0 |
Останавливаемся на седьмой итерации, поскольку, как мы увидим далее, такого количества вполне достаточно для достижения необходимой точности.
Таким образом, получаем:
Xi |
Точное значение |
Полученное |
Погрешность |
1 |
0.27 |
0.27 |
7.3721584393*10^-12 |
2 |
0.57 |
0.57 |
3.8722751117*10^-8 |
3 |
-2.37 |
2.37 |
0 |
4 |
0.17 |
0.17 |
0 |
5 |
-1.37 |
1.37 |
0 |
6 |
0.37 |
0.37 |
2.2204460493*10^-15 |
7 |
0.47 |
0.47 |
7.1276318181*10^-14 |
Второй пункт задания абсолютно аналогичен первому.
Результаты квадрирования по каждой итерации:
i |
A0 |
A1 |
A2 |
A3 |
0 |
1 |
-4.2 |
5.55837192 |
-4.532581032 |
1 |
1 |
6.52325616 |
1.9511024048 |
-27.4185289255 |
2 |
1 |
38.6506661194 |
397.3045066465 |
682.65845597 |
3 |
1 |
699.2649781838 |
1.05726475e5 |
2.0935915507e5 |
4 |
1 |
2.7751855971e5 |
1.0885501129e10 |
2.1770169706e10 |
5 |
1 |
5.5245548724e10 |
1.1848205159e20 |
2.3696410302e20 |
6 |
1 |
2.8151065507e21 |
1.4037996523e40 |
2.8075993046e40 |
7 |
1 |
7.8967488985e42 |
1.9706534638e80 |
3.9413069276e80 |
i |
A4 |
A5 |
A6 |
0 |
4.5646423363 |
-0.332581032 |
6.2704162611e-3 |
1 |
17.8907653148 |
0.0533657278 |
3.9318120088*10^-5 |
2 |
323.0060564798 |
1.4410383836e-3 |
1.5459145672*10^-9 |
3 |
1.0433094505e5 |
1.077912087e-6 |
0 |
4 |
1.0884946095e10 |
6.6322346339e-13 |
0 |
5 |
1.1848205148e20 |
0 |
0 |
6 |
1.4037996523e40 |
0 |
0 |
7 |
1.9706534638e80 |
0 |
0 |
Останавливаемся на седьмой итерации, поскольку, как мы увидим далее, такого количества вполне достаточно для достижения необходимой точности.
Видим, что A3 меняет знак, что характерно для комплексного корня. Найдем эти корни.
Квадрат модуля комплексно-сопряжённых чисел определяется равенством:
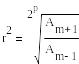
Am в данном случае – коэффициент, меняющий в ходе итераций свой знак.
Для вычисления мнимой и действительной частей комплексных чисел необходимо воспользоваться формулами:
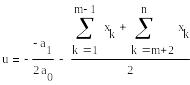
Таким образом, получаем:
Xi |
Точное значение |
Полученное |
Погрешность |
1 |
2.1633974045 |
2.163397458 |
5.3412390066*10^-8 |
2 |
0.0366025955 |
0.0366025945 |
9.0368602879*10^-10 |
3 |
0.0404094415 |
0.0404094425 |
9.9767375611*10^-10 |
4 |
1.9595905585 |
1.9595905101 |
4.8380576434*10^-8 |
5 |
-1i |
2.5629005584*10^-9-1i |
2.5629005584*10^-9 |
6 |
1i |
2.5629005584*10^-9+1i |
2.5629005584*10^-9 |
Рассмотрим последний пункт.
Поступаем так же, как и в двух предыдущих пунктах. Результаты квадрирования по каждой итерации заносим в следующую таблицу:
i |
A0 |
A1 |
A2 |
A3 |
0 |
1 |
1.8192 |
-1.73222784 |
-4.29311296 |
1 |
1 |
6.77394432 |
18.321904028 |
25.1322729491 |
2 |
1 |
9.2425135945 |
31.7429400233 |
49.863906714 |
3 |
1 |
21.938177498 |
157.0438510712 |
404.5530833338 |
4 |
1 |
167.1959297918 |
7.624825372e3 |
5.3187003136e4 |
5 |
1 |
1.2704828195e4 |
4.0555291774e7 |
1.2839938196e9 |
6 |
1 |
8.0302075917e7 |
1.6121262768e15 |
8.2019050757e17 |
i |
A4 |
A5 |
A6 |
0 |
-0.1493857277 |
2.5146800438 |
0.9652087885 |
1 |
18.270003999 |
6.6119925573 |
0.9316280053 |
2 |
35.5826405522 |
9.6767508128 |
0.8679307403 |
3 |
356.1844558916 |
31.87297118 |
0.75330377 |
4 |
1.0131535254e5 |
479.2561049963 |
0.5674665698 |
5 |
1.0213828921e10 |
1.1470026303e5 |
0.3220183079 |
6 |
1.0432200669e20 |
6.5780705259e9 |
0.5674665698 |
Останавливаемся на шестой итерации. Такого количества итераций достаточно, чтобы достичь нужной точности.
В данном пункте мы рассматриваем случай кратных корней. Это видно в процессе квадрирования (пары x1 и x2, x3 и x4, x5 и x6 сходятся постепенно к одному и тому же значению ). Поэтому для них применимы следующие формулы:
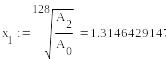
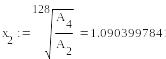
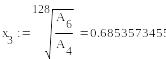
Таким образом, мы получаем:
Xi |
Точное значение |
Полученное |
Погрешность |
1 |
1.0904 |
1.0903997841 |
6.6923133701*10^-11 |
2 |
1.0904 |
1.0903997841 |
6.6923133701*10^-11 |
3 |
-1.3146426545 |
1.3146429147 |
2.1587167409*10^-7 |
4 |
-1.3146426544 |
1.3146429147 |
2.1587167409*10^-7 |
5 |
-0.6853573455 |
0.6853573455 |
6.6923133701*10^-11 |
6 |
-0.6853573456 |
0.6853573455 |
6.6923133701*10^-11 |
Вывод:
Метод Греффе-Лобачевского оказался весьма эффективным для поиска корней многочленов с заданной точностью. Особенно следует отметить то, что для достижения нужной точности необходимо лишь увеличить количество этапов квадрирования. Важным так же является то, что корни мы получаем с точностью до знака, знак же можно определить из простой подстановки.
Задание ¹10
Решение алгебраических нелинейных уравнений. Методы итераций и Бернулли /9,12,19/.
1. Найти методом итераций все корни уравнения:
с точностью
.
Положим
.
2. Решить методом Бернулли уравнение:
с точностью
.
Положим
В данном пункте в ответе показать результаты итерирования (по Бернулли) и способы вычисления корней.