Решение.

Нам требуется вычислить несобственные интегралы с точностью трёх значащих цифр. Значащей цифрой приближенного числа называется всякая цифра в его изо­бра­жении, отличная от 0, и 0, если он содержится между двумя значащими цифрами или является представителем сохраняющегося десятичного разряда. Все остальные нули, входящие в состав числа и служащие для обозначения десятичных разрядов, не причисляются к значащим цифрам.

В задании сказано, что вычисление интегралов следует произвести методом Симпсона, но, как хорошо известно, данный метод применим только на конечном отрезке интегрирования и только для интегралов без особенностей. Поэтому нам нужно свести данные несобственные интегралы к определённым интегралам. Для этого нам нужно определить границы интегрирования для определённых интегралов, отбросив бесконечный предел или особенность таким образом, чтобы интеграл по отбрасываемому интервалу был меньше заданной ошибки вычисления.

Рассмотрим первый интеграл. Для того, чтобы узнать, с какой точностью нам необходимо вычислить этот интеграл, посмотрим на его эталонное значение, вычисленное с помощью MathCAD:

Полученный результат означает, что для того, чтобы получить точность трех значащих цифр, нам необходимо вычислить этот интеграл с точностью ε=10^-4.

График подынтегральной функции выглядит следующим образом:

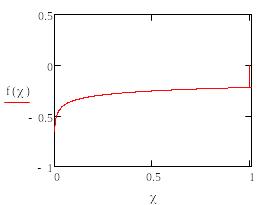
Подынтегральная функция имеет две особенности: x1=0; x2=1.

Разобьем данный интеграл на три:

Выберем и такими, чтобы , .

А собственный интеграл вычислим по формуле Симпсона с точностью .

Для подынтегральной функции сделаем оценку:

По следующему графику можно убедиться, что оценка справедлива:

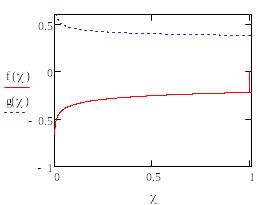
Тогда для a и b получим следующие результаты:

a	b
4.601890830661*10^-6	0.999912373784

Вычисляем определенный интеграл с полученными границами интегрирования с помощью метода Симпсона. Количество разбиений находим по формуле остаточного члена:

Полученные результаты заносим в таблицу:

Полученное	Эталонное(MathCAD)	Погрешность
-0.274234491896	-0.274306311554	7.181965830866*10^-5

Рассмотрим второй интеграл. Для того, чтобы узнать, с какой точностью нам необходимо вычислить этот интеграл, посмотрим на его эталонное значение, вычисленное с помощью MathCAD:

Полученный результат означает, что для того, чтобы получить точность трех значащих цифр, нам необходимо вычислить этот интеграл с точностью ε=3,5*10^-3. Данная точность выбрана с учетом, как особенностей интеграла, так и с учетом возможностей MathCAD.

График подынтегральной функции выглядит следующим образом:

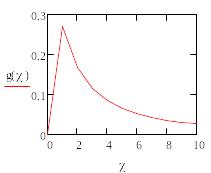
Подынтегральная функция имеет особенность в .

Разобьем интеграл на два: и выберем таким большим, чтобы .

Собственный интеграл вычислим по формуле Симпсона с точностью .

Сделаем оценку интеграла:

В справедливости данной оценки можно убедиться на графике:

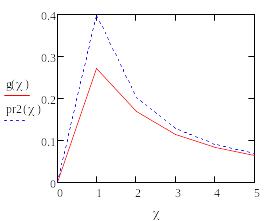
Тогда для b получим следующий результат:

Вычисляем определенный интеграл с полученными границами интегрирования с помощью метода Симпсона. Количество разбиений находим по формуле остаточного члена:

Полученные результаты заносим в таблицу:

Полученное	Эталонное(MathCAD)	Погрешность
1.62346650371	1.625565898585	2.099394875006*10^-3

Рассмотрим третий интеграл.Для того, чтобы узнать, с какой точностью нам необходимо вычислить этот интеграл, посмотрим на его эталонное значение, вычисленное с помощью MathCAD:

График подынтегральной функции выглядит следующим образом:

Этот интеграл имеет две особенности: х = 0, .

Разобьем интеграл на три: . Выберем и такими, чтобы , .

Определенный интеграл вычислим по формуле Симпсона с точностью .

Для интегралов с особенностями получаем оценки:

Отсюда для a и b получаем:

a	b
8.519048592653*10^-6	2.610347628962

Вычисляем определенный интеграл с полученными границами интегрирования с помощью метода Симпсона. Количество разбиений находим по формуле остаточного члена:

Полученные результаты заносим в таблицу:

Полученное	Эталонное(MathCAD)	Погрешность
0.320007840676	0.320341603946	3.337632708473*10^-4

Вывод: Вычисление несобственных интегралов является достаточно сложным и долгим процессом, особенно на стадии подбора границ интегрирования. Но, несмотря на все минусы, рассмотренный метод позволил вычислить заданные интегралы с нужной точностью.

Задание ¹9

Решение алгебраических уравнений методом Греффе-Лобачевского.

1.Найти корни многочлена методом Греффе-Лобачевского с точностью :

а)

б)

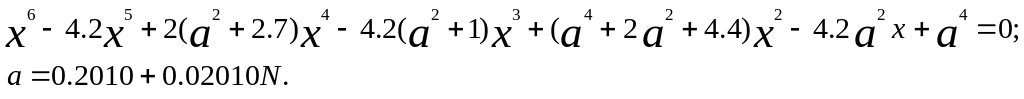
в)

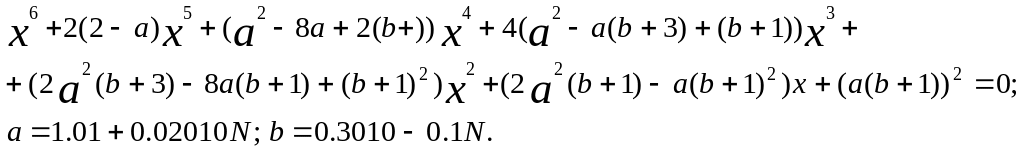
В результате этой работы необходимо показать, как получен каждый корень: то есть привести результаты квадрирования по каждой итерации и так далее.