Решение.

Формулами Ньютона-Котеса называются формулы численного интегрирования, в которых заранее определенные узлы отстоят на равном расстоянии h друг от друга, и концы отрезка интегрирования обязательно входят в число узлов. Формулы Ньютона-Котеса бывают различных порядков, в зависимости от количества узлов, которое используется при интегрировании на элементарном отрезке. Формула n-го порядка получается путем построения многочлена Лагранжа в n+1 точке. Затем полученный полином интегрируется от x_i-1 до x_i и, суммируя такие интегралы по отрезку [a,b], получим для каждого значения n соответствующую квадратурную формулу для вычисления интеграла. Выпишем эти формулы вместе с остаточными членами:

При n=2 получаем формулу трапеций:

= ;

При n=3 получаем формула Симпсона (только для чётных значений m):

; При n=4 получаем формулу:

При n=5 получаем формулу:

Теперь приступим к первой части задания. Рассмотрим первый интеграл.

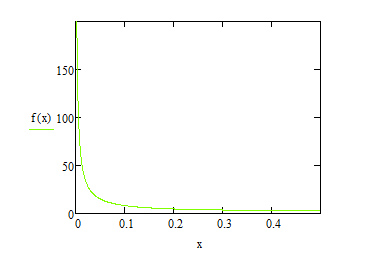
Из графика видно, что подынтегральная функция имеет особенность в точке x=0. Чтобы избавится от этой особенности, применим известную формулу интегрирования по частям.

Число разбиений отрезка интегрирования берем равным 20, получаем таблицу:

Метод	Полученное	Эталон (MathCad)	Погрешность
Трапеций	10.48849540364	10.492377155975	3.881752334651*10^-3
Симпсона	10.492302809241	10.492377155975	7.434673428364*10^-5
Н-К (n=4)	10.492273009857	10.492377155975	1.041461177813*10^-4
Н-К (n=5)	10.492325051818	10.492377155975	5.210415668699*10^-5

Далее рассмотрим второй интеграл:

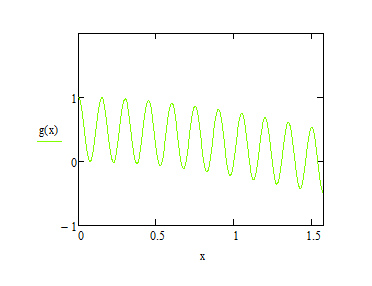
Подынтегральная функция не имеет особенностей. Число разбиений отрезка интегрирования берем равным 20, получаем таблицу:

Метод	Полученное	Эталон (MathCad)	Погрешность
Трапеций	0.499742952624	0.5	2.57047375734*10^-4
Симпсона	0.500000105773	0.5	1.057732950116*10^-7
Н-К (n=4)	0.52618524836	0.5	2.618524836042*10^-2
Н-К (n=5)	0.499999999751	0.5	2.491820083605*10^-10

Теперь приступим ко второй части задания. Нам необходимо вычислить 2 интеграла по формулам трапеций и Симпсона с точностью , определяя шаг интегрирования по оценке остаточного члена. Выпишем остаточные члены для каждой из формул интегрирования:

Для метода трапеций:

Для метода Симпсона:

Выразим h из этих формул:

Для метода трапеций: ,

Для метода Симпсона: ,

Рассмотрим первый интеграл:

Для избавления от особенности в нуле заменим левую границу интегрирования на 10^-4. Для выбора точки минимизируем соответствующие производные:

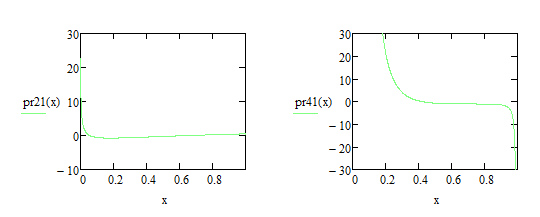
Для метода Трапеций получаем шаг h=0.04 Количество разбиений Nraz=25

Для метода Симпсона получаем шаг h=0.125 Количество разбиений Nraz=8

Результаты интегрирования занесем в таблицу:

Метод	Полученное	Эталон (MathCad)	Погрешность
Трапеций	0.020323124864	0.020330958472	7.833608312947*10^-6
Симпсона	0.020412811678	0.020330958472	8.185320605485*10^-5

Рассмотрим второй интеграл:

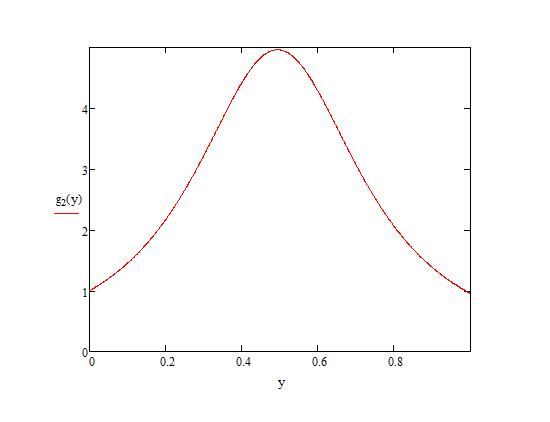
Подынтегральная функция не имеет особенностей. Для выбора точки минимизируем соответствующие производные:

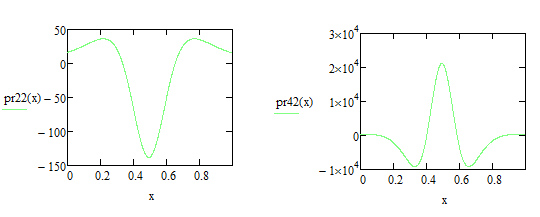
Для метода Трапеций получаем шаг h= 2.949852507375*10^-3

Количество разбиений Nraz=339

Для метода Симпсона получаем шаг h=0.038461538462 Количество разбиений Nraz=26

Результаты занесем в таблицу:

Метод	Полученное	Эталон (MathCad)	Погрешность
Трапеций	2.803697145995	2.803702168134	5.022138487298*10^-6
Симпсона	2.80370024723	2.803702168134	1.920903580643*10^-6

Вывод: В первой части работы мы сравнили между собой различные формулы численного интегрирования, для одинакового количества разбиений. Во второй части попытались достигнуть заданной точности, определяя шаг интегрирования по оценке остаточного члена. Как видно из результатов, с задачей удалось справиться.

Задание №7

Численное интегрирование. Квадратурные формулы типа Гаусса .

1. Вычислить интегралы, используя квадратурные формулы типа Гаусса (N - натуральное число):

а) , в качестве узлов квадратурной формулы взять корни многочлена Лежандра седьмой степени.

б) , в качестве узлов квадратурной формулы взять корни многочлена Чебышева седьмой степени.

в) , в качестве узлов квадратурной формулы взять корни многочлена Чебышева-Лагерра седьмой степени;

г) , в качестве узлов квадратурной формулы взять корни многочлена Чебышева-Эрмита седьмой степени.

Вычислить точные значения этих интегралов и сравнить их с полученными приближенными значениями.

Решение

Данные интегралы необходимо вычислить с помощью квадратурных формул Гаусса:

В отличие от формул Ньютона – Котеса здесь неизвестными являются не только веса квадратурной формулы W_i, но и узлы интегрирования.

Полагаем, что функция непрерывна на , и интеграл существует. Тогда, согласно теории, мы гарантируем существование на отрезке [α;β] полной системы ортогональных многочленов P_m(x) с весом ρ(x). Причём, все корни этих многочленов действительны и лежат, внутри вышеуказанного отрезка. Далее в теории показано, что узлами интегрирования для квадратурной формулы Гаусса на отрезке [α;β] будут корни ортогонального многочлена степени, равной количеству узлов, т.е. P_n(x). Тем самым, мы найдём узлы интегрирования. Далее находим веса W_i.

Рассмотрим первый интеграл:

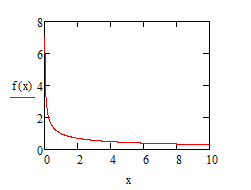
График подынтегральной функции выглядит следующим образом:

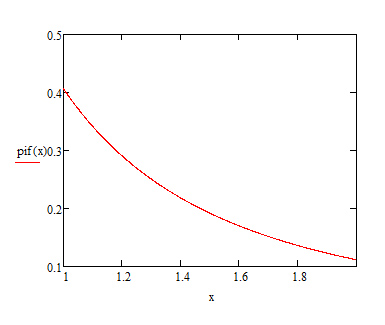
Данный интеграл не имеет особенностей на отрезке интегрирования. В качестве узлов квадратурной формулы используем корни многочлена Лежандра седьмой степени.

Многочлен Лежандра седьмой степени:

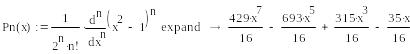
Найдем корни этого многочлена:

i	Xi
1	0
2	0.9491079123
3	-0.9491079123
4	0.4058451514
5	-0.4058451514
6	0.7415311856
7	-0.7415311856

Поскольку многочлен Лежандра определен на отрезке [-1,1], так же нужно преобразовать интеграл к этому отрезку:

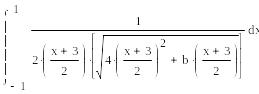
Далее находим веса по формулам:

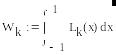
L_k(x) - многочлены степени n-1 из интерполяционной формулы Лагранжа.

Выпишем результаты вычислений:

Точное значение	Вычисленное значение	Погрешность
0.21270594937	0.212705949322	4.801231634488*10^-11

Рассмотрим второй интеграл:

График подынтегральной функции выглядит следующим образом:

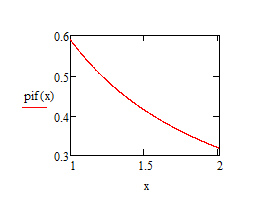
Данный интеграл не имеет особенностей на отрезке интегрирования. В качестве узлов квадратурной формулы используем корни многочлена Чебышева седьмой степени.

Многочлен Чебышева седьмой степени:

Найдем корни этого многочлена:

i	Xi
1	0
2	-0.781831482468
3	0.781831482468
4	-0.433883739118
5	0.433883739118
6	-0.974927912182
7	0.974927912182

Поскольку многочлен Чебышева определен на отрезке [-1,1], так же нужно преобразовать интеграл к этому отрезку:

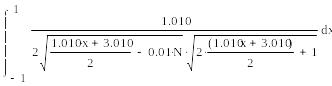
Далее находим веса по формулам:

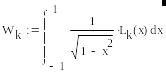
L_k(x) - многочлены степени n-1 из интерполяционной формулы Лагранжа.

Выпишем результаты вычислений:

Точное значение	Вычисленное значение	Погрешность
0.429977225437	0.686660090998	0.256682865562

Рассмотрим третий интеграл:

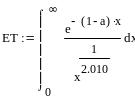
График подынтегральной функции выглядит следующим образом:

Данный интеграл имеет две особенности на отрезке интегрирования. В качестве узлов квадратурной формулы используем корни многочлена Чебышева-Лагерра седьмой степени. Многочлен Чебышева-Лагерра:

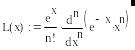
Найдем корни этого многочлена:

i	Xi
1	18.531775734301
2	11.992991079294
3	7.556617122754
4	4.391839708202
5	2.182134781362
6	0.773136044636
7	0.08550552945

Далее находим веса по формулам:

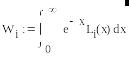
L_k(x) - многочлены степени n-1 из интерполяционной формулы Лагранжа.

Выпишем результаты вычислений:

Точное значение	Вычисленное значение	Погрешность
28.274525586839606821	28.024956081989632	0.24956950485

Рассмотрим четвертый интеграл:

График подынтегральной функции выглядит следующим образом:

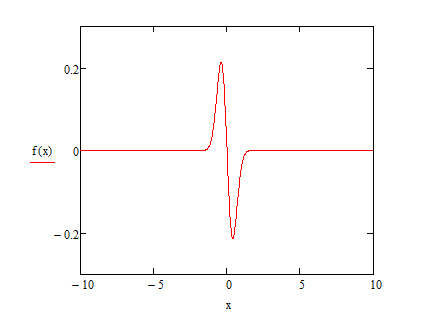
Данный интеграл имеет две особенности на границах отрезка интегрирования. Отметим, что подынтегральная функция четная, следовательно, интеграл должен равняться нулю. В качестве узлов квадратурной формулы используем корни многочлена Чебышева-Эрмита седьмой степени. Многочлен Чебышева-Эрмита:

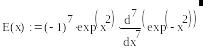
Найдем корни этого многочлена:

i	Xi
1	-1.673551628767471445
2	1.673551628767471445
3	-0.81628788285896466304
4	0.81628788285896466304
5	-2.6519613568352334924
6	2.6519613568352334924
7	0

Далее находим веса по формулам:

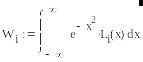
L_k(x) - многочлены степени n-1 из интерполяционной формулы Лагранжа.

Выпишем результаты вычислений:

Точное значение	Вычисленное значение	Погрешность
0	0	0

Вывод: Квадратурные формулы Гаусса – еще один, достаточно точный, метод численного интегрирования. В нашем случае, хорошую точность мы получили в первом и последнем интеграле. В последнем интеграле полученный численно интеграл полностью совпал с ожидаемым результатом, т.к. интеграл от четной функции на симметричном промежутке равняется нулю. В остальных примерах, точность достаточно мала. Это может быть связано как с особенностями функции, так и с особенностями расположения корней ортогональных многочленов.

Задание №8

Численное интегрирование. Приближенное вычислении несобственных интегралов.

Вычислить с точностью трех значащих цифр несобственные интегралы (N - натуральное число):

а) ;

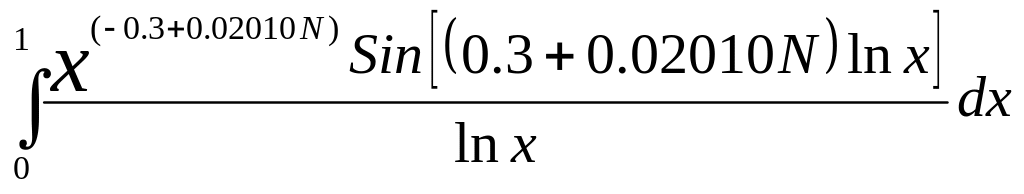б)

в)

Для всех вышеприведенных интегралов использовать формулу Симпсона и указать реальные пределы интегрирования с обоснованием их выбора для достижения указанной точности. В случае преобразования интегралов (например, избавление от особенностей) указать, как это проделано. Вычислить точные значения этих интегралов и сравнить их с полученными приближенными значениями.