Решение.

Перед началом приближения рассмотрим заданную функцию в указанных узлах. Для этого вычислим таблицу узлов:

№	x	f(x)
0	-2	7.042288255961544e17
1	-1.9	1.2430492962976978e16
2	-1.8	2.1928279165993256e14
3	-1.7	3.865837554365268e12
4	-1.6	6.810587474269461e10
5	-1.5	1.1989583273512971e9
6	-1.4	2.108996639315317e7
7	-1.3	3.70655430678546e5
8	-1.2	6.508096332930608e3
9	-1.1	114.15329780333643
10	-1.0	2

Необходимо найти многочлен четвёртой степени вида , который минимизирует следующее выражение , где x_i заданные узлы. Для нахождения коэффициентов многочлена воспользуемся системой линейных уравнений вида: _{, где N – число узлов, M – степень многочлена, ρi - весовые функции.}

Вычисленные коэффициенты заносим в таблицу:

Коэффициенты многочлена P4(x)
A0	-606.825809005
A1	-719.626644029
A2	-319.313623878
A3	-62.8351402068
A4	-4.62765383575

Далее вычисляем точки, получаем значения многочлена в этих точках и сравниваем с точными значениями:

№	xi	f(xi)	P4(xi)	| f(xi) - P4(xi)|
1	-1.9	1.2430492963e16	1.5294632554e17	1.4051583258e17
2	-1.8	2.1928279166e14	-4.4808837615e16	4.5028120406e16
3	-1.7	3.8658375544e12	-7.1631939402e16	7.1635805239e16
4	-1.6	6.8105874743e10	-2.4596906102e16	2.4596974208e16
5	-1.5	1.1989583274e9	2.8239613874e16	2.8239612675e16
6	-1.4	2.1089966393e7	4.7838249988e16	4.7838249967e16
7	-1.3	3.7065543068e5	2.4176909578e16	2.4176909578e16
8	-1.2	6.5080963329e3	-2.3749222147e16	2.3749222147e16
9	-1.1	114.1532978033	-4.7927682103e16	4.7927682103e16
10	-1	2	2.8671270668e16	2.8671270668e16
11	-0.9	0.0349967714	3.12094655e17	3.12094655e17
12	-0.8	6.1153823558e-4	9.3740676758e17	9.3740676758e17
13	-0.7	1.0669596772e-5	2.068689183e18	2.068689183e18
14	-0.6	1.8583166589e-7	3.8990407537e18	3.8990407537e18
15	-0.5	3.2302902093e-9	6.6505776101e18	6.6505776101e18
16	-0.4	5.6026837921e-11	1.057443316e19	1.057443316e19
17	-0.3	9.6925924754e-13	1.595075809e19	1.595075809e19
18	-0.2	1.6718414282e-14	2.3088720364e19	2.3088720364e19
19	-0.1	0	3.2326505224e19	3.2326505224e19
20	0	0	4.4031315189e19	4.4031315189e19

Из таблицы видно, что погрешность является довольно большой. Это, как и в лабораторной работе №1, связано с быстрой растущей функцией. Но в точках, по которым был построен многочлен P₄(x), погрешность является не столь большой, как в точках, по которым приближение не проводилось. Это означает, что метод дает нормальное приближение только в тех узлах, по которым строится многочлен, но это лишь общие слова, так как погрешность везде больше 100%.

Для лучшей наглядности приведём графики функции и многочлена P₄(x):

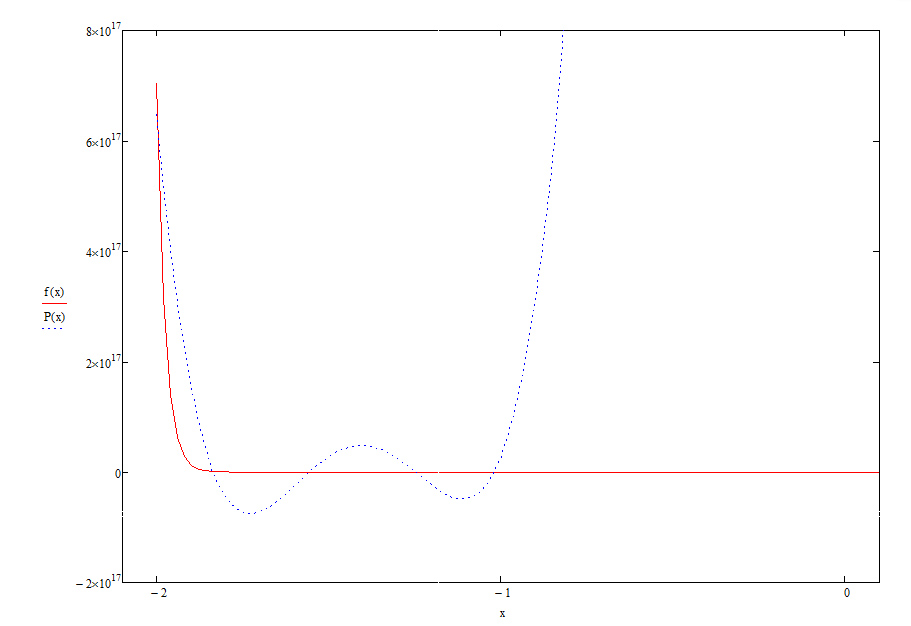
Во второй части нам необходимо приблизить непрерывно заданную функцию посредством ортогональных многочленов Лежандра и Чебышева четвёртой и восьмой степени.

Полиномы Лежандра:

=1

=x

=

=

=

=

=

=

=

Полиномы Чебышева:

=1

=x

=

=

=

=

=

Ортогональные многочлены Лежандра и Чебышева определены при условии, что , а нам необходимо приблизить функцию на отрезке . Поэтому сделаем замену переменной .

Затем представляем полученную после замены функцию в виде линейной комбинации ортогональных многочленов, неизвестные коэффициенты a_i найдём из условия ортогональности многочленов. Результаты заносим в таблицу:

Полиномы Лежандра:

X	f(X)	P4(x)	|P4(x)-f(x)|	P8(x)	|P8(x)-f(x)|
0.5	1.455	1.3323737026	0.1226262974	1.417401052	0.037598948
1.2	0.344	0.259917359	0.084082641	0.2538348021	0.0901651979
2.4	0.008	0.0367944006	0.0287944006	0.0139285632	0.0059285632

Полиномы Чебышева:

X	f(X)	T4(x)	|T4(x)-f(x)|	T8(x)	|T8(x)-f(x)|
0.5	1.455	1.3876012939	0.0673987061	1.4132256654	0.0417743346
1.2	0.344	0.2478817849	0.0961182151	0.2418068913	0.1021931087
2.4	0.008	0.0729647711	0.0649647711	-0.0156638591	0.0236638591

Для наглядности построим графики функции и полученных полиномов (в переменных x’):

Многочлены Лежандра:

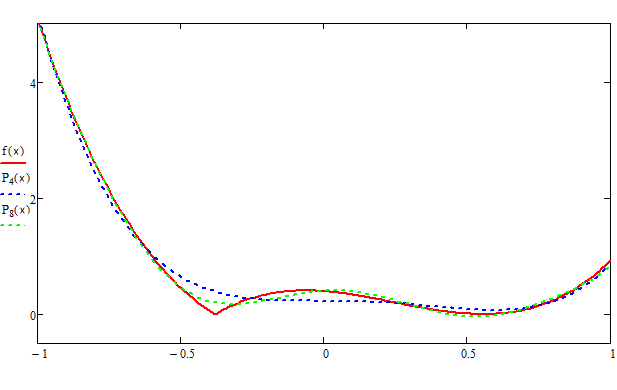
Многочлены Чебышева:

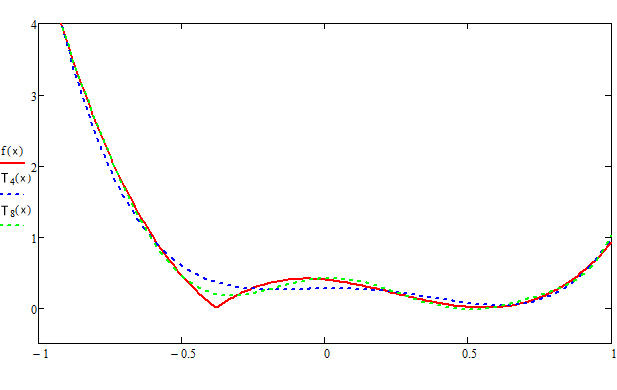
Вывод: В первой части из-за быстро растущей функции получить не удалось. Во второй методы дают точность до второго знака, значительно ухудшающуюся в точках излома функции.

Задание №4

Численное дифференцирование. Интерполяционные многочлены Ньютона, Лагранжа, формулы Стирлинга /3,9,19/.

Для функции , где N - натуральное число, составить таблицу значений функции для аргументов

По значениям функции в этой таблице найти значения первой и второй производных указанной функции в точках и с точностью ,

используя:

а) интерполяционный многочлен Лагранжа;

б) интерполяционный многочлен Ньютона;

в) формулу Стирлинга.

Решение.

Перед началом интерполирования рассмотрим заданную функцию в указанных узлах. Для этого вычислим таблицу узлов и установим расположение заданных точек, получим:

№	x	f(x)
1	0	7.3890560989
2	0.01	7.6282339195
3	0.02	8.0371088281
4	0.03	8.5703487151
5	0.04	9.224477323
6	0.05	10.0063246784
7	0.06	10.928655364
8	0.07	12.0090567415
9	0.08	13.2698354444
10	0.09	14.7383848497
11	0.1	16.4478605798
12	0.11	18.43811909
13	0.12	20.7569232678
14	0.13	23.4614456913
15	0.14	26.620119708
16	0.15	30.3149065957
17	0.16	34.6440665652
18	0.17	39.7255440224
19	0.18	45.7011048294
20	0.19	52.7413968109

Построим график исходной функции:

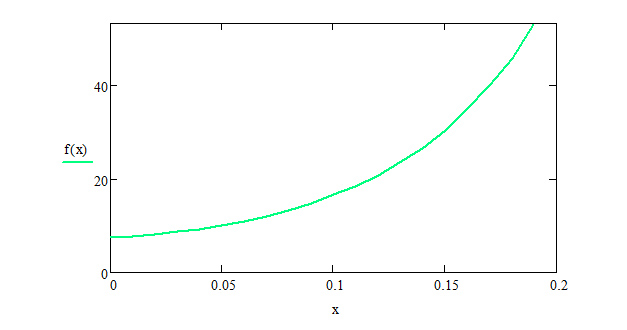
Вычислим точные значения первой и второй производных в нужных точках:

x	f’(x)	f”(x)
0.6	99.8047759218	1576.8216114093
0.14	341.181372147	5347.6140346165

Построим графики первой и второй производной:

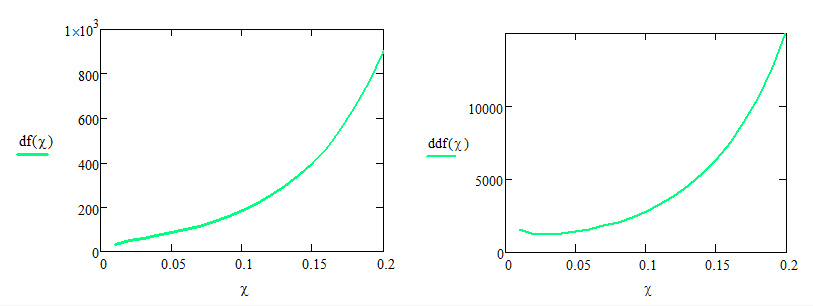
Сначала необходимо выяснить необходимое количество узлов для того чтобы вычислить значения производных в заданных точках с заданной точностью. Из теории нам известно лишь то, что порядок точности по отношению к шагу h равен количеству узлов интерполяции минус порядок производной. В этом выражении не присутствуют ни условия для конкретных функций, ни целесообразность выбора того или иного шага.

Поэтому пробуем вычислить производные, используя аппроксимацию по 7-ми точкам. В случае недостаточной точности будем постепенно изменять шаг и добиваться наилучшего результата.

1. Интерполяционный многочлен Лагранжа.

Заданную на отрезке функцию , имеющую непрерывные производные до -го порядка, представляем в виде равенства , где – интерполяционный полином степени , построенный по узлам интерполяции , – остаточный член. Полагаем:

абсолютные погрешности этих приближённых равенств определяются абсолютными значениями соответственно .

Взяв в равенстве в качестве интерполяционный полином Лагранжа и продифференцировав его, получим необходимые производные:

Полученные результаты для многочлена 6-ой степени заносим в таблицу:

x=0.06	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	99.8047759218	99.8045931358	0.0001827859
	1576.8216114093	1576.826522729	0.0049113196

x=0.14	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	341.181372147	341.1814599198	0.0000877728
	5347.6140346165	5347.6145177085	0.000483092

Как видно из таблицы получить нужный результат удалось далеко не везде. Как и планировали, будем уменьшать шаг. Посмотрим, в какой момент мы достигнем точности 10^-5 , и в какой получим максимально возможную точность. Будем последовательно уменьшать шаг в 10 раз.

Результаты выведем только для точки x=0.06.

H=0.001

x=0.06	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	99.8047759218	99.8047759216	1.4490808553*10^-10
	1576.8216114093	1576.8216114405	3.1157014746*10^-8

H=0.0001

x=0.06	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	99.8047759218	99.8047759215	2.9938007629*10^-10
	1576.8216114093	-	-

С шагом H=0.0001 значение для второй производной получить не удалось, а погрешность для первой производной выросла.

Незатруднительно оказалось увидеть и то, что при банальном увеличении шага в 2 раза, получается результат необходимой точности:

H=0.005

x=0.06	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	99.8047759218	99.8047735525	2.3692371514*10^-6
	1576.8216114093	1576.8216755316	6.4122289132*10^-5

Для остальных методов будем вычислять производные только с заданным шагом (так как в возможности достижения нужной точности мы убедились, а открытым остался вопрос о сравнении различных методов).

2) Многочлен Ньютона.

Для нахождения производных функцию приближённо заменим интерполяционным полиномом Ньютона, построенным для системы узлов , получим:

Введем обозначение

Далее полагаем:

Полученные результаты для многочлена 6-ой степени заносим в таблицу:

x=0.06	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	99.8047759218	99.806145744	0.00136982
	1576.8216114093	1576.5910333544	0.2305780549

x=0.14	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	341.181372147	341.1398948875	0.04147726
	5347.6140346165	5347.3073876511	0.3066469654

3. Многочлен Стирлинга.

Пусть - система равноотстоящих точек с шагом и - соответствующие значения функции . Полагая и заменяя приближённо функцию интерполяционным полиномом Стирлинга, будем иметь:

,

где для краткости введены обозначения:

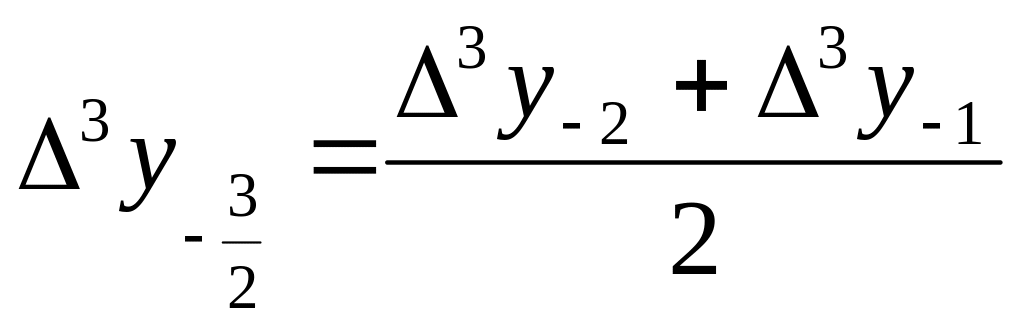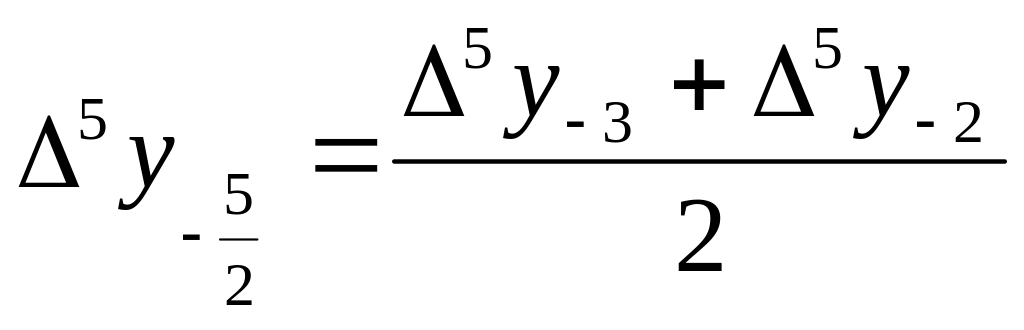; ; , где ;

Взяв в качестве нужной точки , , получим:

;

Многочлен построим для 8-ми точек (попробуем проверить отсутствие повышенной точности). Полученные результаты занесем в таблицу:

x=0.06	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	99.8047759218	99.8045931358	1.8278593419*10^-4
	1576.8216114093	1576.8265227286	4.9113218333*10^-3

x=0.14	Точное значение (MathCAD)	Вычисленное значение	Погрешность
	341.181372147	341.1814599198	8.7772795837*10^-5
	5347.6140346165	5347.6140346133	4.8309532212*10^-4

Вывод: В ходе работы были изучены различные методы численного дифференцирования. Погрешности методов в работе напрямую зависели от конкретного вида функции, из-за этого было затруднительно теоретически оценить погрешность и, для достижения заданной точности, нам пришлось работать с изменением начального шага. Методы Лагранжа и Стирлинга на начальном шаге дали немного более точный результат.

Задание №5

Численное дифференцирование. Метод неопределенных коэффициентов. Уточнение по методу Рунге-Ромберга /13,19/.

1. Получить методом неопределенных коэффициентов формулу для вычисления первой производной функции . Значения вычислить в точках , где N - натуральное число , .

Вычислить по полученной формуле значение первой производной в точке и .

Сравнить полученное значение первой производной с "точным" значением в этих же точках.

2. Найти значения первой производной функции , где - натуральное число, в точке по формуле , где , , , а остаточный член . Уточнить полученные значения первой производной по методу Рунге-Ромберга для (т.е. новый шаг ). Сравнить полученные значения первой производной, как уточненные, так и не уточненные, с "точными" значениями. В случае, когда уточнить не удается, подобрать шаг таким образом, чтобы результат был ближе к точному значению. Выбор шага обосновать.

Решение.

1. Вычислим таблицу узлов и установим расположение заданных точек, получим:

№
0	2010	5.6108035511e133
1	2010.14	5.6712886214e133
2	2010.28	5.7324235874e133
3	2010.42	5.7942154092e133
4	2010.56	5.8566711211e133

Для получения формул дифференцирования с помощью неопределенных коэффициентов применим метод рядов Тейлора. Получим формулу для вычисления первой производной функции в виде , где – неопределенные коэффициенты.

Так как используются равноотстоящие узлы, для точки получим:

.

Раскладывая в ряд Тейлора в окрестности точки , получим:

.

Мы хотим обеспечить условия, при которых сумма в правой части приближает с возможно меньшей погрешностью. Получаем для систему уравнений:

Решив которую, получим:

Формула приближенного вычисления производной в точке будет иметь вид:

.

Для точки получим:

.

Раскладывая функции в ряд Тейлора в окрестности точки , получим:

.

Мы хотим обеспечить условия, при которых сумма в правой части приближает с возможно меньшей погрешностью. Получаем для систему уравнений:

Решив которую, получим: .

Формула приближенного вычисления производной в точке будет иметь вид:

.

Полученные результаты занесем в таблицу:

	Точное (MathCAD)	Вычисленное	Погрешность
	4.3434903062*10^132	4.343490309*10^132	2.8323082485*10^123
	4.4373277308*10^132	4.4373277336*10^132	2.7845416692*10^123

2. Рассмотрим заданную функцию:

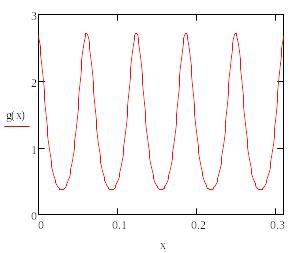
Из графика видно, что функция является периодической, подсчитаем период, найдя соседние максимум и минимум:

Найдем значения первой производной по заданной формуле:

где ,

Шаг	Точное (MathCAD)	Вычисленное	Погрешность
3.926990817*10^-3	-80.4424930566	-81.4590462692	1.0165532126

Попробуем уточнить полученное значение по методу Рунге-Ромберга для r=3. Найдем значения производной с новым шагом:

Шаг	Точное (MathCAD)	Вычисленное	Погрешность
0.0117809725	-80.4424930566	-81.4226275241	0.9801344675

Затем уточняем:

Точное (MathCAD)	Уточненное	Погрешность
-80.4424930566	-81.46359861229112	1.021105555721775

Как видно из таблицы, при уточнении по методу Рунге-Ромберга результат только ухудшился. Этот результат получился в силу того, что мы использовали шаг приблизительно равный половине периода. Уменьшим заданный шаг в 10 раз и проведем заново те же самые операции:

Шаг	Точное (MathCAD)	Вычисленное	Погрешность
3.926990817*10^-4	-80.442493056569	-80.4539341988	0.0114411422

Попробуем уточнить полученное значение по методу Рунге-Ромберга для r=3. Найдем значения производной с новым шагом:

Шаг	Точное (MathCAD)	Вычисленное	Погрешность
0.001178097245	-80.4424930566	-80.5445270037	0.1020339471

Затем уточняем:

Точное (MathCAD)	Уточненное	Погрешность
-80.442493056569	-80.442610098168	1.17041598287*10^-4

На этом этапе видно, что метод Рунге-Ромберга уменьшил погрешность на 2 порядка, относительно изначальной. Для получения более точного результата будем работать с изменением шага. Последовательно будем уменьшать шаг в некоторое количество раз, пока не добьемся минимума погрешности. Проделав данную процедуру можно убедиться, что наибольшая точность достигается при шаге в 450000 раз меньше начального:

Шаг	Точное (MathCAD)	Вычисленное	Погрешность
3.490658504*10^-8	-80.4424930566	-80.4424930558	7.8715345353*10^-10

Попробуем уточнить значение, которое мы получили изменением шага, по методу Рунге-Ромберга для r=3. Найдем значения производной с новым шагом:

Шаг	Точное (MathCAD)	Вычисленное	Погрешность
1.04719755119*10^-7	-80.4424930566	-80.4424930584	1.8632988485*10^-9

Затем уточняем:

Точное (MathCAD)	Уточненное	Погрешность
-80.442493056569	-80.442493055451	1.11846532036*10^-9

Вывод: Метод неопределенных коэффициентов дал относительно неплохую точность для значений функции порядка 10¹³², но оказался достаточно сложным для практических вычислений. Метод Рунге-Ромберга позволил добиться нужного результата при выполнении некоторых теоретических оценок.

Задание №6

Численное интегрирование. Формулы трапеции, Симпсона, Ньютона – Котеса /2,8,9,17,19/ .

1.Вычислить интегралы:

а) , где и - натуральное число

б) 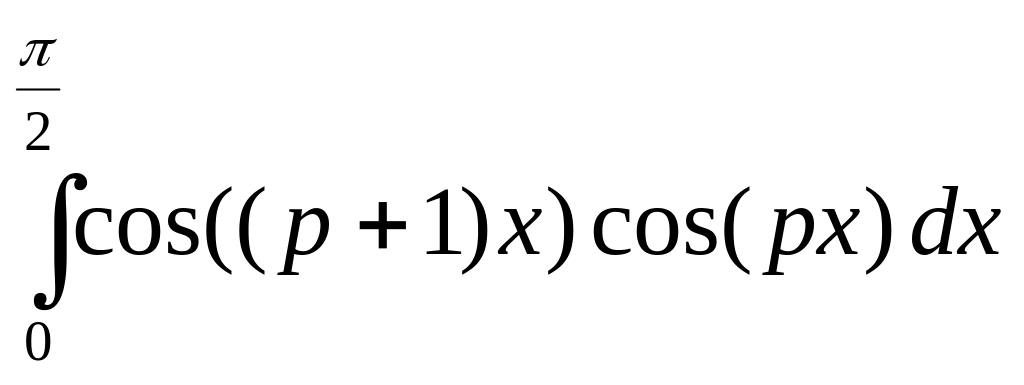, где и - натуральное число - по формулам трапеций, Симпсона, Ньютона-Котеса. Число разбиений отрезка интегрирования во всех случаях положить равным 20. Сравнить полученные приближенные значения между собой и с точными значениями соответствующих интегралов.

2. Вычислить интегралы:

а) , где и - натуральное число;

б) , где - натуральное число;

по формуле трапеций и Симпсона с точностью , определяя шаг интегрирования по оценке остаточного члена. Указать конкретные значения полученных шагов интегрирования.