Решение.
N=4. Нам дана периодическая
функция, необходимо приблизить ее с
помощью тригонометрических многочленов.
Для решения этой задачи воспользуемся
разложением функции
в
тригонометрический ряд Фурье.
Прежде чем начинать построение полиномов,
доопределим функцию на концах отрезка
значением
.
В общем случае тригонометрический ряд Фурье имеет вид:
Тригонометрические полиномы степеней (3+N) и (15+N) получим из ряда Фурье, взяв соответственно первые (3+N) и (15+N) членов этого ряда.
Тригонометрический ряд Фурье для нашей функции имеет вид:
Полином степени (3+N) имеет вид:
Полином степени (15+N) имеет вид:
Далее по полученным формулам вычисляем значения полиномов P1(x), P2(x) в требуемых точках . Затем сравниваем полученные значения тригонометрических полиномов в одинаковых точках и оцениваем разность значений. Результаты заносим в соответствующие таблицы.
Таблица коэффициентов
и
:
№ |
P1(x) |
P2(x) |
||
|
|
|
|
|
1 |
0.198549523842 |
-0.368957660285 |
0.198549523842 |
-0.368957660285 |
2 |
0.00314414225 |
-0.159655409394 |
0.00314414225 |
-0.159655409394 |
3 |
0.019455369841 |
-0.12230024906 |
0.019455369841 |
-0.12230024906 |
4 |
0.002946304293 |
-0.080644728307 |
0.002946304293 |
-0.080644728307 |
5 |
0.005301085414 |
-0.072610443081 |
0.005301085414 |
-0.072610443081 |
6 |
0.002637737169 |
-0.054485786282 |
0.002637737169 |
-0.054485786282 |
7 |
0.001679554245 |
-0.05114287198 |
0.001679554245 |
-0.05114287198 |
8 |
- |
- |
0.002257679371 |
-0.041551003007 |
9 |
- |
- |
0.000452845974 |
-0.039150869721 |
10 |
- |
- |
0.001833792764 |
-0.03378129768 |
11 |
- |
- |
0.000057800192 |
-0.031561319054 |
12 |
- |
- |
0.001402756591 |
-0.028559665021 |
13 |
- |
- |
0.000003665304 |
-0.026368312626 |
14 |
- |
- |
0.000948343448 |
-0.024746047053 |
15 |
- |
- |
0.000085146295 |
-0.022652974833 |
16 |
- |
- |
0.000648736981 |
-0.021791717047 |
17 |
- |
- |
0.000200458718 |
-0.01990383236 |
18 |
- |
- |
0.000371380662 |
-0.019406834149 |
19 |
- |
- |
0.000299033995 |
-0.017812218266 |
Таблица результатов:
№ |
x |
f(x) |
P1(x) |
P2(x) |
1 |
-1.9 |
0 |
-0.055784252017527 |
0.050820769570876 |
2 |
-1.8 |
0 |
-0.014908439956668 |
0.025244688573866 |
3 |
-1.7 |
0 |
0.038283871772241 |
0.016060799710706 |
4 |
-1.6 |
0 |
-0.037699679480439 |
0.011347188151752 |
5 |
-1.5 |
0 |
0.020638907155715 |
0.008398060670398 |
6 |
-1.4 |
0 |
0.001113746663968 |
0.006114386279772 |
7 |
-1.3 |
0 |
-0.016486293934666 |
0.004419146311665 |
8 |
-1.2 |
0 |
0.021930269885547 |
0.002917794334715 |
9 |
-1.1 |
0 |
-0.009624910359844 |
0.001089321297658 |
10 |
-1.0 |
0.08 |
0.075342114977187 |
0.081705854317436 |
11 |
-0.9 |
0.18 |
0.199541512144186 |
0.179823890448605 |
12 |
-0.8 |
0.28 |
0.256581071458397 |
0.278155159984052 |
13 |
-0.7 |
0.38 |
0.397645410860853 |
0.376212994842096 |
14 |
-0.6 |
0.48 |
0.481333481450298 |
0.474123438171918 |
15 |
-0.5 |
0.58 |
0.55688887180542 |
0.571441030428537 |
16 |
-0.4 |
0.68 |
0.718377906577822 |
0.667802480971782 |
17 |
-0.3 |
0.78 |
0.742069951988755 |
0.762519871590574 |
18 |
-0.2 |
0.88 |
0.888610992830736 |
0.853046760967989 |
19 |
-0.1 |
0.98 |
1.042821576650911 |
0.926870833556152 |
20 |
0 |
1.08 |
0.525313181659199 |
0.533874821951544 |
Таблица погрешностей:
№ |
|P1(x) -f(x)| |
|P2(x) -f(x)| |
|P1(x) –P2(x)| |
1 |
0.055784252017527 |
0.050820769570876 |
0.106605021588403 |
2 |
0.014908439956668 |
0.025244688573866 |
0.040153128530534 |
3 |
0.038283871772241 |
0.016060799710706 |
0.022223072061535 |
4 |
0.037699679480439 |
0.011347188151752 |
0.049046867632191 |
5 |
0.020638907155715 |
0.008398060670398 |
0.012240846485317 |
6 |
0.001113746663968 |
0.006114386279772 |
0.005000639615803 |
7 |
0.016486293934666 |
0.004419146311665 |
0.020905440246331 |
8 |
0.021930269885547 |
0.002917794334715 |
0.019012475550832 |
9 |
0.009624910359844 |
0.001089321297658 |
0.010714231657502 |
10 |
0.004657885022814 |
0.001705854317436 |
0.00636373934025 |
11 |
0.019541512144186 |
0.000176109551395 |
0.019717621695581 |
12 |
0.023418928541603 |
0.001844840015948 |
0.021574088525656 |
13 |
0.017645410860853 |
0.003787005157904 |
0.021432416018757 |
14 |
0.001333481450297 |
0.005876561828082 |
0.00721004327838 |
15 |
0.02311112819458 |
0.008558969571463 |
0.014552158623117 |
16 |
0.038377906577822 |
0.012197519028218 |
0.05057542560604 |
17 |
0.037930048011246 |
0.017480128409426 |
0.02044991960182 |
18 |
0.008610992830736 |
0.026953239032011 |
0.035564231862747 |
19 |
0.062821576650911 |
0.053129166443848 |
0.11595074309476 |
20 |
0.554686818340801 |
0.546125178048456 |
0.008561640292345 |
Для лучшей наглядности приведём графики функции и многочленов P1(x), P2(x). На рисунке №1: f(x) – график функции; P1(x) – график тригонометрического многочлена степени (3+N); P2(x) – график тригонометрического многочлена степени (15+N).
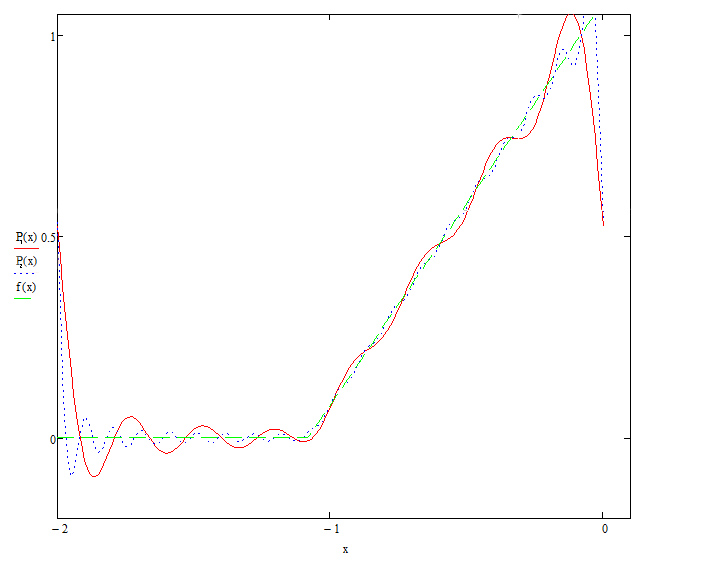
Вывод: исследованный метод достаточно удобен с точки зрения его программирования в MathCAD’e, и при этом дает приличную точность, даже в точках излома функции. Точность интерполирования увеличивается при увеличении порядка тригонометрического многочлена. Наибольшая точность достигается в середине отрезка.
Задание №3
Среднеквадратическое приближение функций (случай дискретных точек, полиномы Лежандра и Чебышева) /10,19/.
1. Задана
функция
,
где N
- натуральное число. Вычислить значение
этой функции в точках
.
Среди многочленов 4 степени
найти такой, который минимизирует
выражение
.
Вычислить значение полученного многочлена
в точках
и сравнить их с "точными" значениями
функции
в этих точках.
2. Для
функции
,
,
где
N
- натуральное число, на отрезке
найти приближения функций при помощи
полиномов Лежандра
;
,
полиномов Чебышева
.
Для каждого приближения вычислить
значения в точках
и сравнить с "точным" значением
функции
и между собой в этих же точках.