Решение.

N=4. Перед началом интерполирования рассмотрим заданную функцию в указанных узлах. Для этого вычислим таблицу узлов и установим расположение заданных точек, получим:

№	x	f(x)
0	-0.2150537634	5.1866424253e-6
1	-0.1612903226	1.086837791e-4
2	-0.1075268817	2.2774201249e-3
3	-0.0537634409	0.0477223231
4	0	1
5	0.0537634409	20.9545540623
6	0.1075268817	439.0933359505
7	0.1612903226	9.2010050466e3
8	0.2150537634	1.9280295768e5
9	0.2688172043	4.0401e6
10	0.3225806452	8.4658493867e7
11	0.376344086	1.7739809866e9
12	0.4301075269	3.7172980489e10
13	0.4838709677	7.7894322931e11

x₁= -0.1315789474

x₂= 0.3947368421

f(x₁)= 4.9751243781*10^-4

f(x₂)= 8.120601*10⁹

Для построения интерполяционных многочленов 5-ой степени нам потребуется взять 6 узлов из 14-ти. Для этого обратимся к теории.

Остаточный член интерполяционной формулы в форме Лагранжа или Ньютона имеет вид: .

Про известно только, что . Оценки, полученные таким образом, имеют, как правило, качественный характер, поскольку отсутствие информации о значении не дает возможности провести точные количественные вычисления. Но они дают возможность сделать некоторые рекомендации по выбору узлов интерполяции x₁, x₂,…,x_n+1. Можно выбрать узлы так, чтобы минимизировать произведение перед производной вблизи требуемой точки . Минимизация этого выражения показывает, что эти узлы должны располагаться с обеих сторон от точки и по возможности так, чтобы был центром интервала .

Для нашей функции остаточный член выглядит следующим образом:

Теперь последовательно для каждой возможной комбинации из 6-ти рядом стоящих узлов сделаем оценку погрешностей в точках и при и :

Погрешность
[0…5]	2.8115420333e-5	113.5891096883	2.7153029495	1.0970095446e7
[1…6]	1.7674382861e-3	7.1406274196e3	27.2120689985	1.0993947996e8
[2…7]	0.4073946923	1.6459152963e6	244.3786161326	9.8731404704e8
[3…8]	110.978063356	4.4836247376e8	1.8866270771e3	7.622162054e9
[4…9]	1.1627479142e4	4.697617848e10	1.1627479142e4	4.697617848e10
[5…10]	8.2840537696e5	3.3468405634e12	4.8729728056e4	1.9687297432e11
[6…11]	4.7116919983e7	1.9035706842e14	7.8546901615e4	3.1733733722e11
[7…12]	2.3037327764e9	9.30731079e15	1.496286633e5	6.0451476261e11
[8…13]	1.0093590356e11	4.0779114399e17	1.0451339715e6	4.2224457582e12

Так как x₁= -0.1315789474, эта точка располагается между 1-м и 2-м узлами. Точка x₂=0.3947368421 соответственно между 11-м и 12-м узлами. Следовательно, теоретически мы должны взять первые 6 узлов для приближения в точке и последние шесть узлов для приближения в точке .

Из таблицы видно, что нужного результата получить не удалось. Скорее всего такие данные получились из-за заданной функции , так как значение данной функции на правом конце достигает порядка 10¹¹, а значение производной порядка 10²².

Несмотря на полученные противоречия, построим интерполяционные многочлены Лагранжа и Ньютона для точки в узлах [0..6], а для точки в узлах [8..13], получим:

Для точки :

	Метод Лагранжа	Метод Ньютона
a0	1.0	1.0
a1	96.3673616898637	96.3673616898637
a2	2802.07257979207	2802.07257979207
a3	33047.0314166402	33047.0314166402
a4	167770.25387182	167770.25387182
a5	304424.72120224	304424.72120224
f(x1)	0.00049751243781095	0.00049751243781095
L(x1)	-0.17466637144332095	-0.17466637144332095
|f(x1)-L(x1)|	0.17516388388113188	0.17516388388113188

Для точки :

	Метод Лагранжа	Метод Ньютона
a0	-3.31194970799987e13	-3.31194970799987e13
a1	5.47227633054494e14	5.47227633054494e14
a2	-3.56274858247811e15	-3.56274858247811e15
a3	1.14334010849591e16	1.14334010849591e16
a4	-1.8099768274679e16	-1.8099768274679e16
a5	1.13163742215234e16	1.13163742215234e16
f(x2)	8.120601e9	8.120601e9
L(x2)	-4.6200995216e9	-4.6200995216e9
|f(x2)-L(x2)|	-1.2740700522e10	-1.2740700522e10

Как видно из таблицы многочлены Лагранжа и Ньютона равны при одинаковом количестве точек разбиения.

Для лучшей наглядности приведём графики функции и многочленов L(x), N(x):

Для точки :

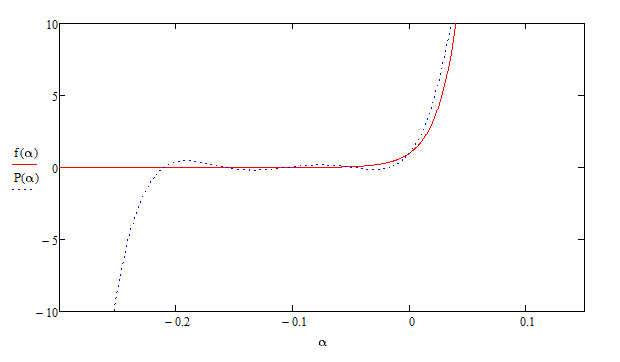
Для точки :

В нашем случае методы не дали хорошую точность из-за сильного возрастания заданной функции на нужном отрезке. Возможно, что в данном случае, для получения более точного результата нужно использовать меньшее количество узлов. В качестве дополнительного исследования попробуем использовать для интерполяции только 2 точки, т.е. просто приблизить функцию прямой. Используем 1-й и 2-й узел для точки , и 11-й и 12-й узел для точки .

Для точки

	Метод Лагранжа	Метод Ньютона
a0	0.0004191751891	0.0004191751891
a1	0.001966445597	0.001966445597
f(x2)	0.00049751243781095	0.00049751243781095
L(x2)	0.00016043234744057	0.00016043234744057
|f(x2)-L(x2)|	0.00033708009	0.00033708009

Для точки :

	Метод Лагранжа	Метод Ньютона
a0	2.460190155e11	2.460190155e11
a1	6.725809905e11	6.725809905e11
f(x2)	8.120601e9	8.120601e9
L(x2)	1.9473480738e10	1.9473480738e10
|f(x2)-L(x2)|	1.1352879738e10	1.1352879738e10

Из полученных таблиц видно, что прямая линия приближает данную функцию немного лучше, чем многочлен 5-ой степени.

Вывод: В ходе исследования видно, что методы Лагранжа и Ньютона дают одинаковые многочлены. В нашем случае методы не дали хорошую точность из-за сильного возрастания заданной функции на нужном отрезке, хотя полученный результат лежит в пределах теоретических расчетов. При использовании интерполирования по 2-м точкам получен относительно лучший результат, чем по 6-ти точкам. Для достижения наилучшего приближения функции такого вида необходимо последовательно уменьшать шаг задания узлов до достижения оптимальной точности.

Задание №2

Среднеквадратичные приближения с помощью тригонометрических полиномов /10,16,19/.

1. Считая функцию периодической с периодом 2 , получить ее приближение при помощи тригонометрических полиномов степеней (3+N) и (15+N), если:

где N - натуральное число.

С помощью полученных тригонометрических полиномов найти значение функции в точках и сравнить полученные значения тригонометрических полиномов для одинаковых значений координаты .