Продольно-поперечная разностная схема /6,7,10,13,18,20/.
Для дифференциальной задачи :
(1)
численно решить методом установления задачу на равномерной сетке , используя для решения продольно-поперечную схему (такая схема приведена в лекциях А. И. Голубева /6/).
Положим
,
N-натуральное число.
Численно вычислить порядок сходимости.
Решение:
Найдем точное решение исходной дифференциальной задачи. В данном случае точное решение можно не искать с помощью метода Фурье, а попробовать подобрать частное решение удовлетворяющее граничным условиям.
Будем искать решение в виде:
Тогда для неизвестных констант, используя граничные условия, получим следующие выражения:
,
Отсюда получаем решение:
График решения выглядит следующим образом:
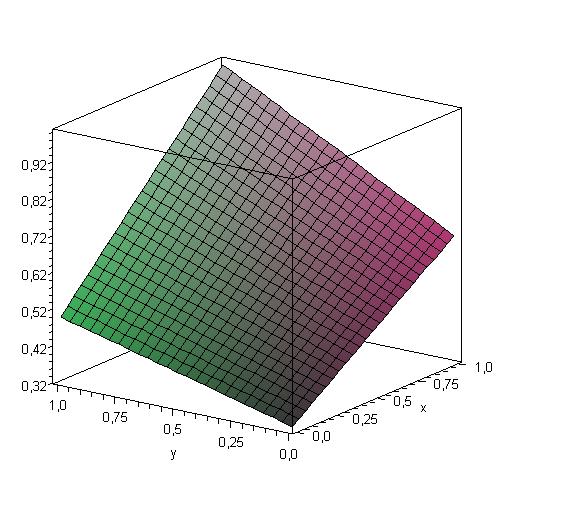
Перейдем к решению данной задачи.
Решение u(x,y) нашей задачи можно понимать как не зависящую от времени температуру в точке (x,y) пластинки, находящейся в тепловом равновесии. Функции в правой части уравнения и на границе означают в таком случае соответственно распределение источников тепла и температуру на границе. Из вида нашей задачи заключаем, что источников тепла нет.
Рассмотрим вспомогательную нестационарную задачу:
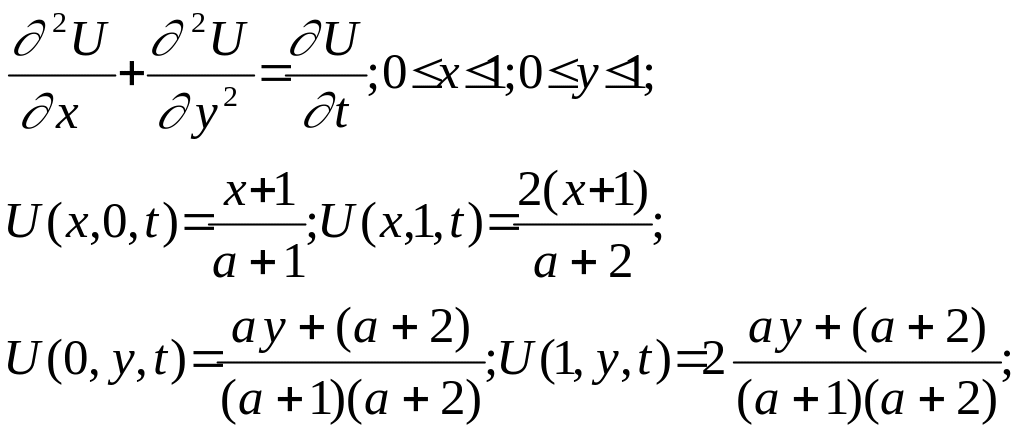(2)
Поскольку температура на границе не
зависит от времени, то естественно
ожидать, что решение
с течением времени будет меняться всё
медленнее, распределение температур
в пределе при
превращается в равновесное распределение
температур
,
описываемое задачей (1). Поэтому вместо
стационарной задачи (1) можно решить
нестационарную задачу (2) до того времени
t, пока её решение перестанет
меняться в пределах интересующей нас
точности. В этом и состоит идея решения
стационарных задач методом установления.
Введем в рассмотрение операторы
и запишем продольно поперечную схему в виде
(3)
Исключая
промежуточные значения
,
получим (индексы
опустим)
Преобразуем ее к канонической форме
где
Поставим
задачу выбрать в схеме (3) шаг
таким образом, чтобы разностное решение
задачи (2) выходило на стационарный режим
за наименьшее число шагов. Затухание
влияния начальных условий для схемы
(3) можно исследовать методом разделения
переменных. Для этого нам понадобятся
точные собственные функции операторов
и
и спектры их собственных значений.
Нетрудно убедиться, что оператор
имеет собственные функции
,
соответствующие собственным числам
В самом деле, находим, опуская индекс 1
у
,
Аналогично,
оператор –
имеет собственные функции
и собственные числа
При этом
.
Тогда собственные функции оператора
–
имеют вид
и собственные числа
.
Найдем множители роста для этих гармоник.
Полагая
из схемы (3) получим
.
Определим,
какие гармоники затухают наиболее
медленно. Множитель
монотонно убывает с ростом
.
Поскольку
то
либо 
где
Аналогично,
второй множитель максимален по модулю
либо при
,
либо при
.
Следовательно, максимальными множителями
роста будут
Из
этих выражений следует, что при малых
быстрее затухает гармоника
,
при больших 
.
Выберем шаг
таким образом, чтобы скорости затухания
этих гармоник стали одинаковы; этот шаг
и будет оптимальным:
Таким
образом, оптимальный шаг равен
(4)
Если
то
.
Для нашего случая a=1,
b=1 =>
.
Будем решать задачу (4), представленную в виде схемы (5) методом прогонки.
Вычисление
по уже известным
по схеме (3) осуществляется прогонками
в направлении оси Ох для вычисления
решений
одномерных задач при каждом фиксированном
i, а затем прогонками в
направлении оси Оу для вычисления
решений
одномерных задач при каждом фиксированном
j.
Предположим
что: 
(5)
и i
меняем на i-1, получим
.
Подставим последнее выражение в
уравнение (2), получим:
Сравнивая это выражение с (5), получаем:
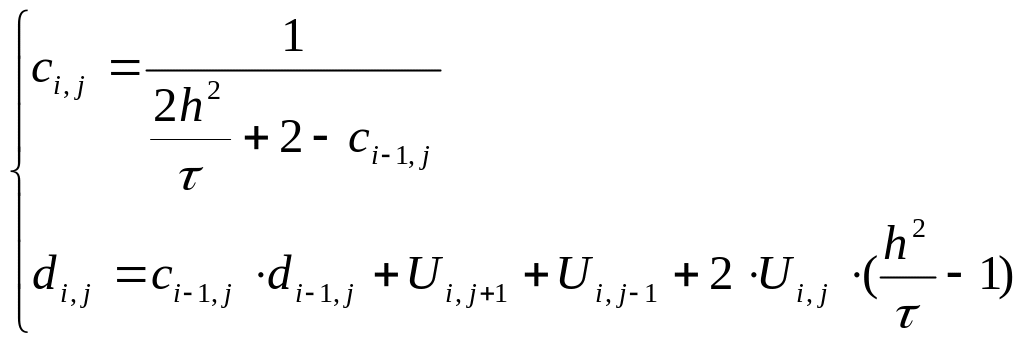
Подставим в (2) и (5) индекс m = 1, получим:
Далее ищем решение по формуле (5). Аналогично поступая со вторым уравнением (2), получаем:
Положим
и
.
Теперь, когда найдено аналитическое решение и все готово для счета, выполним необходимые вычисления. Результаты занесем в таблицы:
Полученное решение:
|
0.0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
0.0 |
0.331543 |
0.397852 |
0.464160 |
0.530469 |
0.596777 |
0.663086 |
0.2 |
0.364831 |
0.437797 |
0.510763 |
0.583730 |
0.656696 |
0.729662 |
0.4 |
0.398119 |
0.477743 |
0.557367 |
0.636991 |
0.716614 |
0.796238 |
0.6 |
0.431407 |
0.517689 |
0.603970 |
0.690251 |
0.776533 |
0.862814 |
0.8 |
0.464695 |
0.557634 |
0.650573 |
0.743512 |
0.836451 |
0.929390 |
1.0 |
0.497983 |
0.597580 |
0.697176 |
0.796773 |
0.896370 |
0.995966 |
Эталонное решение:
|
0.0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
0.0 |
0.331543 |
0.397852 |
0.464160 |
0.530469 |
0.596777 |
0.663086 |
0.2 |
0.364831 |
0.437797 |
0.510763 |
0.583730 |
0.656696 |
0.729662 |
0.4 |
0.398119 |
0.477743 |
0.557367 |
0.636991 |
0.716614 |
0.796238 |
0.6 |
0.431407 |
0.517689 |
0.603970 |
0.690251 |
0.776533 |
0.862814 |
0.8 |
0.464695 |
0.557634 |
0.650573 |
0.743512 |
0.836451 |
0.929390 |
1.0 |
0.497983 |
0.597580 |
0.697176 |
0.796773 |
0.896370 |
0.995966 |
Погрешность:
|
0.0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
0.0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.2 |
0 |
2.1e-9 |
3.5e-9 |
3.5e-9 |
2.1e-9 |
0 |
0.4 |
0 |
3.5e-9 |
5.7e-9 |
5.7e-9 |
3.4e-9 |
0 |
0.6 |
0 |
3.5e-9 |
5.7e-9 |
5.7e-9 |
3.4e-9 |
0 |
0.8 |
0 |
2.1e-9 |
3.5e-9 |
3.5e-9 |
2.1e-9 |
0 |
1.0 |
0 |
0 |
0 |
0 |
0 |
0 |
При увеличении в 10 раз
шагов по x и y,
а так же количества итераций порядок
сходимости оказался равным: p
5
Вывод: Одна из самых сложных лабораторных работ. Достаточно сложная теория, громоздкий метод прогонки. Однако результаты получились очень хорошими.