Разностная схема - ’’ крест ’’ /6,7,10,13,18,20/.
Для дифференциальной задачи :
a=2
методом
конечных разностей численно найти
решение при
,.
Для численного
решения использовать шаблон разностной
схемы - ’крест’ с аппроксимацией
начальных данных
,
где
- шаг по времени (такая схема приводится
в лекциях А. И. Голубева /6/)
Численно вычислить порядок сходимости.
Решение.
Построим для нашего дифференциального уравнения гиперболического типа разностную схему «крест».
Введем прямоугольную
сетку
в плоскости
с
шагами
и
.
Используем шаблон следующего вида:
m, n+1
m, n
m+1, n
m-1, n
m, n-1
Заменим в заданном уравнении производные разностными соотношениями, тогда получим:
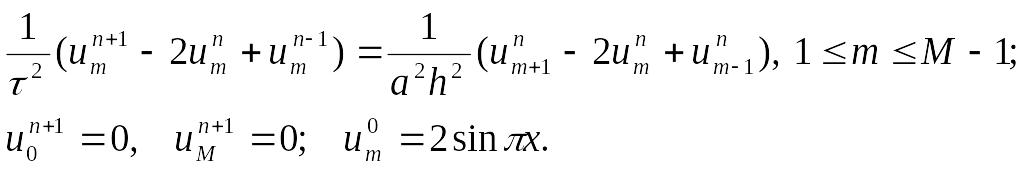
Для того чтобы начать
считать, необходимо знать
.
Для этого разложим в ряд Тейлора
:
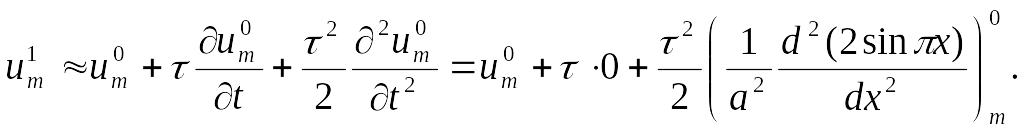
При известных
значениях
,
схема позволяет последовательно
вычислить все
.
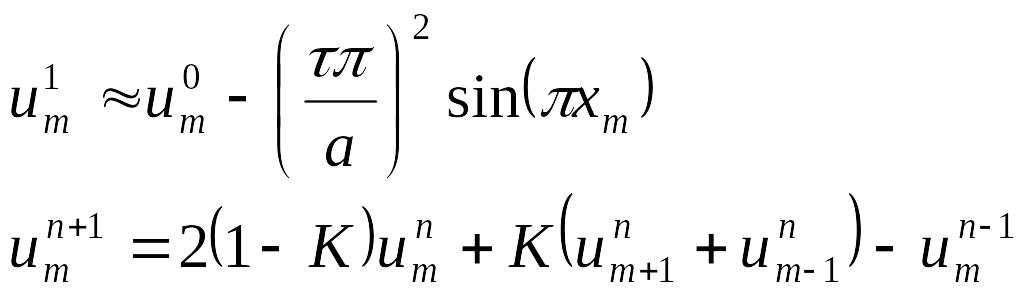
Выясним теперь порядок аппроксимации схемы:
Разложим в ряд Тейлора
функции из (1) в узле
:
Запишем невязку:
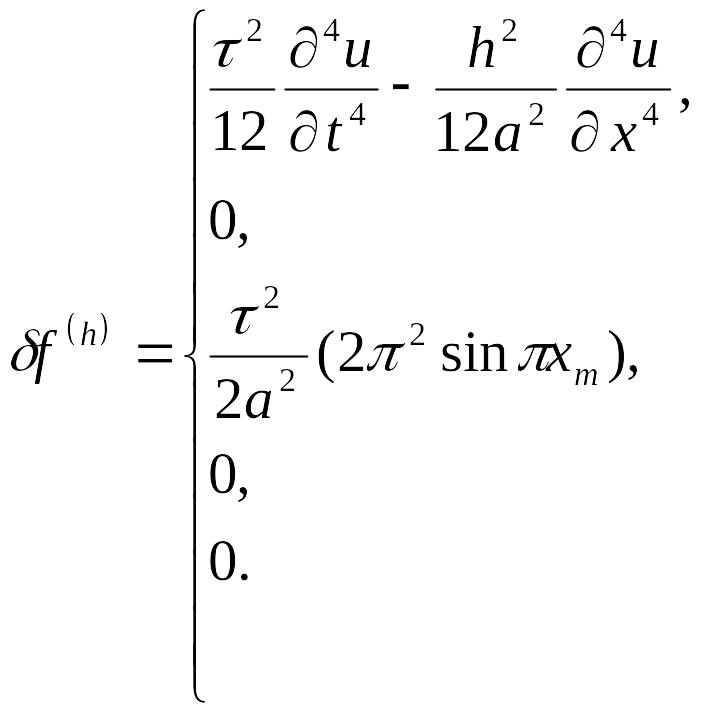
Отсюда видно, что схема
имеет порядок аппроксимации
.
Исследуем устойчивость схемы по начальным данным:
Воспользуемся методом разделения переменных.
Сделаем замену
,
тогда для множителя роста
получим уравнение:
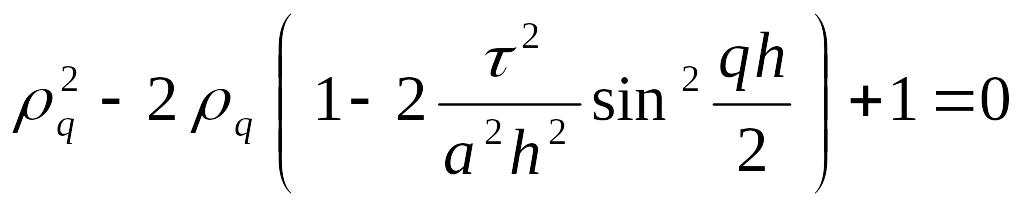
Пусть
,
тогда уравнение примет вид:
,
.
a)
при
<1:
получаем устойчивость.
б)
при |c|=1:
получаем устойчивость.
в)
при |c|>1,
то
>1
получаем неустойчивость.
Следовательно, для устойчивости необходимо выполнение неравенства:
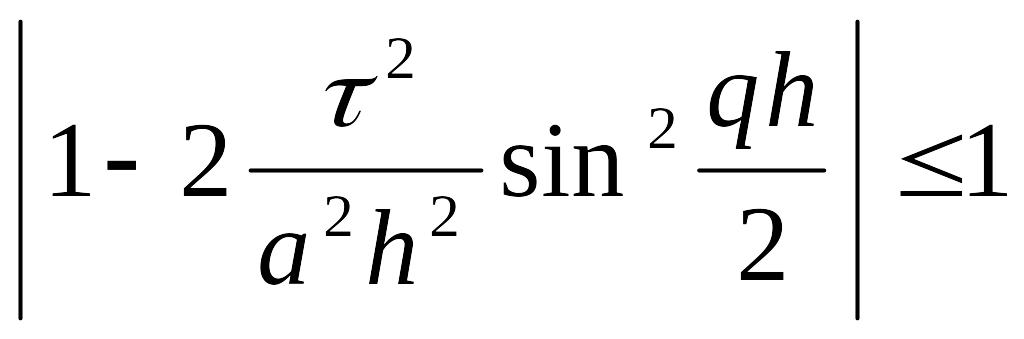
Из этого неравенства
получаем что, наша схема условно устойчива
при
.
Найдем точное решение нашего дифференциального уравнения с учетом начальных данных граничных условий:
Пусть
,
тогда исходное уравнение перепишется
в виде:
Получаем:
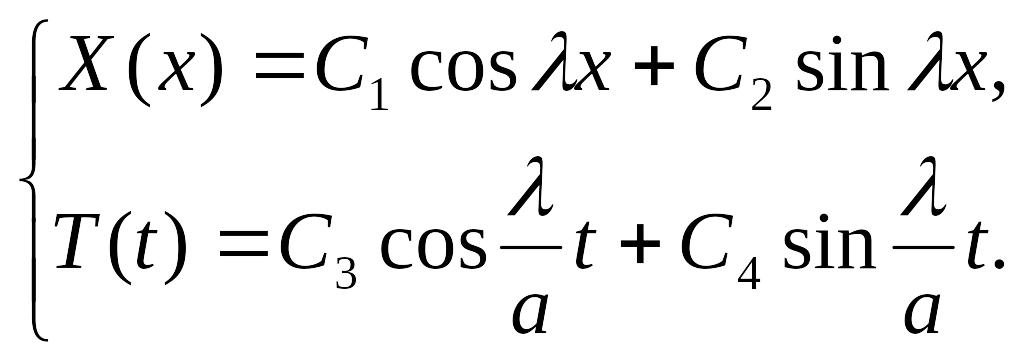
Используя граничные условия, получим систему:
,
,
.
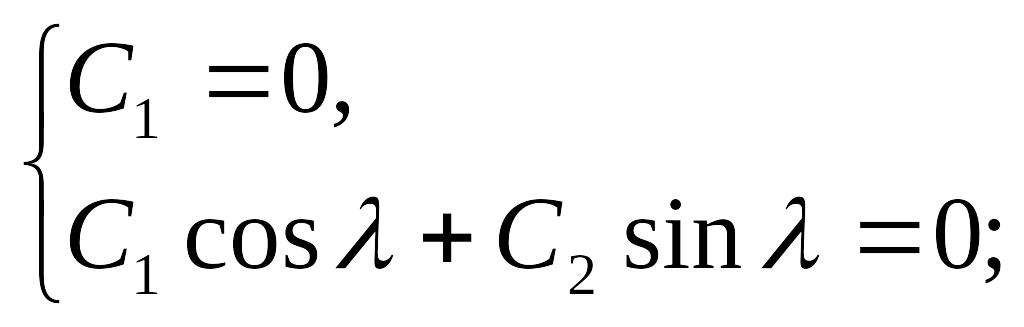
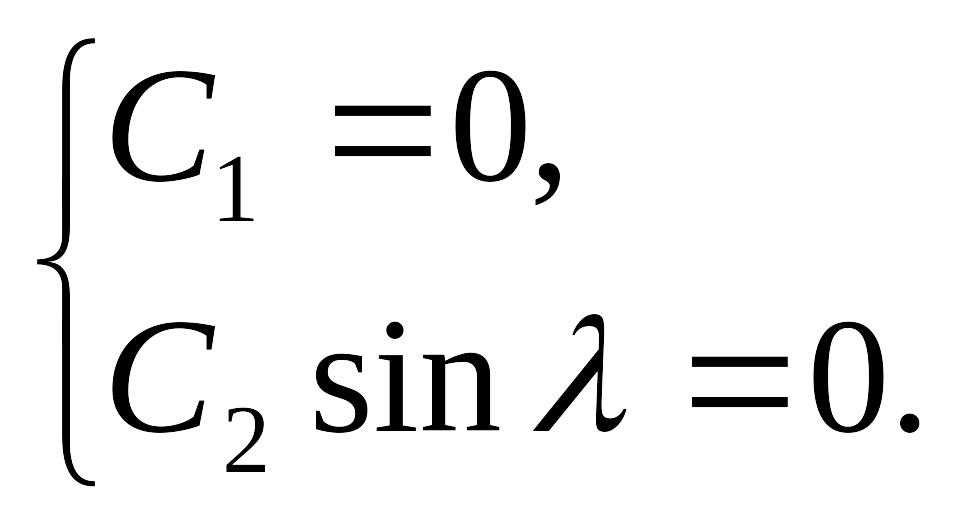
Общий вид решения:
.
Таким образом, получим:
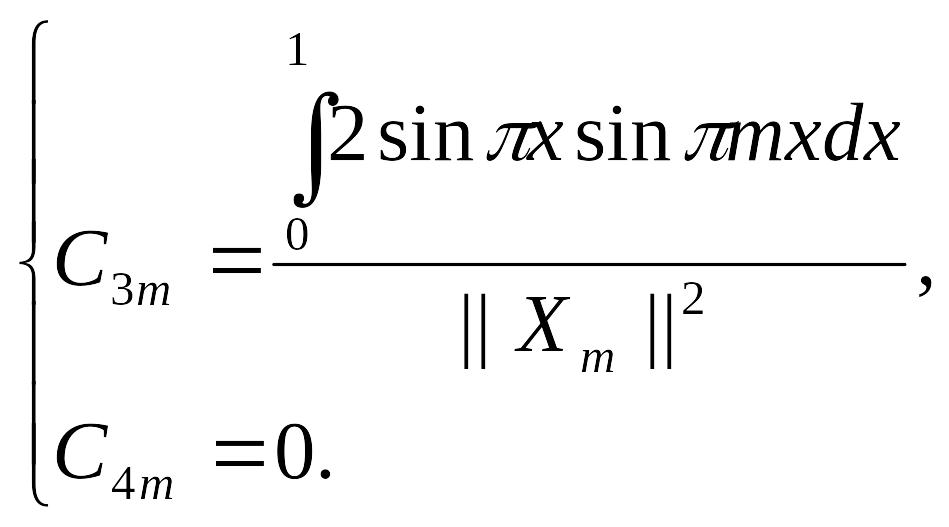
И с учётом нормы:
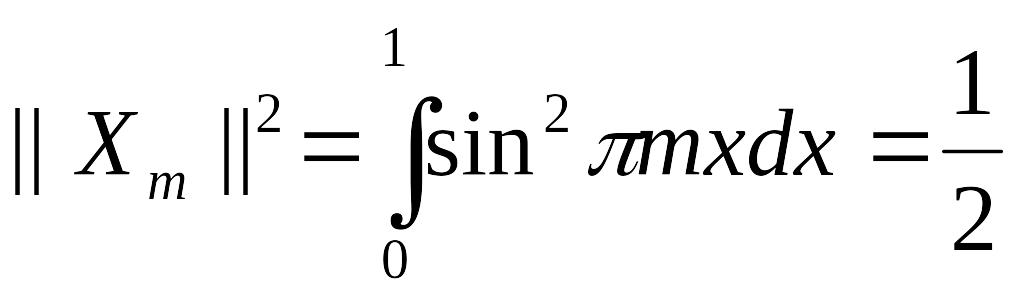
общее решение перепишется в следующем виде:
, 
График эталонной функции выглядит следующим образом:
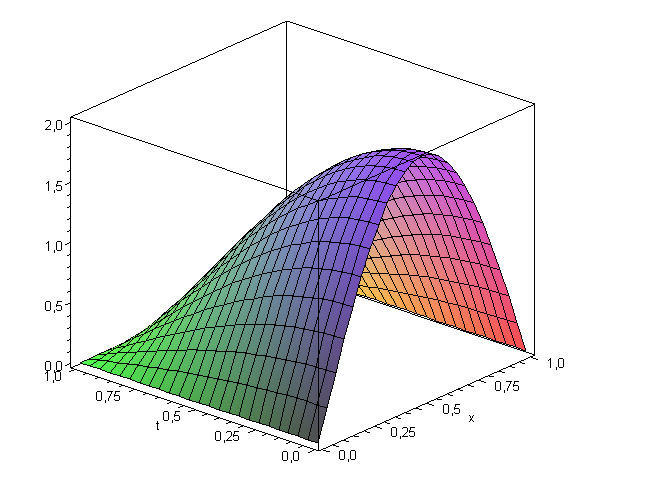
Полученные результаты занесем в таблицы:
,
xi |
Полученное решение |
Точное решение |
Погрешность |
0 |
0 |
0 |
0 |
0.1 |
0.5342604707 |
0.5342537975 |
6.6731698413e-6 |
0.2 |
1.0162238041 |
1.016211111 |
1.2693123368e-5 |
0.3 |
1.3987120711 |
1.3986946005 |
1.7470585556e-5 |
0.4 |
1.6442846552 |
1.6442641173 |
2.0537904944e-5 |
0.5 |
1.7289032009 |
1.728881606 |
2.1594831224e-5 |
0.6 |
1.6442846552 |
1.6442641173 |
2.0537904986e-5 |
0.7 |
1.3987120711 |
1.3986946005 |
1.7470585518e-5 |
0.8 |
1.0162238041 |
1.016211111 |
1.2693123347e-5 |
0.9 |
0.5342604707 |
0.5342537975 |
6.6731698277e-6 |
1 |
0 |
0 |
0 |
,
xi |
Полученное решение |
Точное решение |
Погрешность |
0 |
0 |
0 |
0 |
0.1 |
0.5342538645 |
0.5342537975 |
6.6976228452e-8 |
0.2 |
1.0162112384 |
1.016211111 |
1.2739631927e-7 |
0.3 |
1.3986947759 |
1.3986946005 |
1.7534550456e-7 |
0.4 |
1.6442643234 |
1.6442641173 |
2.0613010454e-7 |
0.5 |
1.7288818228 |
1.728881606 |
2.1673847339e-7 |
0.6 |
1.6442643234 |
1.6442641173 |
2.0613146767e-7 |
0.7 |
1.3986947759 |
1.3986946005 |
1.7534598018e-7 |
0.8 |
1.0162112384 |
1.016211111 |
1.2739641386e-7 |
0.9 |
0.5342538645 |
0.5342537975 |
6.6975921809e-8 |
1 |
0 |
0 |
0 |
В качестве дополнительного исследования посмотрим, что произойдет с нашим численным решением, если мы не удовлетворим требование условной устойчивости:
,
xi |
Полученное решение |
Точное решение |
Погрешность |
0 |
0 |
0 |
0 |
0.1 |
0.5342572314 |
0.5342537975 |
3.4338507826e-6 |
0.2 |
1.0162176426 |
1.016211111 |
6.5315723241e-6 |
0.3 |
1.3987035905 |
1.3986946005 |
8.98993806e-6 |
0.4 |
1.6442746856 |
1.6442641173 |
1.056830602e-5 |
0.5 |
1.7288927182 |
1.728881606 |
1.1112174555e-5 |
0.6 |
1.6442746856 |
1.6442641173 |
1.0568306023e-5 |
0.7 |
1.3987035905 |
1.3986946005 |
8.9899380591e-6 |
0.8 |
1.0162176426 |
1.016211111 |
6.531572325e-6 |
0.9 |
0.5342572314 |
0.5342537975 |
3.4338507815e-6 |
1 |
0 |
0 |
0 |
,
xi |
Полученное решение |
Точное решение |
Погрешность |
0 |
0 |
0 |
0 |
0.1 |
-3.4871180961e35 |
0.5342537975 |
-3.4871180961e35 |
0.2 |
4.753965566e37 |
1.016211111 |
4.753965566e37 |
0.3 |
1.9088069928e37 |
1.3986946005 |
1.9088069928e37 |
0.4 |
5.9716514983e37 |
1.6442641173 |
5.9716514983e37 |
0.5 |
-3.907452979e37 |
1.728881606 |
-3.907452979e37 |
0.6 |
5.0013264319e37 |
1.6442641173 |
5.0013264319e37 |
0.7 |
8.640863953e37 |
1.3986946005 |
8.640863953e37 |
0.8 |
7.4357107403e37 |
1.016211111 |
7.4357107403e37 |
0.9 |
-9.9937776523e35 |
0.5342537975 |
-9.9937776523e35 |
1 |
0 |
0 |
0 |
Численно порядок сходимости получился равным: р=1.99841
Вывод: достаточно простая лабораторная работа, в теории достаточно подробно описана данная разностная схема. Численные результаты полностью согласуются с аналитическими. Требование условной устойчивости, как можно убедиться из таблиц, вполне оправдано.
Задание №23