Разностная схема повышенной точности.
Для дифференциальной задачи:
методом
конечных разностей численно найти
решение при
.
Для решения использовать разностную схему:
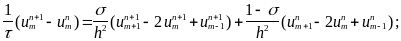
За счет подбора соотношения между (шаг по времени ) и h (шаг по пространству )
использовать при численном решении схему повышенной точности.
Полученное
численное решение сравнить с точным
решением в тех же точках по переменной
при
,
в которых получено численное решение.
Численно вычислить порядок сходимости.
Дополнительно:
сравнить с простейшей схемой
Решение:
Для начала найдем точное решение заданного дифференциального уравнения. Полностью искать решение мы не будем, запишем лишь конечный результат.
Выпишем общее решение исходного дифференциального уравнения:
Поскольку требуется подсчитать решение при , то, в силу малости последнего члена ряда, им можно пренебречь. Тогда получим, что решение выглядит следующим образом:
Исследуем аппроксимацию заданной схемы:
Данная схема построена на шеститочечном шаблоне:
Выясним порядок
аппроксимации схемы, разложив все
функции в ряд в точке
:
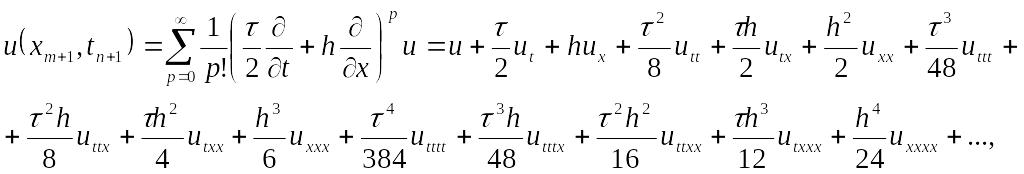
Разложения
для
получается из последнего выражения
путем замены
на
,
а разложение для
- заменой
на
и т. д. по аналогии.
Основные выкладки опустим в силу их очень большого объема. Приведем только последние шаги по нахождению выражения для невязки:
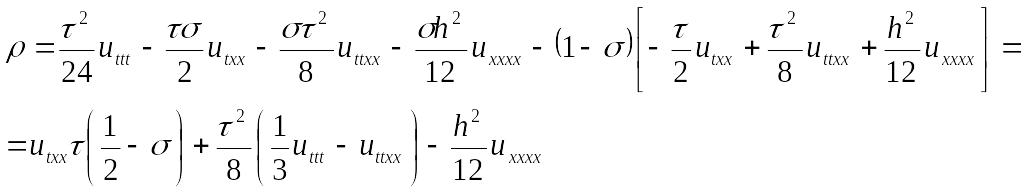
Поскольку в
случае моего варианта
,
то порядок аппроксимации в данном случае
будет
.
Найдем теперь соотношение между шагом по времени и по пространству так, чтобы порядок аппроксимации данной схемы был больше.
Для этого вспомним исходное дифференциальное уравнение и, используя его, запишем
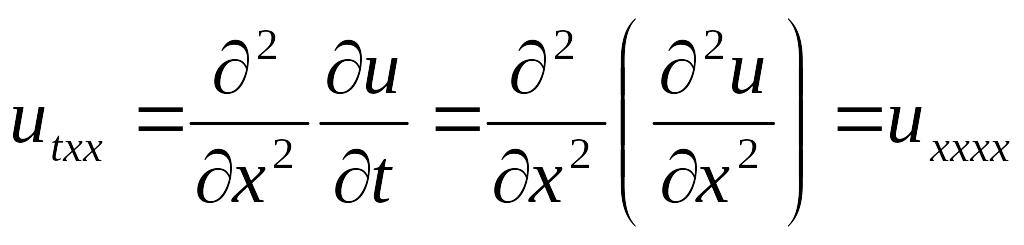
Тогда выражение для невязки перепишется следующим образом:
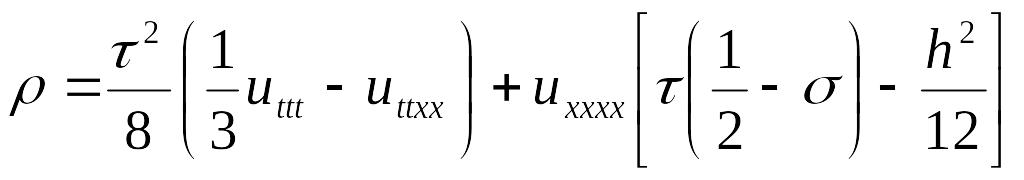
Положим
теперь, что
,
тогда получим, что порядок аппроксимации
будет
.
Окончательно, для шагов по времени и пространству, получим:
Исследуем устойчивость данной схемы с помощью принципа максимума.
Принцип максимума позволяет доказать устойчивость в схем для уравнения переноса, параболических и эллиптических уравнений. Пусть имеется схема вида
где на каждом
слое суммирование производится по узлам
шаблона около
узла. Будем считать, что
.
Пусть для коэффициентов этой схемы
выполнены неравенства
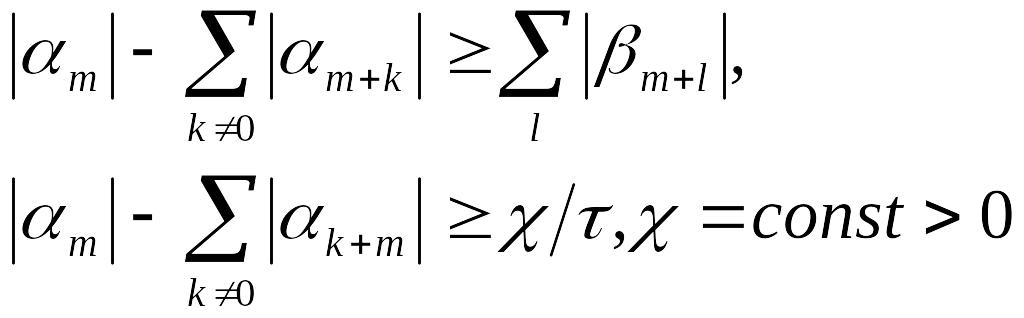
В нашем случае неравенство примет следующий вид:
Таким образом, схема устойчива при
Положим
например
,
тогда
(исходя из условий повышенной точности).
С помощью метода прогонки найдем численное решение:
Перепишем нашу схему в виде:
Ну а далее все по аналогии с другими работами.
Введем следующие обозначения:
;
;
;
Предположим
что: 
(1)
Если m
поменять на m-1, то
получим, что
.
Подставив последнее выражение в схему, получим:
(2)
Сравнивая это выражение с выражением (1), получаем:
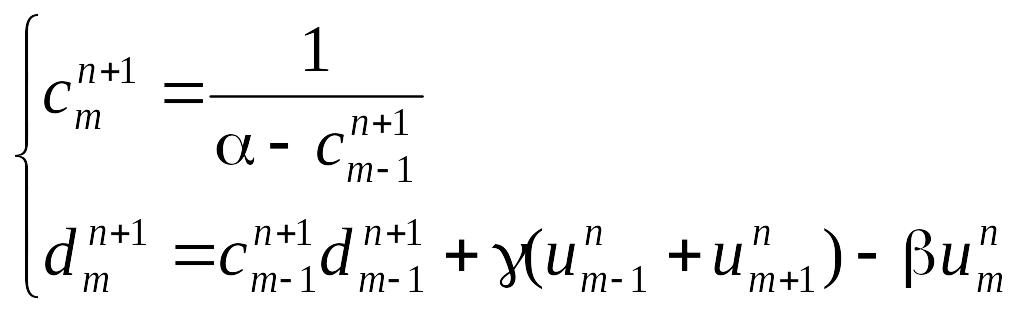
Теперь, подставив в (1) и исходную схему индекс m = 1, получим:
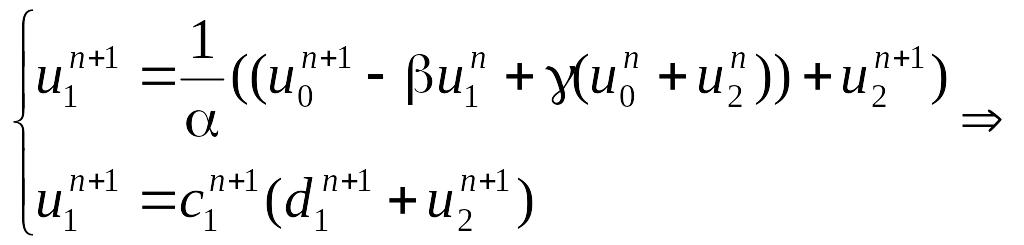
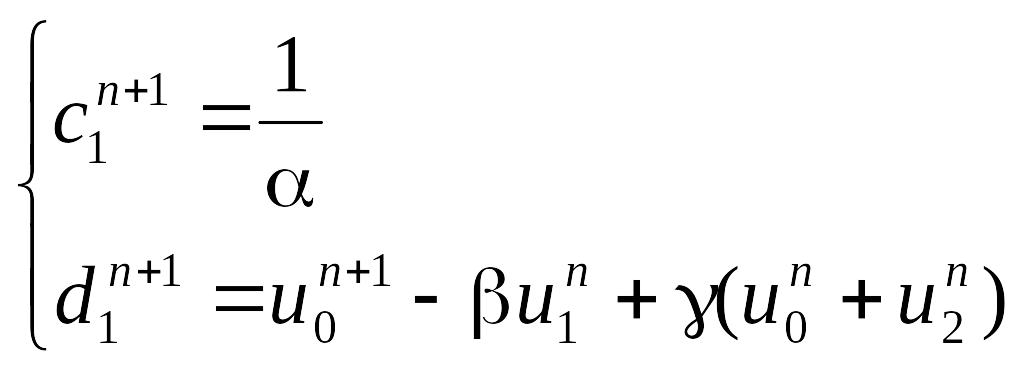
Теперь, когда все готово для счета, решение ищем по формуле (1).
Полученные результаты заносим в таблицу:
-
xi
Точное решение
Полученное решение
Погрешность
0
-4.473000000000001
-4.473000000000001
0
0.1
-4.174800000000001
-4.174799999999996
5.329070518200751e-15
0.2
-3.876600000000001
-3.876599999999992
8.881784197001252e-15
0.3
-3.578400000000001
-3.578399999999987
1.376676550535194e-14
0.4
-3.280200000000001
-3.280199999999985
1.554312234475219e-14
0.5
-2.982000000000001
-2.981999999999985
1.598721155460225e-14
0.6
-2.683800000000001
-2.683799999999984
1.687538997430238e-14
0.7
-2.385600000000001
-2.385599999999986
1.509903313490213e-14
0.8
-2.087400000000001
-2.087399999999989
1.154631945610163e-14
0.9
-1.789200000000001
-1.789199999999995
5.995204332975844e-15
1
-1.491000000000000
-1.491000000000000
0
Сравним с простейшей схемой
-
xi
Точное решение
Полученное решение
Погрешность
0
-4.473000000000001
-4.473000000000001
0
0.1
-4.174800000000001
-4.174799999999999
2.6645352591e-15
0.2
-3.876600000000001
-3.876599999999997
3.5527136788e-15
0.3
-3.578400000000001
-3.578399999999996
4.4408920985e-15
0.4
-3.280200000000001
-3.280199999999996
4.8849813084e-15
0.5
-2.982000000000001
-2.981999999999996
4.8849813084e-15
0.6
-2.683800000000001
-2.683799999999996
4.8849813084e-15
0.7
-2.385600000000001
-2.385599999999996
4.4408920985e-15
0.8
-2.087400000000001
-2.087399999999997
3.5527136788e-15
0.9
-1.789200000000001
-1.789199999999999
1.9984014443e-15
1
-1.491000000000000
-1.491000000000000
0
Попытаемся численно оценить порядок сходимости. Для тех значений переменных, в которых мы решали задачу, численно вычислить порядок сходимости не представляется возможным, так как для минимального шага мы уже получаем предельную погрешность.
Для того чтобы понять, почему это происходит нужно посмотреть на точное решение нашего уравнения. Видно, что с увеличением времени решение задачи выглаживается, и становится зависимым только от x.
Для наглядного представления посмотрим на график точного решения:
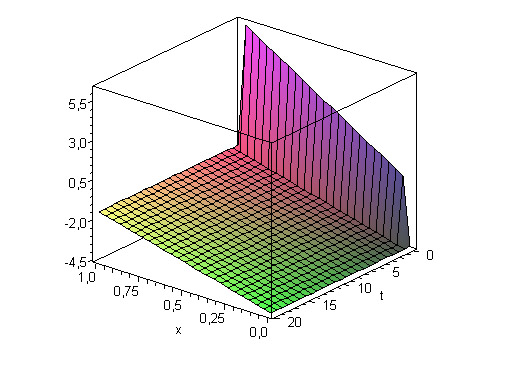
Из графика видно, что функция зависит от t только вблизи границы t=0. Более подробно построим этот участок графика:
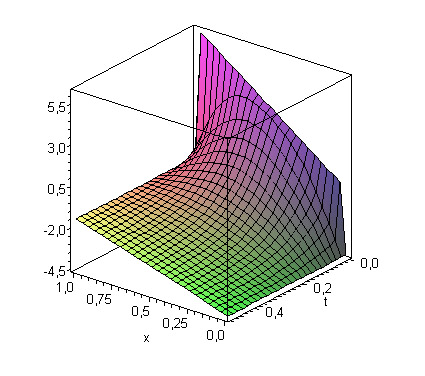
На этом графике достаточно хорошо видно,
что функция зависит от t
только в области
.
На остальном же участке функция линейная
от x, поэтому достигается
отличная точность при t=20.
Вследствие этого возникает следующее предположение: попробовать вычислить порядок сходимости в области, где функция изменяется в обоих переменных.
Для этого эталонное решение, естественно, программируем в виде ряда. Рассматриваем какую-либо точку, например точку (0.5,0.3)
В этом случае получаем порядок сходимости p=1.5 при изменении шага по h с 0.05 до 0.01 и соответствующим изменением шага по h. То, что порядок сходимости немного не сходится с порядком аппроксимации в данной работе не столь важный факт. Он, как мы смогли убедиться, очень сильно зависит от области решения.
Вывод: Возникли некоторые трудности при численном подсчете порядка сходимости, а в остальном все получилось достаточно хорошо. Затруднительным показался, пожалуй, лишь метод прогонки. Несмотря на это получены отличные результаты. При построении трехмерных графиков понимание поведения решения значительно упрощается.
Задание №22