Интегрирование обыкновенных дифференциальных уравнений. Разностная схема 4 порядка.

Для задачи:

на трехточечном шаблоне с постоянным шагом построить методом неопределенных коэффициентов устойчивую разностную схему 4 порядка точности.

По полученной разностной схеме численно проинтегрировать на интервале .

Сравнить полученные результаты с точным решением уравнения в точках .

Решение:

Рассмотрим заданное дифференциальное уравнение:

Обозначим правую часть уравнения следующим образом:

Согласно теории метод неопределенных коэффициентов заключается в выполнении следующего равенства: , тогда:

,

где , , ( )

Теперь для вычисления невязки разложим в ряд Тейлора функции:

Получим невязку:

Из этого выражения видно, что для того, чтобы разностная схема имела 4^ый порядок точности необходимо, чтобы выполнялись следующие условия:

Решая данную систему, получим:

Разностная схема будет иметь вид:

Или:

,

где .

Найдём точное решение заданного уравнения с начальными данными.

Найдём решение однородного уравнения, а затем частное решение неоднородного. Общее решение будет выглядеть следующим образом:

, где

Частное решение будем искать в виде:

Проделав необходимые вкладки, получим:

Тогда общее решение будет иметь вид:

В итоге решение имеет следующий вид:

Полученные результаты заносим в таблицы:

h=0.1

xi	Точное значение	Вычисленное значение	Погрешность
0.1	212.6433859525	212.6433692308	1.6721739826e-5
0.5	317.8861434623	317.8860667486	7.6713727083e-5
1	525.4647873014	525.4646496695	1.3763188554e-4

h=0.01

xi	Точное значение	Вычисленное значение	Погрешность
0.1	212.6433859525	212.6433859509	1.6464696273e-10
0.5	317.8861434623	317.886143455	7.3359842645e-9
1	525.4647873014	525.4647872884	1.29559794e-8

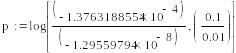
Необходимые расчеты мы провели, посмотрим теперь на некоторые дополнительные моменты. Можно увидеть, что дальнейшее уменьшение шага интегрирования вызывает уменьшение погрешности лишь в точках сетки, близких к левой границе отрезка. На правом конце, наоборот наблюдается увеличение погрешности, по сравнению с шагом h=0.01.

Рассчитать изменение временных затрат, связанных с уменьшением шага интегрирования, в данной лабораторной работе представляется затруднительным, так как среда Mathcad в связке с двуядерным процессором AMD x86 2.8 GHz выполняет расчет по разностной схеме практически мгновенно, а уменьшать шаг мы не можем из-за потери точности.

Если все же подойти к этому вопросу формально, например, нагрузить процессор WinRar-ом, уменьшить шаг, не обращая внимания на погрешность, и проводить расчет, то можно получить некоторые результаты. Так, при уменьшении шага в 10 раз, скорость расчета (по разностной схеме и построению 4-х таблиц) приблизительно увеличивается с 1 до 5 секунд, т.е. время на выполнение увеличивается приблизительно в 5 раз.

Вывод: Изученный метод так же дал совпадение практических результатов с теоретическими, это является наилучшей оценкой проделанной работы.

Задание №20