Интегрирование обыкновенных дифференциальных уравнений. Метод прогонки

Численно проинтегрировать дифференциальное уравнение:

с точностью на интервале . Параметр

Граничные условия:

Для решения подобрать устойчивую разностную схему 2 порядка точности (выбор схемы обосновать).

Численно вычислить порядок сходимости.

Решение:

Рассмотрим применение метода прогонки на примере разностного аналога граничной задачи для дифференциального уравнения второго порядка:

с двухточечными краевыми условиями

где известные функции и, в нашем случае:

Предположим, что функции p(x), q(x), f(x) непрерывны на данном отрезке.

Для решения задачи разностным методом разобьём отрезок на равных частей и введём обозначения:

Для внутренних узлов сетки будем использовать разностное уравнение:

где

Перепишем разностное уравнение в виде:

Пусть:

Отсюда будем иметь:

Предположим, что:

, отсюда

Тогда уравнение примет вид:

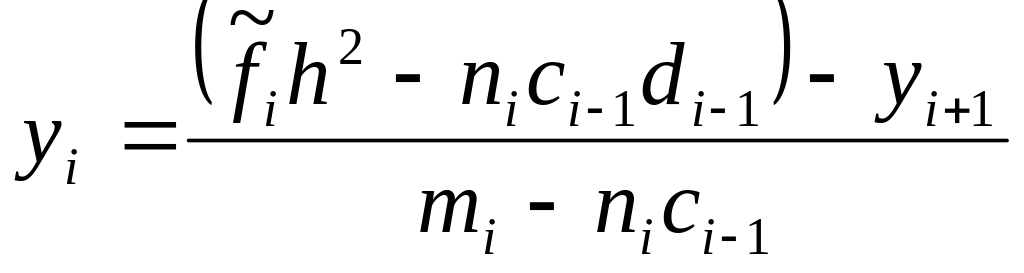
Для определения и получим рекуррентные формулы:

Пользуясь трехчленными формулами, из первого краевого условия и уравнения получаем:

Исключая из этих двух уравнений значение , находим:

где

С другой стороны имеем

Тогда:

По известным значениям и последовательно определяются коэффициенты и до и включительно. Это прямой ход прогонки.

Обратный ход начинается с определения .

Используя второе краевое условие и формулы (2), взятые при и , получим систему трёх уравнений

Решая эту систему относительно , будем иметь

Теперь по формулам последовательно находим . Это обратный ход метода прогонки.

Исследуем аппроксимацию полученной разностной схемы:

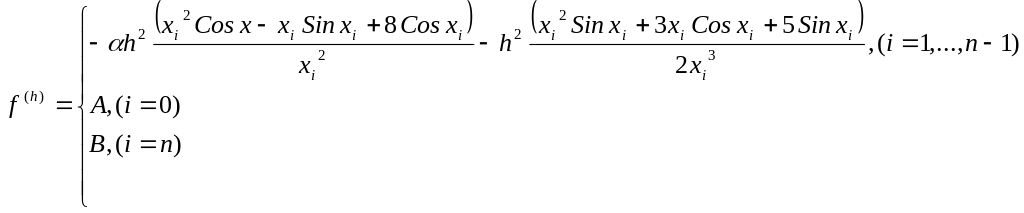
Для этого, как обычно, напишем четыре члена ряда Тейлора для всех функций из разностной схемы:

,

,

,

,

,

.

Где , , и , , .

Подставим эти выражения:

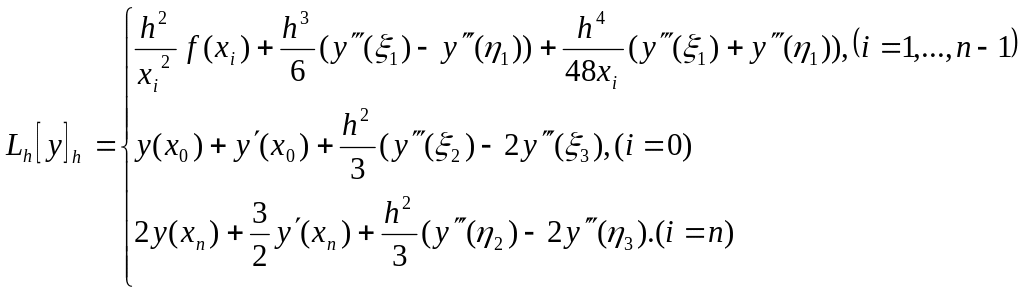
Получим невязку для нашей разностной схемы:

Заключаем, что схема имеет второй порядок аппроксимации.

Полученные результаты заносим в итоговую таблицу:

5. Шаг h=0.01

xi	Точное значение	Вычисленное значение	Погрешность
1	2.1887225213	2.1851375953	3.5849260401e-3
1.01	2.2580538321	2.2545270768	3.5267552804e-3
1.02	2.3287442374	2.3252736205	3.470616952e-3
…	…	…	…
1.98	24.9741539576	24.970804948	3.3490095706e-3
1.99	25.481247787	25.4778591309	3.3886561336e-3
2	25.9963614221	25.9929322717	3.4291504553e-3

6. Шаг h=0.001

xi	Точное значение	Вычисленное значение	Погрешность
1	2.1887225213	2.1886864535	3.6067828296e-5
1.001	2.1955963596	2.1955603507	3.6008898701e-5
1.002	2.2024831985	2.2024472483	3.5950180365e-5
…	…	…	…
1.998	25.8926931278	25.8926572524	3.5875379549e-5
1.999	25.9444868023	25.9444508828	3.591942215e-5
2	25.9963614221	25.9963254586	3.5963554893e-5

Порядок сходимости p=1.9973602

Вывод: Порядок сходимости полностью совпал с теоретическим значением. При наличии под рукой справочника, с формулами для коэффициентов по данной теме, метод прогонки становится хорошим инструментом для решения ОДУ.

Задание №19