Исследование аппроксимации и устойчивости разностной схемы системы обыкновенных дифференциальных уравнений

Исследовать во внутренних узлах устойчивость разностной схемы:

N - натуральное число,

для дифференциальной задачи

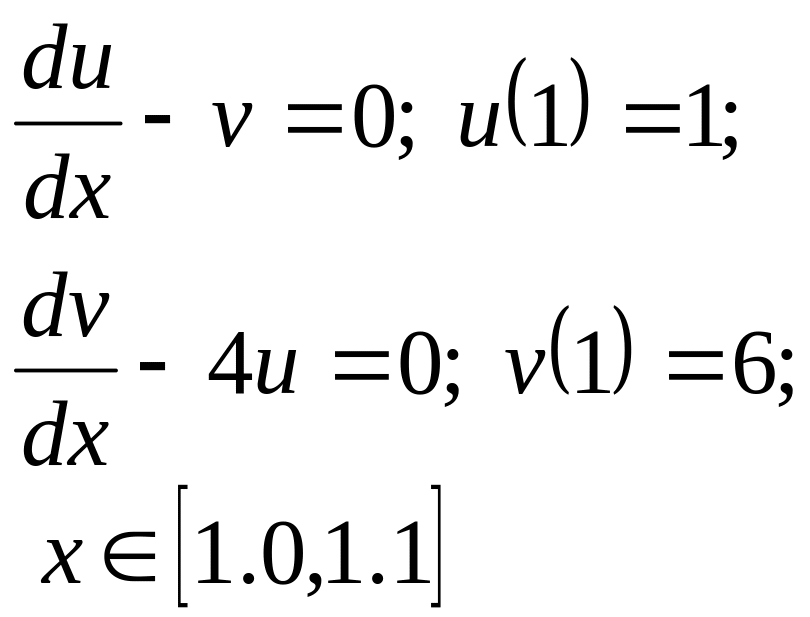
Для доказательства устойчивости необходимо построить оператор перехода (матрицу 4х4) (см. /7/).

Подобрать параметры таким образом, чтобы аппроксимация схемы во внутренних узлах была 2 порядка,

Решить систему любым методом на отрезке с шагом, равным 0,01.

Решение.

1. Исследуем порядок аппроксимации разностной схемы:

Разложим в ряд Тейлора в окрестности точки x= все функции из этой схемы, взяв четыре члена:

,

,

,

.

Где , .

Подставим эти выражения, положив и (т. к. и , то и ). Получим:

Т. к. и , то

Найдём невязку:

Пусть и принадлежат линейному нормированному пространству , которое состоит из элементов: , тогда . Если же положить, что третьи производные ограничены:

, ,

, .

то получим:

,

где .

Т. е. при и разностная схема имеет второй порядок аппроксимации.

2. Исследуем устойчивость разностной схемы с использованием спектрального признака.

Для этого перепишем исходную разностную схему в следующем виде:

В первое уравнение данной системы подставим значение из второго, а во второе из первого и получим:

Добавим к этой системе уравнения: , и запишем следующее соотношение:

.

Введём норму . Если выполняется , где , тогда и схема устойчива. Распишем все :

.

.

С учётом этого схема устойчива.

3. Для расчета дифференциальной задачи по заданной разностной схеме было принято решение воспользоваться языком программирования Fortran. Это сделано в силу простоты задания цикла для решения системы уравнений.

Полученные результаты занесем в таблицы:

1. Шаг h=0.1

i	Точное значение U	Точное значение V	Вычисленное значение U	Вычисленное значение V	Погр. U	Погр. V
1	1.42274	4.48294	1.40000	4.40000	“0.02274”	“0.08294”
2	1.90258	5.14579	1.89648	5.12965	0.00610	0.01614
3	2.45877	6.01517	2.42900	5.92079	0.02977	0.09438
…	…	…	…	…	…	…
88	6.60198e7	1.3204e8	66444144.0	132557304.0	4.24442e5	5.17723e5
89	8.06368e7	1.61274e8	81168664.0	161932992.0	5.3191e5	6.59484e5
90	9.849e7	1.9698e8	99156232.0	197818544.0	6.66278e5	8.38637e5

2. Шаг h=0.01

i	Точное значение U	Точное значение V	Вычисленное значение U	Вычисленное значение V	Погр. U	Погр. V
1	1.0402	4.0408	1.40000	4.40000	“0.02274”	“0.08294”
2	1.08082	4.08322	1.08082	4.08321	0.0	0.00001
3	1.12187	4.12727	1.12166	4.12647	0.00021	0.00080
…	…	…	…	…	…	…
898	9.46281e7	1.89256e8	94634320.0	189263888.0	6.21262e3	7.67323e3
899	9.65397e7	1.93079e8	96546072.0	193087328.0	6.35004e3	7.88409e3
900	9.84900e7	1.96980e8	98496456.0	196987952.0	6.50229e3	8.04459e3

Порядок сходимости:

Для U(x): p=2.01059

Для V(x): p=2.01807

“ ” – погрешность связанная с начальным приближением.

Воспользуемся двухточечной схемой из дополнительного задания и аналогично решим дифференциальную задачу:

3. Шаг h=0.1

   i	Точное значение U	Точное значение V	Вычисленное значение U	Вычисленное значение V	Погр. U	Погр. V
   1	1.42274	4.48294	1.40000	4.40000	0.02274	0.08294
   2	1.90258	5.14579	1.84000	4.96000	0.06258	0.18579
   3	2.45877	6.01517	2.33600	5.69600	0.12277	0.31917
   …	…	…	…	…	…	…
   88	6.60198e7	1.3204e8	13932877.0	27865754.0	5.20900e7	1.04174e8
   89	8.06368e7	1.61274e8	16719452.0	33438904.0	6.39173e7	1.27835e8
   90	9.849e7	1.9698e8	20063342.0	40126684.0	7.84266e7	1.56853e8

4. Шаг h=0.01

i	Точное значение U	Точное значение V	Вычисленное значение U	Вычисленное значение V	Погр. U	Погр. V
1	1.0402	4.0408	1.04000	4.04000	0.0002	0.0008
2	1.08082	4.08322	1.08040	4.08160	0.00042	0.00162
3	1.12187	4.12727	1.12122	4.12482	0.00065	0.00245
…	…	…			…	…
898	9.46281e7	1.89256e8	79258376.0	158516752.0	1.53697e7	3.07395e7
899	9.65397e7	1.93079e8	80843544.0	161687088.0	1.56962e7	3.13924e7
900	9.84900e7	1.96980e8	82460416.0	164920832.0	1.60295e7	3.20591e7

Порядок сходимости:

Для U(x): p=0.68954

Для V(x): p=0.68954

Вывод: Одна из самых интересных лабораторных работ. Для меня решить задачу с использованием языка программирования показалось несколько проще, чем изучать построение циклов в среде MathCad. Результаты говорят сами за себя. Порядок сходимости совпал с теоретическим, ему не помешала ни быстро растущая функция, ни тип данных REAL*4 используемый по умолчанию при написании программы.

Задание №18