Интегрирование обыкновенных дифференциальных уравнений с помощью интерполяционой ( неявной) формулы Милна /1,10,22/.

Для задачи:

,

, где - параметр,

на трех точечном шаблоне с постоянным шагом интегроинтерполяционным методом построить устойчивую разностную схему 4 порядка аппроксимации. Исследовать полученную схему на сходимость к исходной дифференциальной задаче. Используя построенную схему, проинтегрировать заданное дифференциальное уравнение с точностью на интервале . Численно вычислить порядок сходимости.

Дополнительно: сравнить с простейшей двухточечной схемой:

Решение:

Пусть дано дифференциальное уравнение с начальным условием:

Выбрав шаг h : , и положим:

В данной лабораторной работе воспользуемся так называемым методом предиктор-корректор. В качестве предиктора выбирается какая-либо явная формула, а в качестве корректора неявная формула. Остановимся на методе Милна, подробно описанном в книге Демидовича-Марона.

Первые четыре значения искомого решения для заданного уравнения с начальными данными определим по формуле Рунге-Кутты 4-ой степени точности (в дальнейших заданиях можно будет увидеть, что для получения лучших результатов степени точности предиктора и корректора должны совпадать), которая имеет следующий вид:

Где:

Дальнейшие значения определяются по следующей схеме:

• Вычисляем первое приближение 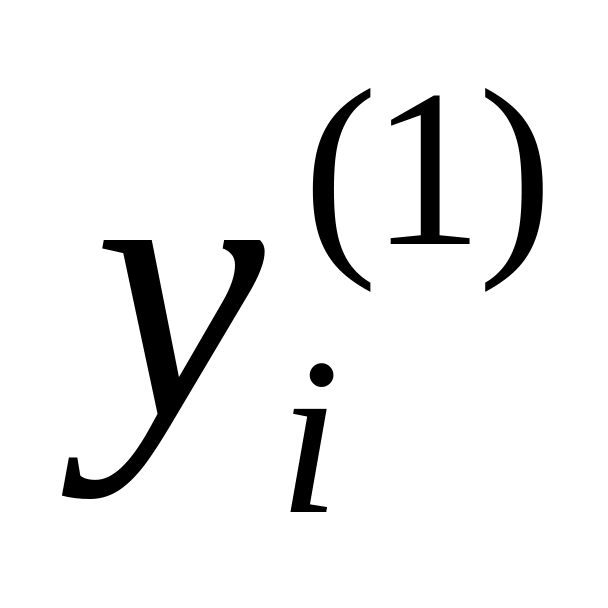для ближайшего следующего значения по формуле:

• Находим второе приближение по формуле:

• Последующие приближения находим по неявной формуле Милна:

Милн показал, что абсолютная погрешность значения приближенно равна:

.

В названии нашей лабораторной работы фигурирует только формула Милна, поэтому для вычисления будем пользоваться формулой:

для которой значения y_i получены с помощью формулы Рунге-Кутты.

Найдем порядок аппроксимации последней формулы:

Для этого разложим все функции этой формулы в ряд Тейлора в окрестности точки и для невязки получим следующее выражение:

, где - порядок аппроксимации формулы. Следовательно, формула имеет четвёртый порядок аппроксимации.

Теперь исследуем устойчивость данной разностной схемы:

Видим, что в правую часть y входит в виде линейной функции. В силу этого можем записать:

Приведём эту схему к каноническому виду:

Чтобы это сделать введём ещё одно уравнение и положим

;

Найдём собственные числа матрицы , тогда если , то схема устойчива.

;

При достаточно малых , . Следовательно, схема устойчива.

Теперь приступим к вычислениям:

Для задачи:

,

, где - параметр,

эталонным решением является следующая функция:

(Получено с помощью Maple12)

График функции выглядит следующим образом:

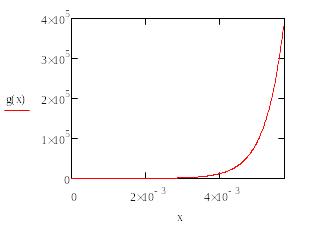
Как видно из графика функция достаточно быстро возрастает.

Теперь заполним следующую табличку, в которой укажем погрешность в точке 0.005 (эталонное значение функции = 9.3087423e4) в зависимости от различного шага и количества итераций:

Кол-во итераций	0	1	2	3
Шаг h
0.001	2.4664e3	1.6368485e3	1.08077e3	708.0120104
0.0001	8.6497	8.1311013	8.0963379	8.0940076
0.00001	1.22705e-3	1.2189575e-3	1.2189033e-3	1.2189029e-3
0.000001	1.26834e-7	1.2676173e-7	1.2676173e-7	1.2676173e-7
0.0000001	6.54836e-10	6.5483619e-10	6.5483619e-10	6.5483619e-10

На следующем этапе нам необходимо выбрать шаг h . После подбора по предыдущей табличке останавливаемся на шаге h=0.000001. Получим 5725 точек, в которых будем приближать решение уравнения:

xi	Точное решение
0	4	4	0	4	0
1e-6	4.0080521	4.0080521	0	4.0080521	0
2e-6	4.0161204	4.0161204	2.6645353e-15	4.0161204	-1.7763568e-15
…	…	…	…
5.723e-3	3.9841417e5	3.9921618e5	6.2276376e-7	3.9841417e5	6.2055187e-7
5.724e-3	3.9921618e5	4.0001981e5	6.2398612e-7	3.9921618e5	6.2241452e-7
5.725e-3	4.0001981e5	4.0082506e5	6.2584877e-7	4.0001981e5	6.2357867e-7

При этом разность между первой и второй итерацией составила величину порядка 10¹⁰. Видно, что для данного шага, уже нулевого приближения достаточно для нужной точности.

Вычислим порядок сходимости:

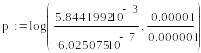
Дополнительное задание: сравнить с простейшей двухточечной схемой:

xi	Точное решение
0.00	4	4	0
1.00e-5	4.0812543	4.08044	8.1427339e-4
2.00e-5	4.1641591	4.1624976	1.6614626e-3
…	…	…	…
5.68e-3	3.6540966e5	3.2625621e5	3.9153453e4
5.69e-3	3.7283243e5	3.3281722e5	4.0015215e4
5.70e-3	3.8040599e5	3.3951017e5	4.0895818e4

Вывод: Хорошая лабораторная работа, расставляет многие вещи на свои места. Не смотря на большой рост функции, нужный результат достигнут. Порядок сходимости совпадает с теоретическим. Погрешность при переходе от итерации к итерации совпадает с выведенной Милном зависимостью.

Задание № 16