§2.2. Задача с подвижными концами и нефиксированным временем.

Рассматривается задача Больца при наличии ограничения в виде уравнений связи (описание объекта управления в пространстве состояний) и ограничения на управление в форме включения[9]:

(2.14)

Граничные условия:

Критерий оптимизации: (2.15)

Требуется определить оптимальное управление , которое минимизирует функционал (2.15) и удовлетворяет уравнению связи и граничным условиям. На основании принципа Лагранжа переходим к задаче на безусловный экстремум функционала:

(2.16)

Дальше, как в случае задачи с закрепленными концами, задача (2.16) разбивается на две. Первая задача имеет вид:

Необходимые условия оптимальности для этой задачи содержат сопряженную систему уравнений для определения , условия трансверсальности и условия стационарности по времени. Необходимые условия по второй задаче имеют вид принципа максимума.

Теорема (при подвижных концах и нефиксированном времени).

Для того, чтобы допустимые для задачи (2.15), (2.14) были её решением, необходимо:

1)Существование не обращающихся одновременно в ноль константы и множителей , которые являются решением сопряженной системы при и , что при любом , кроме точек разрыва , функция при , достигнет максимума:

1. выполнение условия трансверсальности и стационарности по времени:

(2.17)

§ 2.3. Задача быстродействия для траектории с закреплёнными концами.

Во многих задачах автоматического управления возникает необходимость минимизации времени перехода объекта из начального состояния в конечное. Такие оптимизационные задачи называются задачами быстродействия. Важность и распространённость задач быстродействия позволяют уделить им особое внимание и отдельно сформулировать теорему принципа максимума. Критерий оптимизации в этом случае имеет вид:

(2.18)

и, следовательно, интегрант . При описании объекта в виде (2.1) функция гамильтониан формируется:

(2.19)

Соотношения (2.11) для гамильтониана (2.19) остаются справедливыми. Тогда основная теорема принципа максимума для оптимальности по быстродействию и задачи с закрепленными концами формулируется следующим образом[8][10].

Теорема. Пусть - некоторое допустимое управление, переводящее объект из состояния , в состояние , а - соответствующая этому управлению фазовая траектория. Для оптимальности по быстродействию управления и траектории необходимо существование такой ненулевой непрерывной вектор - функции , удовлетворяющей системе уравнений (2.7), что:

1. для любого , являющегося точкой непрерывности управлен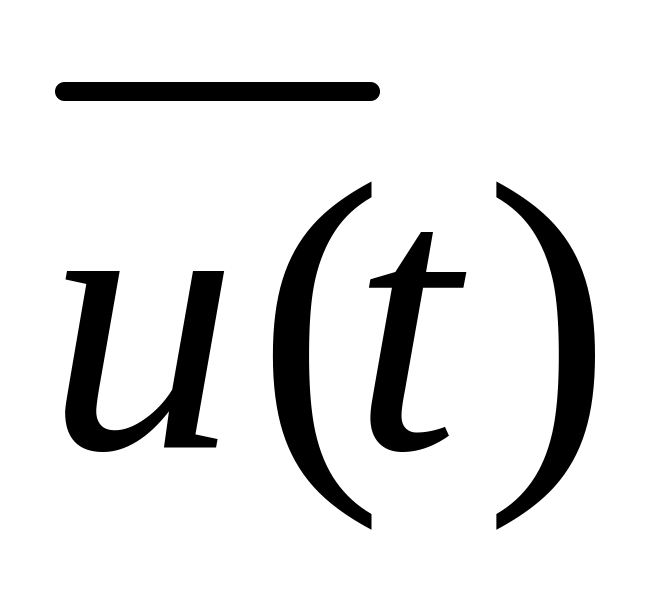ия , функция достигнет по максимума

(2.20)

2. в конечный момент времени выполняется соотношение:

(2.21).

В рассматриваемой задаче быстродействия интегрант не содержит в качестве переменной управляющее воздействие и максимизация гамильтониана осуществляется по функции , входящей в . Это обстоятельство позволяет сделать очень важный вывод. Если в функция входит линейно

,

где В – матрица числовых коэффициентов, оптимальное управляющее воздействие имеет вид кусочно-постоянной функции с конечным числом интервалов переключения. Функция гамильтониан в этом случае имеет вид:

Управляющее воздействие содержится только во втором слагаемом и, следовательно, максимальное значение определяется значением . Если множество – замкнутое, ограничение на составляющие вектора можно представить , и оптимальное значение

(2.22)

Из выражения (2.22) следует, что для всех оптимальное по модулю равно максимально допустимому значению , а по знаку зависит от знака суммы составляющих вектора . Число переключений для равно числу смены знака этой суммы. В задачах быстродействия для линейных систем число переключений функции определяется числом переменных состояния или (что равно) степенью дифференциального уравнения, описывающего динамику объекта оптимизации. Этот факт утверждается теоремой об – интервалах[8]. Пусть описание динамических свойств объекта имеет вид:

(2.23)

где A и B – матрицы с постоянными коэффициентами. Тогда теорема об интервалах формулируется следующим образом:

Теорема. Если характеристические числа матрицы A – действительные числа и область управления является замкнутой, тогда каждое из управлений является кусочно-постоянной функцией и имеет не более n-1 переключении (т.е. не более n интервалов постоянства), где n – порядок системы.

Гамильтониан для объекта управления

(2.23)

Так как от управлений первое слагаемое не зависит условие максимизации гамильтониана приобретает следующую форму:

Это условие выполняется, если каждое слагаемое по индексу j примет максимальное значение по модулю и со знаком, определяемым знаком суммы составляющих . Таким образом:

(2.24)

Для определения моментов смены знака для необходимо знать функции , которые для объекта управления с описанием (2.23) имеют математическое представление согласно (2.7)

(2.25)

Система уравнений (2.25) является сопряженной относительно (2.23) при (свободное движение):

(2.26)

Корни характеристического уравнения (2.25) равны корням характеристического уравнения (2.26) и имеют противоположный знак. Согласно теореме, корни (2.26) действительные и отрицательные , тогда

И оптимальное значение составляющих управления:

(2.27)

Функция, представляющая собой сумму экспонент с постоянными коэффициентами на полубесконечном интервале , может переходить через ноль не более (n-1) раз и имеет, следовательно, не более n интервалов постоянства. При комплексных корнях характеристического уравнения системы (2.26) число интервалов постоянства может быть больше и зависит от начальных условий системы (2.22).

Пример 1. Задача об оптимальной по быстродействию встрече движущихся объектов.[5] Объект A движется равномерно и прямолинейно. Изменение его координаты соответствует уравнению:

По той же прямой в пространстве за ним движется объект B, изменение координаты которого описывается уравнением второго порядка:

Управление имеет ограничение . Требуется определить такое управление , чтобы за минимальное время положение и скорости объектов A и B в пространстве совпали.

На практике подобная задача возникает, например, при заправке в воздухе самолетов, когда заправщик движется с постоянной скоростью и на параллельный курс к нему пристраивается заправляемый самолет. Управляющим воздействием при этом является тяга p двигателя самолета, заходящего на заправку. Предельные значения тяги и положительны. Для того чтобы записать ограничение на управление в принятом выше виде, его значение через представляется следующим образом:

Решение задачи удобнее провести относительно рассогласования между координатами объектов:

Относительно x процесс сближения двух объектов описывается уравнением:

Начальные условия для x:

В задачах быстродействия критерий оптимизации имеет вид:

Для решения задачи принципом максимума представим описание процесса сближения в форме пространства состояний:

(1П)

Составим гамильтониан:

В выражении для от управления зависит только последнее слагаемое, поэтому максимальное значение определяется его максимальным значением, что позволяет записать оптимальный закон управления с учетом ограничения на в виде

Уравнение для вектора :

На основании выражения для можно записать закон оптимального управления

При всех возможных сочетаниях знаков и функция и, следовательно, не более одного раза меняет знак и, таким образом, содержит не более двух интервалов постоянства. Из физического смысла задачи ясно, что в начале движения должно обеспечить разгон объекта В, а затем его торможение, поэтому на первом интервале следует принять , а на втором . Момент переключения и окончание процесса сближения составляют неизвестные параметры. Для их определения используем граничные условия и физические особенности протекания процесса движения. Так для согласно условию задачи движения объектов характеризуется тем, что и , что позволяет определить граничные условия для и в момент времени :

и

Система уравнений связи (1П) решается последовательно для и . На первом этапе решение системы имеет вид:

На втором этапе начальные значения и определяются как результат движения объектов на первом этапе, что позволяет найти постоянные интегрирования и определить и , приравняв их к нулю:

Из двух последних уравнений можно получить два соотношения для определения и :

Пример 2. Требуется определить экстремаль, которая минимизирует функционал

При условиях:

Имеем задачу с одним закрепленным концом и заданным временем движения объекта. В связи с тем, что имеется ограничение на скорость, задачу нельзя решить методом вариационного исчисления. Для решения на основе принципа максимума приведем задачу к виду задач оптимального управления:

(I-II)

Составим функцию Лагранжа и гамильтониан

Условие стационарности по x (уравнение сопряженного состояния) имеет вид:

Условие трансверсальности: Условие оптимальности по управлению:

Если , то , что недопустимо. Принимаем , тогда оптимальное управление с учетом ограничения имеет вид:

Определяем уравнение для сопряженного состояния

Оптимальная траектория определяется из уравнения связи:

Постоянные и определяются из краевых условий: